目的関数:機械学習の目標設定

AIを知りたい
先生、「目的関数」って一体何ですか?難しそうでよくわからないです。

AIエンジニア
そうだね、少し難しいかもしれないね。簡単に言うと、AIが学習する時の「目標」みたいなものだよ。AIは、この「目的関数」の値が良くなるように、一生懸命勉強するんだ。

AIを知りたい
目標、ですか?もう少し具体的に教えて下さい。

AIエンジニア
例えば、猫を判別するAIを考えてみよう。目的関数は「どれだけ正確に猫を判別できたか」を表す数値になる。AIは、この数値が大きくなるように、つまり猫をより正確に判別できるように学習していくんだよ。
目的関数とは。
人工知能の分野でよく使われる「目的関数」という言葉について説明します。この言葉は、機械学習の際に、学習の良し悪しを測るための計算方法を指します。この良し悪しを測るための計算結果を「損失」と言い、この損失をなるべく小さく、あるいは大きくすることで、機械学習のモデルをより良いものへと調整していきます。
目的関数の定義

機械学習は、大量の情報から隠れた規則や繋がりを学ぶ技術です。この学習を導く羅針盤の役割を果たすのが目的関数です。目的関数は、機械学習で作られた予測模型の正確さを数値で測るためのものです。この数値は、模型が目指す目標にどれくらい近づいているかを示す指標であり、いわば模型の成績表のようなものです。
目的関数の種類は様々ですが、基本的には数値が小さいほど良いとされる場合と、大きいほど良いとされる場合があります。例えば、誤差を評価する場合、目的関数の値は誤差の大きさを表し、この値が小さければ小さいほど、模型の予測は正確であると判断できます。逆に、正解率を評価する場合、目的関数の値は正解率を表し、この値が大きければ大きいほど、模型の性能が高いと判断できます。
機械学習の過程では、この目的関数の値を最小化、あるいは最大化するように、模型の内部設定である変数を調整していきます。ちょうど、職人が道具を微調整して最高の作品を作り上げるように、変数を少しずつ変えて、目的関数の値が最適な値になるように調整していくのです。この調整作業こそが機械学習の中心的な作業であり、最適な変数を見つけることで、情報に隠された真の関係性を捉え、高い精度で予測や分類を行う模型を作り上げることができるのです。目的関数は、機械学習の目指す方向を示す灯台のような存在であり、その光を頼りに、私たちは情報の海を航行し、未知の宝物を発見することができるのです。
損失関数との関係

学習済みモデルの良し悪しを測る指標は、目的関数と損失関数と呼ばれる二つの考え方があります。この二つは、よく似たものとして扱われがちですが、実際には異なるものです。それぞれが何を表し、どのように関係しているのか詳しく見ていきましょう。
損失関数は、個々のデータに対するモデルの予測が、実際の値からどれだけ離れているかを測るものです。例えば、ある画像に何が写っているかを予測するモデルを考えてみましょう。一枚の猫の画像を入力した際に、モデルが「犬」と予測したとします。この時の予測の誤差、つまり「猫」と「犬」の差を数値で表したものが損失関数です。画像一枚一枚に対して、このような損失関数の値が計算されます。
一方、目的関数は、訓練データ全体を考慮したモデルの性能を評価します。多くの場合、目的関数は損失関数の平均値を計算することで求められます。つまり、個々のデータに対する損失関数の値をすべて足し合わせ、データの総数で割ることで、モデル全体の平均的な誤差を算出します。この平均値が小さいほど、モデルが訓練データ全体をよく予測できていることを示します。
しかし、目的関数は損失関数の平均値だけではありません。モデルが複雑になりすぎないように調整する仕組みである正則化項が加えられる場合もあります。正則化項を加えることで、学習データには適合できても、未知のデータには対応できない、いわゆる「過学習」を防ぐ効果があります。過学習が起きると、新しいデータに対して精度の高い予測ができなくなってしまうため、正則化項はモデルの汎化性能を高めるために重要な役割を担っています。このように、目的関数は損失関数に加えて、様々な要素を組み込むことができる柔軟な枠組みを提供しています。
| 項目 | 説明 | 例 |
|---|---|---|
| 損失関数 | 個々のデータに対するモデルの予測が、実際の値からどれだけ離れているかを測るもの。 | 猫の画像を入力した際に、モデルが「犬」と予測した時の誤差。 |
| 目的関数 | 訓練データ全体を考慮したモデルの性能を評価する。多くの場合、損失関数の平均値に正則化項を加える。 | 全画像の損失関数の平均値 + 正則化項。 |
| 正則化項 | モデルが複雑になりすぎないように調整する仕組み。過学習を防ぐ効果がある。 | なし |
最適化手法

ある目的を持つ関数の値を最小、あるいは最大にすることを最適化と言います。最適化を実現するためには、様々な計算のやり方が用いられます。これらのやり方を最適化手法と呼びます。最適化は、機械学習をはじめとした様々な分野で重要な役割を担っています。例えば、製品の製造コストを最小にする、商品の売上を最大にするといった問題を解決する際に役立ちます。
代表的な最適化手法の一つに、勾配降下法があります。勾配降下法は、山の斜面を下るように、少しずつ最適な値へと近づいていく方法です。目的関数の値が、山の高さにあたり、その傾きが最も急な方向へとパラメータと呼ばれる値を調整することで、最小値を目指します。この傾きは勾配と呼ばれ、微分を用いて計算します。勾配降下法は、比較的簡単な計算で済むため、広く利用されていますが、初期値の設定によっては、最適ではない局所的な最小値に陥ってしまう可能性があります。
勾配降下法以外にも、様々な最適化手法が存在します。例えば、確率的勾配降下法は、データの一部を用いて勾配を計算することで、計算量を削減し、大規模なデータにも対応できるようにした手法です。また、ニュートン法は、二階微分、つまり勾配の変化率も利用することで、より効率的に最適値を求める手法です。ただし、ニュートン法は、二階微分の計算コストが高いという欠点があります。
このように、それぞれの最適化手法には、得意な点と不得意な点があります。そのため、問題の種類やデータの規模、計算資源などを考慮して、適切な手法を選択することが重要です。最適化手法の選択は、機械学習モデルの学習にかかる時間や、最終的な性能に大きく影響します。適切な手法を選ぶことで、より速く、より良い結果を得ることが可能になります。
| 最適化手法 | 概要 | 利点 | 欠点 |
|---|---|---|---|
| 勾配降下法 | 山の斜面を下るように、少しずつ最適な値へと近づいていく方法。目的関数の傾きが最も急な方向へとパラメータを調整することで、最小値を目指す。 | 比較的簡単な計算で済むため、広く利用されている。 | 初期値の設定によっては、最適ではない局所的な最小値に陥ってしまう可能性がある。 |
| 確率的勾配降下法 | データの一部を用いて勾配を計算することで、計算量を削減し、大規模なデータにも対応できるようにした手法。 | 計算量を削減できる。大規模なデータにも対応可能。 | 勾配の計算が不安定になる場合がある。 |
| ニュートン法 | 二階微分、つまり勾配の変化率も利用することで、より効率的に最適値を求める手法。 | より効率的に最適値を求めることができる。 | 二階微分の計算コストが高い。 |
様々な種類

解きたい問題によって、色々な形の計算式、つまり目的関数を使う必要があります。この目的関数は、機械学習モデルがどのくらい良いかを測るための重要なものです。まるで、料理の味を測るための塩加減計のようなものです。
例えば、写真を見てそれが猫か犬かを当てるような問題、つまり分類問題では、交差エントロピーと呼ばれる計算式がよく使われます。この交差エントロピーは、機械学習モデルが出した答えの確からしさと、本当の答えとのズレ具合を測るものです。モデルの答えが真実に近ければ近いほど、この交差エントロピーの値は小さくなります。料理で言えば、塩加減が丁度良ければ、美味しいと感じるのと同じです。
一方、家の値段を予測するような問題、つまり回帰問題では、平均二乗誤差と呼ばれる計算式がよく使われます。これは、モデルが予測した値と実際の値との差を二乗して、その平均を計算したものです。予測値と実際の値が近ければ近いほど、この平均二乗誤差の値は小さくなります。家の値段をぴったり予測できれば、誤差はゼロになり、平均二乗誤差もゼロになります。
このように、問題の種類に合わせて適切な目的関数を選ぶことが、良い機械学習モデルを作るためには非常に重要です。適切な目的関数を選ぶことで、モデルの性能を最大限に引き出すことができます。これは、料理を作る際に、素材に合った調味料を選ぶのと同じくらい大切です。
さらに、時には、既存の目的関数を組み合わせて新しい目的関数を作る必要も出てきます。これは、新しい料理を作るために、既存の調味料を混ぜ合わせて新しいソースを作るようなものです。様々な目的関数を理解し、使いこなせるようになることで、より複雑な問題にも対応できる、高性能な機械学習モデルを作ることができるようになります。
| 問題の種類 | 目的関数 | 説明 | 例 |
|---|---|---|---|
| 分類問題 | 交差エントロピー | モデルの予測の確からしさと正解とのズレを測定。正解に近いほど値は小さい。 | 画像認識(猫か犬か) |
| 回帰問題 | 平均二乗誤差 | 予測値と実数値の差の二乗の平均。予測が正確に近いほど値は小さい。 | 家の価格予測 |
| その他 | 既存の目的関数の組み合わせ | 複雑な問題に対応するために、複数の目的関数を組み合わせる。 | – |
機械学習における重要性

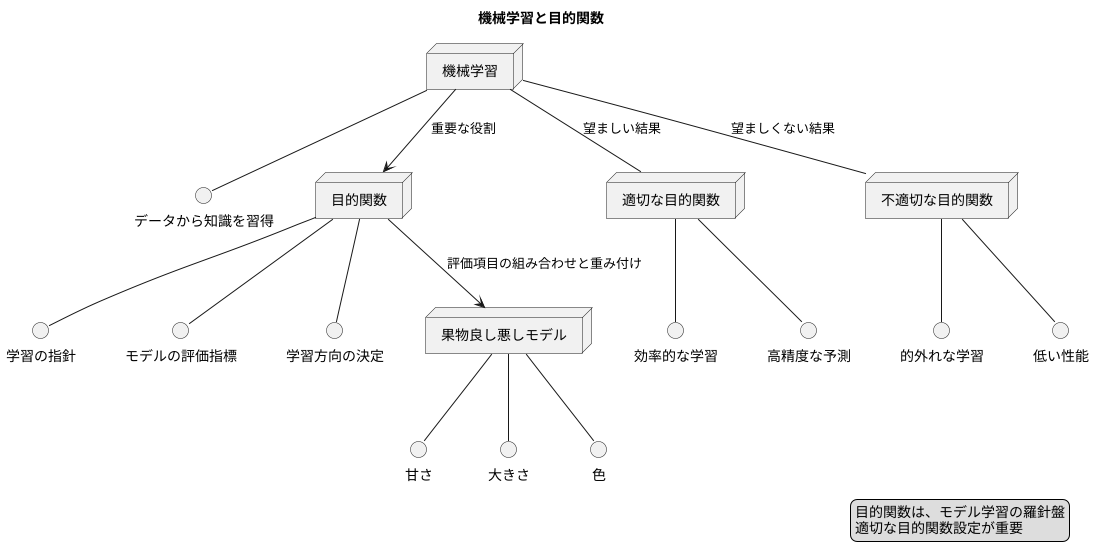
機械学習は、まるで人間の学習と同じように、コンピュータにデータから知識を習得させる技術です。この学習プロセスにおいて、目的関数は非常に重要な役割を担っています。目的関数は、いわば学習の指針となるもので、モデルがどの程度目標に近づいているかを測る物差しと言えます。
例えば、果物の良し悪しを判断するモデルを想像してみてください。甘さ、大きさ、色など、様々な要素を考慮して判断するでしょう。この場合、甘さや大きさ、色などが目的関数における評価項目となります。これらの項目をどのように組み合わせ、どの項目を重視するかは、目的関数によって決定されます。
適切な目的関数を設定することで、モデルはデータから効率的に学習し、精度の高い予測を行うことができます。逆に、目的関数が適切でないと、モデルは的外れな学習をしてしまい、期待した性能を発揮できません。これは、まるで道を指し示す羅針盤が狂っているようなもので、目的地に辿り着くことが難しくなります。
目的関数は、単なる評価指標ではなく、モデルの学習方向を定める羅針盤と言えるでしょう。目的関数の選び方次第で、モデルの性能は大きく変わります。そのため、機械学習に携わる技術者は、目的関数の性質を深く理解し、問題に応じて適切な関数を選択、あるいは新たに設計する能力が求められます。
機械学習技術は日々進歩を続けていますが、目的関数の研究は今後も重要なテーマであり続けるでしょう。より高度な学習を実現するために、新たな目的関数の開発や既存の目的関数の改良が、今後の機械学習の発展に大きく貢献すると考えられます。
今後の展望

機械学習という技術は、まるで生き物のように絶えず進化を続けています。その進化を支える重要な要素の一つに、目的関数があります。目的関数は、機械学習モデルが目指すべき目標を定める羅針盤のような役割を果たしており、この羅針盤の精度が向上することで、より複雑な問題にも対応できるようになります。
現在、様々な分野で目的関数の研究開発が活発に行われています。例えば、複数の目標を同時に達成しようとする多目的最適化の研究は、まるで複数の曲を同時に演奏するオーケストラの指揮者のように、それぞれの目標のバランスを取りながら最適な結果を導き出そうと試みています。また、データの不確実性を考慮したロバスト最適化の研究は、荒波の中でも安定して航行できる船のように、予測不能な状況にも対応できる柔軟なモデルの構築を目指しています。これらの研究は、様々な分野での機械学習の応用可能性を広げ、より高度な問題解決に貢献すると期待されています。
さらに、近年注目を集めている深層学習という技術は、人間の脳のように複雑な構造を持つモデルを扱うため、従来の目的関数では対応が難しいという課題を抱えています。そこで、深層学習モデルの学習に適した新たな目的関数の開発が急務となっています。この新たな羅針盤の開発は、深層学習の更なる発展を促し、より高度な人工知能の実現へと繋がる重要な一歩となるでしょう。
このように、目的関数の研究開発は、機械学習の進化を支える重要な柱であり、今後の更なる発展が期待されています。まるで登山家が山頂を目指すように、研究者たちはより高度な人工知能の実現に向けて、日々挑戦を続けています。その努力は、私たちの未来を大きく変える可能性を秘めていると言えるでしょう。
| 種類 | 説明 | 例え |
|---|---|---|
| 多目的最適化 | 複数の目標を同時に達成する | 複数の曲を同時に演奏するオーケストラの指揮者 |
| ロバスト最適化 | データの不確実性を考慮し、予測不能な状況にも対応できるモデルの構築 | 荒波の中でも安定して航行できる船 |
| 深層学習向け目的関数 | 深層学習モデルの学習に適した新たな目的関数 | (例えなし) |
