正規化:データの範囲を揃える

AIを知りたい
先生、『正規化』ってどういう意味ですか?

AIエンジニア
簡単に言うと、データを一定の範囲、例えば0から1の間に収めるように調整することだよ。例えば、テストの点数を例に考えてみよう。100点満点のテストと50点満点のテストがあったとき、単純に点数だけを比較するのは難しいよね。そこで、正規化を使ってそれぞれの点数を0から1の間に変換すれば、異なる満点のテストでも公平に比較できるようになるんだ。

AIを知りたい
なるほど。でも、なぜ0から1の間なんですか?他の範囲ではダメなんですか?

AIエンジニア
0から1の間にするのは、データのばらつきを分かりやすくするためだよ。この範囲を使うことで、異なる種類のデータでも比較しやすくなるんだ。もちろん、他の範囲を使うこともできるけど、0から1の間が一般的だね。ただし、極端に大きな値や小さな値(外れ値)があると、うまく調整できないこともあるから注意が必要だよ。
正規化とは。
AIでよく使われる言葉に「正規化」というものがあります。これは、データを一定の範囲に調整する方法の一つです。この方法は、データの中で一番大きい値と一番小さい値がわかっている時に役立ちます。具体的には、データ全体を0から1の範囲に変換します。ただし、正規化は極端に大きい値や小さい値に影響されやすいという弱点があります。もし、そのような極端な値がある場合は、「標準化」という別の方法を使った方が良い結果が得られます。
正規化とは

情報をうまく扱うために、数値を一定の範囲に整える作業を「正規化」と言います。多くの場合、0から1の範囲に調整します。この作業は、異なる種類や大きさの数値をまとめて扱う際にとても役立ちます。
たとえば、人の身長、体重、年齢を考えてみましょう。これらの数値は、それぞれ単位も違えば、数値の大きさも全く違います。もし、これらの数値をそのまま使って計算などを行うと、身長や体重といった大きな数値が、年齢といった小さな数値よりも結果に大きな影響を与えてしまう可能性があります。これは、ちょうど、大きな声の人と小さな声の人が一緒に話すと、大きな声の人にばかり気を取られてしまうようなものです。
正規化を行うことで、身長、体重、年齢といった異なる種類の数値を、同じくらいの大きさの範囲に変換することができます。たとえば、一番高い人と一番低い人の身長を0と1に対応させ、その間の身長の人は0と1の間の数値に対応させます。体重や年齢についても同様に0から1の範囲に変換します。こうすることで、どの数値も同じくらいの影響力を持つようになり、バランスの取れた計算や分析を行うことができます。
正規化は、数値の最大値と最小値がわかっている場合に特に効果的です。最大値と最小値を使うことで、すべての数値を0から1の範囲にきちんと収めることができます。この方法は、機械学習といった複雑な計算処理を行う際によく用いられます。機械学習では、大量のデータを使ってコンピュータに学習させるため、データのバランスを整える正規化が重要な役割を果たします。
このように、正規化は数値データを扱う上で欠かせない作業の一つであり、様々な分野で広く活用されています。
| 正規化 | 数値を一定範囲(例:0〜1)に整える作業 |
|---|---|
| メリット | 異なる種類や大きさの数値をまとめて扱える 例:身長、体重、年齢のように単位や桁が違うデータを比較可能にする |
| 例 | 身長の正規化: 最大身長 → 1 最小身長 → 0 その他 → 0〜1の間の数値 |
| 効果的な場面 | 最大値と最小値が既知の場合 機械学習などの複雑な計算処理 |
| 役割 | データのバランス調整 数値データ処理における重要な作業 |
正規化の計算方法

データの正規化は、異なる範囲の値を持つ複数のデータを比較したり、機械学習モデルの学習をスムーズに進めるために欠かせない手法です。正規化を行うことで、すべてのデータが0から1の範囲に統一されます。この範囲への変換は、単純な計算式に従って行われます。正規化の計算は、まず正規化したいデータの全体を見て、その中の最大値と最小値を見つけ出すことから始まります。次に、個々のデータから最小値を引きます。これは、すべてのデータを同じ出発点に揃えるための操作です。そして、この結果を最大値と最小値の差で割ります。この差は、元のデータの広がり具合を表しています。この計算手順を数式で表現すると、正規化後の値 x’ は、元の値 x、最小値 min(x)、最大値 max(x) を用いて、x’ = (x – min(x)) / (max(x) – min(x)) となります。
具体的な例を挙げて考えてみましょう。例えば、{2, 4, 6, 8} というデータがあったとします。このデータの中で一番小さい値は2、一番大きい値は8です。値4を正規化してみましょう。まず、4から最小値の2を引きます。結果は2です。次に、この2を最大値8と最小値2の差、つまり6で割ります。すると、2 / 6 = 0.333… となり、値4の正規化後の値は0.333… となります。同様に、値2、6、8を正規化すると、それぞれ (2 – 2) / (8 – 2) = 0、(6 – 2) / (8 – 2) = 0.666…、(8 – 2) / (8 – 2) = 1 となります。このように、正規化は簡単な計算でデータの範囲を0から1に変換することができ、データの比較や解析を容易にします。 また、この手法は最小最大正規化とも呼ばれ、データの範囲が事前に分かっている場合に有効です。しかし、外れ値の影響を受けやすいという欠点も持っています。そのため、データの特性を理解した上で、適切な正規化手法を選ぶことが重要です。
正規化と標準化の違い

数値データを扱う場面では、データの範囲や分布が結果に大きく影響することがあります。そのため、データの尺度を調整する処理は重要です。よく使われる手法として、正規化と標準化があります。どちらもデータの尺度を整えますが、その方法は異なります。
正規化は、データの値を特定の範囲、例えば0から1の間に変換する手法です。元のデータの最小値が0、最大値が1になり、他の値はその間に収まります。この手法は、データの範囲を固定するため、異なる尺度を持つ複数のデータを比較しやすくなるという利点があります。例えば、テストの点数と身長のように、単位や範囲の異なるデータを扱う場合に有効です。しかし、極端に大きな値や小さな値(外れ値)の影響を受けやすいという欠点も持ちます。もしデータの中に突出した値があると、他のデータの値が圧縮されてしまい、データの本来の特徴が失われる可能性があります。
一方、標準化は、データの平均値を0、標準偏差を1に変換する手法です。これは、それぞれのデータが平均値からどれくらい離れているかを標準偏差を基準に表すことを意味します。標準化は、外れ値の影響を受けにくいという利点があります。なぜなら、平均値や標準偏差は外れ値の影響をある程度吸収するため、極端な値に引っ張られることが少ないからです。しかし、標準化されたデータは特定の範囲に収まるとは限りません。そのため、データの範囲が重要な役割を果たすアルゴリズムには適さない場合があります。また、データが正規分布に近い場合に有効な手法であり、そうでない場合は効果が薄れる可能性があります。
正規化と標準化、どちらの手法を選択するかは、データの特性や使用するアルゴリズムによって慎重に検討する必要があります。データに外れ値が含まれていて、その影響を抑えたい場合は標準化が適しています。一方、データの範囲を固定し、異なる尺度のデータを比較したい場合は正規化が適しています。それぞれの長所と短所を理解し、適切な手法を選ぶことが重要です。
| 手法 | 説明 | 長所 | 短所 | 適したケース |
|---|---|---|---|---|
| 正規化 | データを特定の範囲(例:0〜1)に変換 | 異なる尺度のデータの比較が容易 | 外れ値の影響を受けやすい | データの範囲を固定し、異なる尺度のデータを比較したい場合 |
| 標準化 | データの平均値を0、標準偏差を1に変換 | 外れ値の影響を受けにくい | 特定の範囲に収まらない、データが正規分布に近い場合に有効 | データに外れ値が含まれていて、その影響を抑えたい場合 |
正規化の応用例

数値を一定の範囲に揃える整え方のことを、正規化と言います。この整え方は、様々な分野で広く役立てられています。例えば、写真や絵などの画像を取り扱う画像処理では、色の濃さを表す数値を0から1の範囲に揃えることで、写真の明るさや色の鮮やかさを調整することができます。
機械学習の分野でも、正規化は重要な役割を担っています。機械学習では、様々な種類のデータを数値に変換して処理を行います。しかし、データの種類によって数値の範囲が大きく異なる場合、学習の効率が悪くなってしまうことがあります。例えば、画像認識の場合、画像の色の濃さは通常0から255までの数値で表されますが、このデータをそのまま学習に使うと、色の濃さの範囲が学習に悪い影響を与える可能性があります。そこで、色の濃さを表す数値を0から1の範囲に正規化することで、学習を安定させ、より良い結果を得ることができるようになります。
また、文章を扱う自然言語処理の分野でも、正規化は欠かせない技術です。例えば、ある単語が文章中に何回出てきたかを数える場合、そのままの回数を使うのではなく、文章全体の長さで割って、文章の長さの影響を取り除いた数値を使うことがよくあります。こうすることで、異なる長さの文章でも単語の出現頻度を適切に比較することができます。他にも、単語の意味を数値で表すときにも、正規化が用いられます。単語の意味を表す数値の範囲を一定の範囲に揃えることで、計算を安定させたり、異なる単語の意味を比較しやすくしたりすることができます。このように、正規化は様々な場面でデータを扱いやすくするために役立っているのです。
| 分野 | 正規化の例 | 効果 |
|---|---|---|
| 画像処理 | 色の濃さを0から1の範囲に揃える | 写真の明るさや色の鮮やかさを調整 |
| 機械学習 | 色の濃さを0から1の範囲に正規化 | 学習の安定化、より良い結果 |
| 自然言語処理 | 単語の出現回数を文章全体の長さで割る | 異なる長さの文章でも単語の出現頻度を適切に比較 |
| 自然言語処理 | 単語の意味を表す数値の範囲を一定の範囲に揃える | 計算の安定化、異なる単語の意味の比較 |
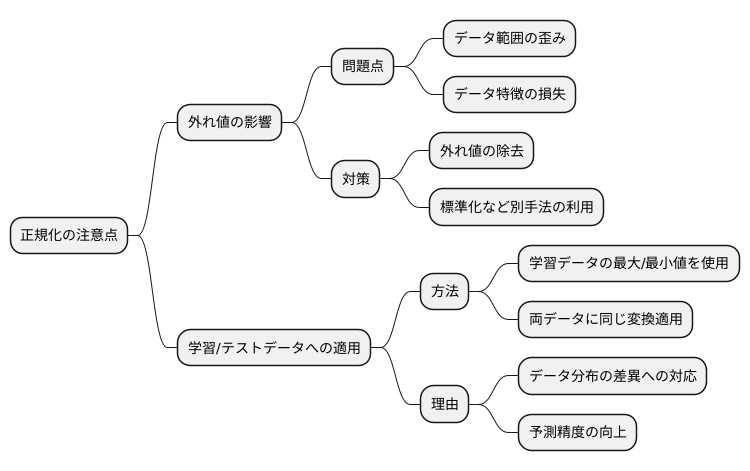
正規化の注意点

数値を一定の範囲に揃える操作、正規化を行う際には、いくつか注意すべき点があります。その中でも特に重要なのは、大きく外れた値、いわゆる外れ値が与える影響についてです。正規化は、データの最大値と最小値を使って計算を行います。そのため、もし外れ値がデータの中に紛れ込んでいると、本来のデータの範囲が大きく歪んでしまうことがあります。
例を挙げて考えてみましょう。ほとんどのデータが0から100の間に収まっているとします。そこに、1000という極端に大きな値が一つだけ混ざっていたとしましょう。このデータセットを正規化すると、0から100までの値は、非常に小さな値に変換されてしまいます。結果として、データ全体の分布が大きく変わってしまい、本来のデータの特徴が失われてしまうのです。
このような外れ値の影響を防ぐためには、二つの方法があります。一つは、外れ値をあらかじめ取り除いておくことです。もう一つは、標準化など、外れ値の影響を受けにくい別の方法を使うことです。
もう一つ、正規化を行う上で重要な点は、学習用データとテスト用データへの適用方法です。それぞれのデータに個別に正規化を適用するのではなく、学習用データから得られた最大値と最小値を用いて、学習用データとテスト用データの両方を正規化する必要があります。なぜなら、学習用データとテスト用データでデータの分布が異なる場合、個別に正規化してしまうと、学習時に得られた知識がテストデータにうまく適用できず、結果として予測精度が下がってしまう可能性があるからです。
つまり、正規化を正しく行うためには、外れ値への適切な対処と、学習用データとテスト用データへの一貫した適用が不可欠と言えるでしょう。