平均二乗対数誤差:機械学習での活用

AIを知りたい
先生、「平均二乗対数誤差」って、何ですか?よくわからないです。

AIエンジニア
簡単に言うと、予測値と正解値のずれを、対数を使って見ている誤差のことだよ。たとえば、正解が10で予測が1の時と、正解が100で予測が10の時は、どちらも10倍ずれているよね。普通の誤差だと1と90で大きく違うけど、対数を使うとこのずれ具合を同じように評価できるんだ。

AIを知りたい
なるほど。でも、なぜ対数を使うんですか?

AIエンジニア
それはね、正解値と予測値の比率が重要な場合に有効なんだ。例えば、株価の予測とか、売上予測とか。小さな値の時のずれよりも、大きな値の時のずれを小さく評価したい時に使うんだよ。あと、計算上都合が良い場合もあるね。
平均二乗対数誤差とは。
人工知能の分野でよく使われる言葉に「平均二乗対数誤差」というものがあります。これは、機械学習の分野で使われる計算方法の一つです。この計算では、本来の値と予想した値の差を対数を使って表し、その差を二乗して平均することで、予想の正確さを測ります。対数を用いる計算では、本来の値と予想した値、どちらを先に置くかは問題ではありません。
対数誤差とは

対数誤差は、予測した値と本当の値との差を測る方法のひとつですが、普通の方法とは少し違います。通常、誤差を計算する時は、予測値と本当の値をそのまま引き算します。しかし、対数誤差では、それぞれの値の対数を計算してから引き算を行います。これは、両者の比率に注目した誤差の測り方と言えます。
例えば、本当の値が10で予測値が1の場合を考えてみましょう。この時、両者の差は9です。次に、本当の値が1000で予測値が100の場合を考えます。この場合も差は9です。どちらも差は同じですが、よく見ると、最初の例では予測値は本当の値の10分の1、次の例でも予測値は本当の値の10分の1になっています。つまり、差は同じでも比率は同じなのです。対数誤差を使うと、このような比率の違いをうまく捉えることができます。
対数を使うと、大きな値の影響が小さくなり、小さな値の影響が大きくなります。例えば、100と101の差は1ですが、対数を取ると差は約0.0043になります。一方で、1と2の差は1ですが、対数を取ると差は約0.69になります。このように、対数は値の変化の割合を重視するため、本当の値が大きく変動するデータの場合に特に役立ちます。
対数誤差の計算式は、一般的に「予測値の対数−本当の値の対数」を使います。しかし、「本当の値の対数−予測値の対数」を使っても構いません。大切なのは、どちらの計算式を使うかを統一することです。そうすることで、誤差の意味を正しく理解し、比較することができます。
| 項目 | 説明 | 例 |
|---|---|---|
| 対数誤差 | 予測値と真値の比率に着目した誤差。それぞれの値の対数を計算してから引き算を行う。 | 真値10, 予測値1 -> 差9 (比率1/10) 真値1000, 予測値100 -> 差9 (比率1/10) |
| 対数の効果 | 大きな値の影響を小さく、小さな値の影響を大きくする。値の変化の割合を重視。 | 100と101の差1 -> 対数差 約0.0043 1と2の差1 -> 対数差 約0.69 |
| 計算式 | 一般的に「予測値の対数−本当の値の対数」だが、「本当の値の対数−予測値の対数」も可。重要なのは統一すること。 | – |
平均二乗対数誤差の定義

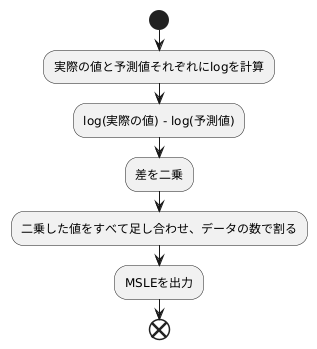
平均二乗対数誤差(略してエムエスエルイー)は、予測の良し悪しを測るものさしの一つです。専門的には、損失関数と呼ばれるものの一つです。これは、機械学習などで、モデルがどれくらい正確に予測できているかを評価するために使われます。
エムエスエルイーを計算するには、まず実際の値と予測値のそれぞれに、対数の計算をします。対数を使うことで、実際の値と予測値の比率に着目することができます。例えば、実際の値が10で予測値が1の場合と、実際の値が100で予測値が10の場合、どちらも10倍のずれがありますよね。このような場合、対数を使うことで、ずれの大きさを同じように扱うことができます。
次に、対数を計算した後の実際の値と予測値の差を求め、それを二乗します。二乗する理由は二つあります。一つは、差が正の数か負の数かを気にせずに、ずれの大きさだけを考えられるようにするためです。もう一つは、大きなずれをより強調するためです。
最後に、二乗した値をすべて足し合わせ、データの数で割って平均値を求めます。これがエムエスエルイーの値です。エムエスエルイーの値が小さいほど、予測が正確であると言えます。
エムエスエルイーは、特に実際の値が大きく変わる場合に有効です。例えば、商品の売り上げや株価などは、日によって大きく変動することがあります。このような場合、エムエスエルイーを使うことで、予測の精度を適切に評価することができます。
まとめると、エムエスエルイーは、対数を使って比率のずれを測り、二乗してずれの大きさと大きなずれの影響を強調し、平均することで全体的なずれの大きさを示すものさしです。特に、値が大きく変動するデータに適しています。
平均二乗誤差との違い

平均二乗誤差(エムエスイー)と平均二乗対数誤差(エムエスエルイー)は、どちらも機械学習モデルの予測精度を評価する指標ですが、誤差の捉え方が異なります。その違いは、誤差を計算する際に用いる値にあります。エムエスイーは、実際の値と予測値の単純な差を二乗し、その平均を計算します。一方、エムエスエルイーは、実際の値と予測値のそれぞれを対数変換した後の差を二乗し、その平均を計算します。
この違いにより、エムエスイーとエムエスエルイーは異なる性質を持ちます。エムエスイーは、誤差の大きさそのものを重視します。実際の値と予測値の差が大きいほど、エムエスイーの値も大きくなります。例えば、実際の値が10で予測値が1の場合と、実際の値が1000で予測値が991の場合、エムエスイーはどちらも81となります。つまり、エムエスイーは誤差の絶対量に注目していると言えます。
一方、エムエスエルイーは誤差の比率を重視します。実際の値に対する予測値の比率が大きく異なる場合、エムエスエルイーの値は大きくなります。前述の例で言えば、実際の値が10で予測値が1の場合は、実際の値が1000で予測値が991の場合よりもエムエスエルイーの値は大きくなります。これは、前者の比率(1/10)が後者の比率(991/1000)よりも小さいためです。つまり、エムエスエルイーは予測値が実際の値の何倍あるいは何分の一かという点に注目していると言えます。
このように、エムエスイーとエムエスエルイーはそれぞれ異なる視点で誤差を評価します。そのため、どちらの指標を用いるかは、評価したい内容に合わせて適切に選択する必要があります。例えば、絶対的な誤差の大きさが重要な場合はエムエスイーを、相対的な誤差の大きさが重要な場合はエムエスエルイーを用いると良いでしょう。
| 指標 | 計算方法 | 重視する点 | 性質 | 使用例 |
|---|---|---|---|---|
| 平均二乗誤差 (MSE) | (実際の値 – 予測値)^2 の平均 | 誤差の大きさ | 誤差の絶対量に注目 | 絶対的な誤差の大きさが重要な場合 |
| 平均二乗対数誤差 (MSLE) | (log(実際の値) – log(予測値))^2 の平均 | 誤差の比率 | 予測値が実際の値の何倍あるいは何分の一かという点に注目 | 相対的な誤差の大きさが重要な場合 |
平均二乗対数誤差の利点

平均二乗対数誤差(略して平均二乗対数誤差)には、予測の良し悪しを測る方法として、いくつかの長所があります。特に、実測値と予測値の比率に着目することで、数値の大小にかかわらず、誤差を適切に評価できます。
これは、例えば商品の売上予想のように、実際の値が大きく変動するデータで特に有効です。売上が少ない商品の予測が大きく外れると、全体の売上予測にも無視できない影響が出ます。しかし、通常の誤差計算方法では、売上の多い商品の誤差に比べて、売上が少ない商品の誤差は小さく見えてしまうことがあります。平均二乗対数誤差を使うことで、売上が少ない商品の予測精度を高めることに重点を置くことができ、結果として全体の売上予測の精度向上に繋がります。
もう一つの利点は、突出した値、いわゆる外れ値の影響を受けにくいことです。外れ値は、他のデータから大きく外れた値で、予測のモデルを作る際に悪影響を及ぼす可能性があります。例えば、ある商品の売上が、特別なキャンペーンの影響で一時的に急増した場合、その値を外れ値として捉えることができます。平均二乗対数誤差は、対数を使うことで、これらの外れ値の影響を和らげ、より安定した予測モデルを作ることができます。つまり、一時的な売上急増に惑わされず、通常の売上傾向を捉えた予測が可能になります。
このように、平均二乗対数誤差は、データのばらつきが大きい場合や外れ値が含まれる場合に特に有効な指標と言えるでしょう。
| 平均二乗対数誤差の利点 | 説明 |
|---|---|
| 数値の大小に関わらず適切な評価 | 実測値と予測値の比率に着目するため、売上の大小にかかわらず誤差を適切に評価。売上予測のような変動の大きいデータで有効。 |
| 売上予測全体精度の向上 | 売上が少ない商品の予測精度向上に重点を置くことができ、結果として全体の売上予測精度向上に貢献。 |
| 外れ値の影響を受けにくい | 対数を使用することで外れ値の影響を軽減。一時的な売上急増に惑わされず、通常の売上傾向を捉えた予測が可能。 |
平均二乗対数誤差の欠点

平均二乗対数誤差(略して平均二乗対数誤差と呼ぶこともあります)は、機械学習などで予測の良し悪しを測る指標の一つですが、いくつかの弱点があります。まず、この指標は予測値の対数を用いて計算するため、予測値がゼロやマイナスの値の場合には計算できません。ゼロやマイナスが出てくるかもしれない予測に使うことは避けるべきです。
次に、平均二乗対数誤差は比率の違いに敏感で、実際の値の差はあまり考慮しません。例えば、本当の値が100で予測が90の場合と、本当の値が10で予測が9の場合を比べてみましょう。どちらも10の差ですが、前者は10%のずれ、後者は10%のずれです。平均二乗対数誤差では、比率のずれが同じなので、どちらの場合も同じ値になります。しかし、実際の差は10と90で大きく違います。もし、値の差を重視したい場合は、平均二乗誤差など、他の指標を使うべきです。
最後に、平均二乗対数誤差は、その値の意味を理解するのが難しいという問題点もあります。平均二乗誤差は、誤差を二乗したものの平均なので、元のデータの単位の二乗が指標の単位になります。しかし、平均二乗対数誤差は対数を二乗したものの平均なので、単位がはっきりしません。そのため、結果をどう読み解くかには注意が必要です。これらの欠点を理解した上で、適切な場面で使うことが重要です。
| 弱点 | 説明 | 例 | 対策 |
|---|---|---|---|
| ゼロ以下の値を予測できない | 予測値がゼロやマイナスの値の場合には計算できない | N/A | ゼロやマイナスが出てくるかもしれない予測に使うことは避ける |
| 比率の違いに敏感、実際の値の差を考慮しない | 実際の値の差よりも比率の差を重視する | 真値100, 予測90(差10)と真値10, 予測9(差1)は同じ比率のずれとして評価される | 値の差を重視したい場合は、平均二乗誤差など、他の指標を使う |
| 値の意味を理解しにくい | 対数を二乗したものの平均なので、単位がはっきりしない | N/A | 結果の解釈に注意する |
平均二乗対数誤差の適用事例

平均二乗対数誤差(へいきんにじょうたいすうごさ)は、様々な分野で活用されています。その中でも、特に需要予測は、この手法が力を発揮する代表的な例です。商品の需要は、季節、流行、景気など様々な要因によって大きく変動します。そのため、予測が難しいとされていますが、平均二乗対数誤差を用いることで、より正確な予測値を導き出すことが可能になります。なぜなら、この手法は、予測値と実際の値の比率に着目するため、需要の変動幅が大きい場合でも、安定した予測結果を得ることができるからです。
売上予測も、平均二乗対数誤差が有効に活用される分野の一つです。売上高は、需要と同様に、様々な要因に影響を受け、予測が難しい指標です。しかし、平均二乗対数誤差を用いることで、需要予測と同様に、より正確な売上予測が可能になります。特に、新商品の発売時やキャンペーン実施時など、売上の変動が大きい時期においても、この手法は、安定した予測結果を提供します。
金融分野においても、平均二乗対数誤差は重要な役割を果たしています。株価は、市場の動向や企業の業績など、様々な要因によって大きく変動します。そのため、株価予測は非常に難しいとされていますが、平均二乗対数誤差を用いることで、株価の変動率を予測することが可能になります。これにより、投資家は、より的確な投資判断を行うことができます。
インターネットの世界でも、平均二乗対数誤差は活用されています。ウェブサイトへのアクセス数は、時間帯や曜日、季節、イベントなど、様々な要因によって大きく変動します。そのため、アクセス数の予測は難しいとされていますが、平均二乗対数誤差を用いることで、より正確なアクセス数予測が可能になります。これにより、ウェブサイト運営者は、サーバーの負荷を予測し、適切な対策を講じることが可能になります。このように、平均二乗対数誤差は、様々な分野で予測精度を高めるために活用され、その効果を発揮しています。
| 分野 | 説明 |
|---|---|
| 需要予測 | 季節、流行、景気など様々な要因によって変動する需要を、比率に着目することでより正確に予測。 |
| 売上予測 | 需要と同様に様々な要因に影響される売上高を、より正確に予測。特に新商品発売時やキャンペーン実施時など、変動が大きい時期に有効。 |
| 金融 | 市場の動向や企業の業績など、様々な要因によって変動する株価の変動率を予測し、投資判断を支援。 |
| インターネット | 時間帯、曜日、季節、イベントなど様々な要因によって変動するウェブサイトへのアクセス数を予測し、サーバー負荷対策に役立てる。 |
