平均二乗誤差:機械学習の基本概念

AIを知りたい
先生、「平均二乗誤差」ってよく聞くんですけど、どんなものか教えてください。

AIエンジニア
簡単に言うと、予想した値と本当の値との違いを二乗して、その平均を取ったものだよ。例えば、気温を予想して、実際の気温との違いを測る時に使えるんだ。

AIを知りたい
二乗するっていうのは、なぜですか?

AIエンジニア
違いが大きいものほど、より大きな値になるようにするためだよ。そうすることで、大きく外れた予想をより重視することができるんだ。ただ、その反面、極端に外れた値に影響されやすいという欠点もあるけどね。
平均二乗誤差とは。
人工知能の分野でよく使われる言葉に「平均二乗誤差」というものがあります。これは、予測した値と実際の値がどれくらい離れているかを測る尺度の一つで、特に数値を予測する問題で使われます。具体的には、それぞれの予測値と正解値の差を二乗して、その平均を計算します。この値が小さいほど、予測が正確だったことを意味します。二乗することによって、大きなずれはより大きな値として扱われるため、外れた値の影響を強く受けるという特徴があります。予測の良し悪しを評価する際には、この性質が役に立つこともありますが、学習の過程で使う場合には、極端に外れた値に引っ張られてしまうという欠点にもなり得ます。
はじめに

機械学習という、まるで機械が自ら学ぶかのような技術の分野では、作り上げた予測模型の良し悪しを測る物差しがいくつも存在します。様々な予測問題の中でも、気温や株価といった連続した数値を予測する、いわゆる回帰問題において、最も基本的な指標の一つが平均二乗誤差です。この平均二乗誤差は、予測値と実際の値のずれ具合を示す物差しで、モデルの精度を評価する上で欠かせない役割を担っています。
平均二乗誤差は、個々のデータ点における予測値と実測値の差を二乗し、それらを全て足し合わせ、データ数で割ることで計算します。二乗する理由は、ずれの大きさを強調するためです。例えば、予測値と実測値の差が正負で相殺されてしまうのを防ぎ、全体のずれ具合を正しく反映させることができます。この計算方法は一見複雑に思えるかもしれませんが、実際の計算は単純な四則演算の繰り返しです。
平均二乗誤差は、値が小さいほど予測精度が高いことを示します。値がゼロであれば、予測値と実測値が完全に一致している、つまり完璧な予測を意味します。しかし、現実世界のデータにはノイズが含まれることが多く、完璧な予測はほぼ不可能です。そのため、平均二乗誤差を最小にすることを目指し、モデルの改良を繰り返します。
平均二乗誤差には利点だけでなく欠点も存在します。大きなずれを持つ外れ値の影響を受けやすいという点が代表的な欠点です。少数の外れ値によって平均二乗誤差が大きく変動してしまうため、外れ値への対策が必要となる場合もあります。外れ値への対策としては、ロバストな回帰手法を用いたり、前処理で外れ値を除去するといった方法が考えられます。このように、平均二乗誤差は単純で理解しやすい一方で、扱うデータの特徴を考慮する必要がある指標と言えるでしょう。
| 指標名 | 説明 | 計算方法 | 評価 | 利点 | 欠点 | 対策 |
|---|---|---|---|---|---|---|
| 平均二乗誤差 | 連続値予測(回帰問題)における予測精度を示す基本指標。予測値と実測値のずれ具合を測る。 | 個々のデータ点の予測値と実測値の差を二乗し、合計後、データ数で割る。 | 値が小さいほど予測精度が高い。0は完璧な予測。 | 計算が単純。理解しやすい。 | 外れ値の影響を受けやすい。 | ロバストな回帰手法、外れ値の前処理による除去 |
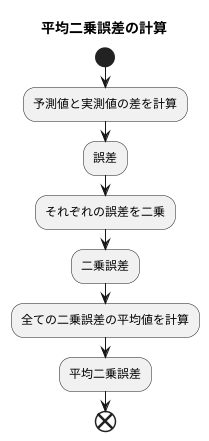
計算方法

計算方法を具体的に説明します。 平均二乗誤差は、機械学習モデルの予測精度を評価する指標の一つであり、モデルの予測値と実際の値がどれだけ離れているかを測る尺度です。この値が小さいほど、モデルの予測精度が高いと言えます。
まず、予測値と実測値の差を計算します。この差を「誤差」と呼びます。例えば、ある商品の売上げを予測するモデルがあり、今日の売上げを100個と予測し、実際の売上げが120個だったとします。この場合、誤差は120から100を引いた20となります。もし予測が80個だったら、誤差は120から80を引いた40となります。
次に、それぞれの誤差を二乗します。これは、誤差に正負の値がある場合に、それらを全て正の値に変換し、大きな誤差の影響をより強く反映させるためです。先ほどの例で、誤差が20の場合は二乗して400、誤差が40の場合は二乗して1600となります。このように二乗することで、40の誤差は20の誤差に比べて4倍の影響力を持つことになります。
最後に、全ての二乗した誤差の平均値を計算します。これが平均二乗誤差です。例えば、10日間の売上げデータを予測し、それぞれの誤差を二乗した値が100、400、900、…、10000だったとします。これらの合計を10で割ると平均二乗誤差が得られます。 このようにして計算された平均二乗誤差は、モデルの予測精度を評価する上で重要な指標となります。
より小さな平均二乗誤差を目指すことで、より精度の高い予測モデルを構築することができます。
利点

平均二乗誤差には、幾つかの利点があります。まず第一に、計算が容易という点が挙げられます。複雑な計算式などを用いることなく、単純な足し算、掛け算、割り算といった算術演算だけで計算できます。そのため、計算方法を理解しやすく、プログラムなどへの実装も容易に行えます。また、計算にかかる時間も短く、コンピュータへの負担も少ないため、大規模なデータセットに対しても効率的に計算できます。
第二に、大きな誤差をより強調するという効果があります。誤差を二乗することで、小さな誤差は比較的小さな値のままですが、大きな誤差は非常に大きな値になります。例えば、誤差が2倍になると、二乗した値は4倍になり、誤差が3倍になると二乗した値は9倍になります。これは、データの中に他のデータから大きく外れた値、いわゆる外れ値が混ざっている場合に特に有効です。平均二乗誤差を用いることで、これらの外れ値の影響を大きく反映させることができ、モデルが外れ値に過剰に適合することを防ぐことができます。
第三に、数学的に扱いやすいという利点があります。平均二乗誤差は微分可能な関数であるため、最適化アルゴリズムを用いてモデルのパラメータを調整する際に、勾配と呼ばれる変化の割合を容易に計算できます。この勾配を用いることで、モデルの予測精度を効率的に向上させることができます。他の指標の中には、微分ができない、もしくは計算が複雑なものも存在しますが、平均二乗誤差は数学的に扱いやすい指標であるため、様々な場面で利用されています。
このように、平均二乗誤差は計算の容易さ、大きな誤差の強調、数学的な扱いやすさといった利点を持つため、様々な分野で広く利用されている指標と言えるでしょう。
| 利点 | 説明 |
|---|---|
| 計算が容易 | 単純な算術演算のみで計算可能。理解しやすく、実装も容易。計算時間も短く、大規模データにも効率的。 |
| 大きな誤差を強調 | 誤差を二乗することで、大きな誤差の影響を大きく反映。外れ値の影響を捉え、過剰適合を防止。 |
| 数学的に扱いやすい | 微分可能な関数のため、勾配の計算が容易。最適化アルゴリズムを用いてモデルの精度向上に効果的。 |
欠点

平均二乗誤差は、モデルの予測値と実際の値との差を二乗して平均したもので、モデルの性能を測る指標として広く使われています。しかし、この指標にはいくつか弱点があります。最も大きな弱点は、まれにしか現れない大きく外れた値、いわゆる外れ値に大きく左右されてしまうことです。
平均二乗誤差は誤差を二乗するため、たった一つの外れ値でも全体の値を大きく押し上げてしまう可能性があります。例えば、ほとんどのデータで予測と実際の値が近いにも関わらず、一つだけ大きく外れたデータがあると、二乗した誤差が非常に大きくなり、平均二乗誤差も大きくなってしまうのです。これは、モデルの真の性能を正しく反映していない可能性があります。
ほとんどの場合で高い予測精度を示しているモデルでも、少数の外れ値によって平均二乗誤差が大きくなってしまい、誤って性能が低いと判断されるかもしれません。例えば、ある商品の来月の売上予測モデルを考えてみましょう。ほとんどの商品の売上予測は正確だったとしても、新商品の発売など、予測が難しい特別な事情により、ある商品の売上予測が大きく外れてしまうかもしれません。この場合、平均二乗誤差は大きくなり、モデル全体の性能が低いと評価されてしまう可能性があります。しかし、新商品発売のような特別なケースを除けば、モデルは高い精度で予測を行えているはずです。
このように、外れ値の影響を受けやすいという平均二乗誤差の弱点を踏まえると、特に外れ値が多いデータの場合には、平均二乗誤差だけでなく、中央値絶対偏差や分位点平均など、外れ値の影響を受けにくい他の指標も併せて使うことが大切です。複数の指標を組み合わせて使うことで、モデルの性能をより多角的に評価し、誤った判断を防ぐことができます。
| 指標 | 説明 | 弱点 | 対応策 |
|---|---|---|---|
| 平均二乗誤差 | モデルの予測値と実際の値との差を二乗して平均したもの | 外れ値に大きく左右される | 中央値絶対偏差や分位点平均など、外れ値の影響を受けにくい他の指標も併せて使う |
他の指標との比較

予測の正確さを測る方法は、平均二乗誤差以外にもたくさんあります。それぞれの方法には得意不得意があり、状況に応じて使い分けることが大切です。どの方法を選ぶかは、扱うデータの性質や、最終的に何を達成したいかによって変わってきます。
例えば、平均絶対誤差という方法を見てみましょう。これは、実際の値と予測値の差の絶対値を平均したものです。平均二乗誤差と比べると、突出して大きなずれ(外れ値)の影響を受けにくいという特徴があります。もし外れ値が多いデータで平均二乗誤差を使うと、その外れ値に引っ張られて、モデルの本当の良し悪しが見えにくくなってしまうことがあります。そんな時は、平均絶対誤差の方が適していると言えるでしょう。
また、決定係数という指標もあります。これは、モデルがデータのばらつきをどれくらい説明できているかを表すものです。1に近いほど、モデルがデータをよく説明できていると解釈します。もし、データ全体のばらつきが大きく、そのばらつきをモデルがうまく捉えているなら、決定係数は高い値を示します。逆に、データのばらつきが小さく、モデルがそのばらつきを説明できていなければ、決定係数は低い値になります。
このように、様々な指標を組み合わせて見ることで、モデルの性能を多角的に評価することができます。それぞれの指標が何を意味していて、どんな時に使うべきかを理解することが、より良い予測モデルを作るための鍵となります。目的に合わせて最適な指標を選び、データの特性を考慮しながら分析を進めることが重要です。
| 指標名 | 説明 | 長所 | 短所 | 適した状況 |
|---|---|---|---|---|
| 平均絶対誤差 | 実際の値と予測値の差の絶対値を平均したもの | 外れ値の影響を受けにくい | – | 外れ値が多いデータ |
| 平均二乗誤差 | 実際の値と予測値の差の二乗を平均したもの | – | 外れ値の影響を受けやすい | 外れ値が少ないデータ |
| 決定係数 | モデルがデータのばらつきをどれくらい説明できているかを表すもの | モデルの説明力を示す | – | データ全体のばらつきとモデルの説明力の関係性を評価したい場合 |
まとめ

この記事では、機械学習の分野でよく使われる予測の正確さを測る方法の一つ、平均二乗誤差について詳しく説明しました。
平均二乗誤差とは、簡単に言うと、実際の値と予測値の差を二乗して平均したものです。この値が小さいほど、予測が正確であることを示します。計算方法は単純で、それぞれのデータについて実際の値と予測値の差を二乗し、それらを全て足し合わせてデータの数で割るだけです。
平均二乗誤差を使うメリットは、計算が容易であるという点です。複雑な計算を必要としないため、手軽に利用できます。また、誤差を二乗することで、大きな誤差をより強調することができます。これは、大きなずれをより深刻な問題として捉え、モデルの改善に役立てる上で重要です。
一方で、平均二乗誤差にはデメリットもあります。極端に大きな値や小さな値、いわゆる外れ値の影響を受けやすいという点です。外れ値があると、平均二乗誤差の値が大きく歪められてしまい、モデルの正確さを正しく評価できない可能性があります。例えば、ほとんどのデータが予測値に近い値を取っていても、一つだけ大きく外れた値があると、平均二乗誤差は大きくなってしまいます。
そのため、平均二乗誤差だけでモデルの良し悪しを判断するのではなく、他の指標と組み合わせて使うことが重要です。例えば、外れ値の影響を受けにくい指標として、平均絶対誤差や中央絶対誤差などがあります。これらの指標も併用することで、モデルの性能をより多角的に評価することができます。
まとめると、平均二乗誤差は計算が簡単で大きな誤差を重視できるという利点がありますが、外れ値に弱いという欠点も持っています。データの特性を理解し、他の指標も活用しながら、状況に応じて適切に使い分けることが大切です。
| 項目 | 説明 |
|---|---|
| 定義 | 実際の値と予測値の差を二乗して平均したもの |
| 意味 | 値が小さいほど、予測が正確 |
| 計算方法 | 各データの(実際値 – 予測値)^2 の合計 / データ数 |
| メリット | 計算が容易 大きな誤差を強調 |
| デメリット | 外れ値の影響を受けやすい |
| 注意点 | 他の指標(平均絶対誤差、中央絶対誤差など)と組み合わせて使う |
