平均二乗誤差:機械学習の基本指標

AIを知りたい
先生、「MSE」ってなんですか?よく聞くんですけど、ちゃんと意味がわからないんです。

AIエンジニア
MSEは「平均二乗誤差」のことだよ。機械学習で、予測した値がどれくらい正解から外れているかを測るのに使うんだ。

AIを知りたい
外れ具合を測る…ですか?具体的にはどう計算するんですか?

AIエンジニア
まず、正解の値と予測した値の差を求める。それを二乗して、たくさんのデータで平均を取ったものがMSEだよ。二乗するから、誤差が大きいほどMSEの値も大きくなるんだ。
MSEとは。
人工知能の分野でよく使われる言葉に「平均二乗誤差」というものがあります。これは統計学や機械学習で使われる計算方法です。簡単に言うと、機械学習で出した予測と本当の値がどれくらい離れているかを測るものです。正解から予測値を引いても、予測値から正解を引いても、どちらで計算しても構いません。二乗するおかげで、誤差がプラスかマイナスかは関係なくなります。
平均二乗誤差とは

平均二乗誤差(へいきんじじょうごさ)とは、機械学習の分野で、作った模型の良し悪しを測る物差しの一つです。この物差しは、模型が予想した値と、実際に起きた値との違いを測ることで、模型の精度を確かめることができます。
具体的には、まず模型が予想した値と、実際に起きた値との差を計算します。この差を「誤差」と言います。次に、この誤差を二乗します。二乗する理由は、誤差が正負どちらの場合でも、その大きさを正の値として扱うためです。そして、全てのデータ点における二乗した誤差を合計し、データの個数で割ります。こうして得られた値が平均二乗誤差です。
平均二乗誤差の値が小さければ小さいほど、模型の予想が実際の値に近いことを示し、模型の精度が高いと言えます。逆に、値が大きければ大きいほど、模型の予想が実際の値からかけ離れており、模型の精度が低いと言えます。
例えば、来月の商品の売り上げを予想する模型を作ったとします。この模型を使って来月の売り上げを予想し、実際に来月が終わった後に、模型が予想した売り上げと、実際の売り上げを比較します。もし平均二乗誤差が小さければ、その模型は来月の売り上げを精度良く予想できたと言えるでしょう。
平均二乗誤差は、様々な種類の模型の精度を測るために使えます。例えば、商品の売り上げ予想以外にも、株価の予想や天気の予想など、様々な場面で使われています。また、複数の模型の性能を比べる時にも役立ちます。複数の模型で平均二乗誤差を計算し、その値を比較することで、どの模型が最も精度が高いかを判断できます。そして、より精度の高い模型を選ぶことで、より正確な予想を行うことができます。
| 用語 | 説明 |
|---|---|
| 平均二乗誤差 | 機械学習モデルの精度を評価するための指標。モデルの予測値と実測値の差の二乗の平均。 |
| 誤差 | モデルの予測値と実測値の差。 |
| 計算方法 | 1. 予測値と実測値の差(誤差)を計算する。 2. 各誤差を二乗する。 3. 全ての二乗誤差を合計する。 4. データの個数で割る。 |
| 評価 | 値が小さいほど、モデルの精度が高い。 |
| 使用例 | 商品の売上予測、株価予測、天気予測など。複数のモデルの性能比較。 |
計算方法

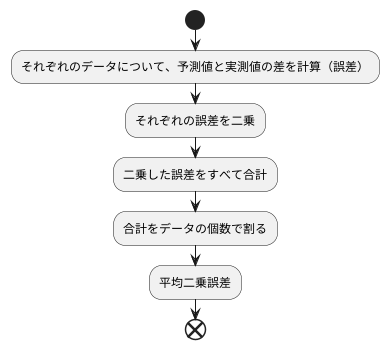
平均二乗誤差を計算する方法はとても簡単です。いくつかの段階に分けて、その手順を詳しく説明します。まず、それぞれのデータを見て、機械学習モデルが予測した値と実際に観測された値の差を計算します。この差が誤差です。誤差は、予測値が観測値よりも大きければ正の値、小さければ負の値になります。
次に、計算したそれぞれの誤差を二乗します。誤差を二乗するのは、正の誤差と負の誤差が互いに打ち消し合って、全体の誤差が小さく見えてしまうのを防ぐためです。二乗することで、すべての誤差は正の値になり、誤差の大きさだけが評価されます。
最後に、二乗した誤差をすべて足し合わせ、その合計をデータの個数で割ります。こうして得られた値が平均二乗誤差です。これは、誤差の二乗の平均値を表しています。
数式を使って説明すると、データの個数を「データの数」と表し、それぞれのデータについて「予測値」と「実測値」がある場合、平均二乗誤差は次の式で計算できます((予測値 – 実測値)² の合計)/ データの数。「合計」とは、すべてのデータについて計算した値を足し合わせることです。
具体的な例を挙げると、3つのデータがあり、それぞれの予測値が10, 20, 30で、実測値が12, 18, 32だとします。まず、それぞれの誤差を計算します。最初のデータでは10 – 12 = -2、次のデータでは20 – 18 = 2、最後のデータでは30 – 32 = -2となります。次に、それぞれの誤差を二乗します。(-2)² = 4、2² = 4、(-2)² = 4となります。これらの二乗した誤差を合計すると、4 + 4 + 4 = 12です。最後に、この合計をデータの数である3で割ります。12 / 3 = 4です。よって、この場合の平均二乗誤差は4となります。
他の指標との違い

機械学習の分野では、作った模型の良し悪しを測る物差しがいくつかあります。その中で、平均二乗誤差はよく使われる物差しの一つですが、他にもいくつか種類があります。それぞれの特徴を理解し、目的に合った物差しを選ぶことが大切です。
平均二乗誤差は、予測と実際の値の差を二乗したものの平均です。このため、大きな違いがより強調されます。例えば、ある商品の売れ行きを予測する際に、大きく外れた予測は、小さな外れよりも大きな損失に繋がるため、平均二乗誤差を用いることで、大きな外れをより重視した評価ができます。
一方、平均絶対誤差は、予測と実際の値の差の絶対値の平均です。こちらは、二乗しないため、大きな違いも小さな違いも、そのままの大きさで評価されます。全体的な予測のずれ具合を知りたい場合に適しています。例えば、日々の気温の予測では、極端な外れ値よりも、全体の平均的なずれ具合が重要になる場合もあるでしょう。このような場合には、平均絶対誤差が役に立ちます。
二乗平均平方根誤差は、平均二乗誤差の平方根をとったものです。これは、元のデータと同じ単位で誤差を表現できるため、結果を理解しやすいという利点があります。例えば、身長の予測で、二乗平均平方根誤差を用いれば、平均的にどれくらい予測がずれているかをセンチメートル単位で把握できます。
このように、それぞれの物差しには異なる特徴があります。予測したいものや、重視したい点に応じて、適切な物差しを選び、より良い模型作りに役立てましょう。
| 指標 | 計算方法 | 特徴 | 用途例 |
|---|---|---|---|
| 平均二乗誤差 (MSE) | 予測値と実測値の差の二乗の平均 | 大きな誤差を強調 | 売れ行き予測(大きな誤差が大きな損失に繋がる場合) |
| 平均絶対誤差 (MAE) | 予測値と実測値の差の絶対値の平均 | 誤差をそのままの大きさで評価 | 気温予測(全体の平均的なずれ具合を知りたい場合) |
| 二乗平均平方根誤差 (RMSE) | 平均二乗誤差の平方根 | 元のデータと同じ単位で誤差を表現 | 身長予測(センチメートル単位での誤差把握) |
活用事例

平均二乗誤差は、連続した値を予想する機械学習の仕事で広く使われています。この仕事は、回帰問題と呼ばれ、将来の値を予測するために使われます。いくつかの具体的な例を見ていきましょう。
まず、株価予想です。過去の株価の動きを元に、この先の株価がどうなるかを予想する計算式を作ります。この計算式がどれくらい正確なのかを確かめるために、平均二乗誤差を使います。実際の株価と計算式が出した予想値の差を二乗して平均することで、予想の正確さを評価します。
次に、売上の予想です。過去の売上の記録や市場の状況などを考えて、これからの売上がどれくらいになるのかを予想する計算式を作ります。ここでも、平均二乗誤差を使って、計算式の正確さを評価します。過去の売上と予想値の差が小さければ小さいほど、計算式は正確だと言えます。
さらに、商品の需要予想です。過去の需要の記録や経済の状況などを元に、これからの商品の需要がどれくらいになるのかを予想する計算式を作ります。平均二乗誤差は、この計算式の正確さを評価するのにも役立ちます。過去の需要と予想値の差が小さければ小さいほど、計算式は信頼できます。
このように、平均二乗誤差は、株価予想、売上予想、需要予想など、様々な場面で使われています。これらの予想は、企業が今後の計画を立てる上で非常に重要です。平均二乗誤差を使って計算式の正確さを評価することで、より確かな情報に基づいた意思決定を行うことができます。つまり、平均二乗誤差は、企業の経営判断を助ける大切な道具として活躍しているのです。
| 用途 | 説明 |
|---|---|
| 株価予想 | 過去の株価データから将来の株価を予測するモデルの精度を評価。実際の株価と予測値の差を二乗して平均することで誤差を計算。 |
| 売上予想 | 過去の売上データや市場状況から将来の売上を予測するモデルの精度を評価。実際の売上と予測値の差を二乗して平均することで誤差を計算。 |
| 需要予想 | 過去の需要データや経済状況から将来の商品需要を予測するモデルの精度を評価。実際の需要と予測値の差を二乗して平均することで誤差を計算。 |
長所と短所

平均二乗誤差には、利点と欠点の両方が存在します。計算の容易さと広く知られている点が大きな利点です。数式も比較的単純で、多くの統計ソフトやプログラミング言語で簡単に計算できます。そのため、データ分析の初心者から専門家まで、幅広い人が手軽に利用できます。また、一般的に理解されている指標であるため、分析結果を他の人と共有したり、議論したりする際にも便利です。さらに、誤差を二乗することで、大きな誤差をより重視するという特徴があります。これは、モデルの予測精度を高める上で重要な役割を果たします。小さな誤差は二乗してもそれほど大きな値にはなりませんが、大きな誤差は二乗すると非常に大きな値になります。そのため、平均二乗誤差を最小化しようとすると、モデルは大きな誤差を減らす方向に学習され、結果として予測精度が向上するのです。
しかし、平均二乗誤差は外れ値の影響を受けやすいという欠点も持っています。外れ値とは、他のデータから大きく離れた異常値のことです。平均二乗誤差は誤差を二乗するため、もし外れ値が含まれていると、その値が二乗されて非常に大きな値となり、全体の誤差を押し上げてしまいます。例えば、商品の売上予測モデルを構築する際に、ある日に通常では考えられないほどの売上があったとします。この場合、その日のデータは外れ値とみなされ、平均二乗誤差に大きな影響を与えてしまう可能性があります。結果として、モデルの真の性能を正しく評価できなくなってしまうのです。このような場合は、外れ値を除外したり、外れ値の影響を受けにくい他の指標を検討したりするなどの対策が必要です。また、平均二乗誤差は、誤差の大きさを直感的に理解しにくいという問題点もあります。これは、誤差が二乗されているため、元のデータの単位とは異なる単位で表されることが原因です。例えば、商品の価格を予測するモデルで平均二乗誤差を計算した場合、その値は価格の二乗の単位で表されます。そのため、誤差の大きさを感覚的に捉えにくく、モデルの性能を評価する上で不便な場合があります。誤差の大きさを直感的に理解したい場合は、二乗平均平方根誤差などの別の指標を用いるのが適切です。
| 項目 | 内容 |
|---|---|
| 利点 |
|
| 欠点 |
|
