局所最適解とは?:機械学習の落とし穴

AIを知りたい
先生、『局所最適解』って、何ですか? 最適解とどう違うんですか?

AIエンジニア
いい質問だね。最適解とは、一番良い答えのことだよ。たとえば、山を一番高いところに登ることが目的だとすると、山頂が一番良い答え、つまり最適解になる。局所最適解は、山頂以外にも、周りの景色から見て高いところ、つまり、一見最適解のように見える場所のことだよ。本当の山頂ではないけれど、近くでは一番高いから、そこで満足してしまうんだ。

AIを知りたい
なるほど。じゃあ、本当の山頂、つまり最適解にたどり着くにはどうすればいいんですか?

AIエンジニア
そうだね。一度登った山を下りて、別の山を登ってみたり、もっと遠くまで見渡して高い山がないか探したりする必要があるね。AIの学習では、一度決めかけた答えを疑って、違う答えを探してみる工夫が必要になるんだよ。
局所最適解とは。
人工知能の分野でよく使われる「局所最適解」という言葉について説明します。「局所最適解」とは、勾配降下法という手法で現れる、いわば「偽物の最適解」のことです。特別な工夫をしないまま計算を進めると、この「偽物の最適解」に捕まってしまう可能性が高くなります。これを避けるためには、学習率と呼ばれる値を大きくするなどの対策が必要です。
最適解の種類

機械学習の目的は、与えられた情報から最も良い予測をするための計算方法、つまり模型を組み立てることです。この模型作りで大切なのは、模型の良し悪しを測るための物差し、つまり評価の基準となる数値を定めることです。この数値は、模型の出来が悪いほど大きくなり、良いほど小さくなるように設定します。もしくは、反対に、良いほど数値が大きくなるように設定する場合もあります。目指すのは、この数値が最も小さくなる、あるいは最も大きくなる模型を見つけることです。この数値が最も良い値をとる点を最適解と呼びます。最適解には、大きく分けて二つの種類があります。一つは全体最適解、もう一つは局所最適解です。
全体最適解とは、あらゆる模型の中で最も評価数値が良い、つまり一番良い模型に対応する点です。例えるなら、広い山脈の中で一番高い山頂のようなものです。この山頂に辿り着けば、これ以上高い場所は他にないと断言できます。一方、局所最適解とは、周りを見渡した限りでは一番良いように見えるものの、実際にはもっと良い点が存在する可能性がある点です。これは、山脈の途中で登った小さな丘の頂上のようなものです。その丘の頂上にいる限り、周りを見渡しても他に高い場所はありません。しかし、山脈全体で見れば、もっと高い山頂が他に存在するかもしれません。このように、局所最適解は、全体で見れば最適ではないものの、その周辺だけを見ると最適に見えるため、本当の最適解を見つけるための邪魔になることがあります。機械学習では、この局所最適解という罠に囚われず、真の全体最適解を見つけ出す方法が常に模索されています。目指すは山脈で一番高い山頂であり、途中の小さな丘で満足して立ち止まってはいけません。
勾配降下法と局所最適解

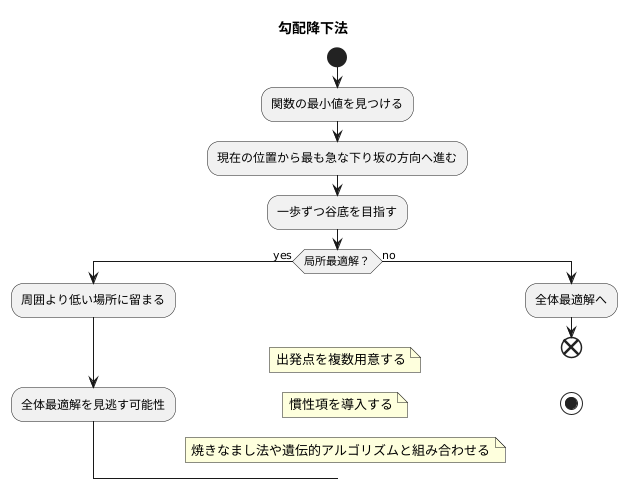
機械学習の分野では、最適化は重要な役割を担っています。数ある最適化手法の中でも、勾配降下法は広く利用されています。この手法は、関数の値を最小にする入力値を見つけることを目的としています。具体的には、現在の位置から見て最も急な下り坂の方向へ進むことで、最小値を探し出します。まるで山の斜面を下るように、一歩ずつ谷底を目指していくイメージです。しかし、勾配降下法には、局所最適解に陥りやすいという欠点があります。
局所最適解とは、全体で見れば最も低い点ではないものの、周囲と比べて低い点のことです。例えば、複数の谷がある地形を考えてみましょう。勾配降下法は、現在地から見て最も急な斜面を下っていきます。しかし、その斜面が最も深い谷底へ続いているとは限りません。小さな谷に降りてしまうと、周囲より低い場所に留まり、そこから抜け出せなくなる可能性があります。つまり、全体で見ればもっと低い場所(全体最適解)があるにも関わらず、局所的な最適解に捕らわれてしまうのです。これは、勾配降下法が局所的な情報、つまり現在地の周りの傾きだけを頼りに探索を行うため、全体像を把握できないという弱点に起因しています。
この問題を回避するために、様々な工夫が凝らされています。例えば、出発点を複数用意することで、異なる谷を探索し、全体最適解を見つけやすくする方法があります。また、慣性項を導入することで、局所最適解から抜け出す勢いを与える方法もあります。他にも、焼きなまし法や遺伝的アルゴリズムといった、より高度な最適化手法と組み合わせることで、局所最適解の問題を軽減することも可能です。勾配降下法は強力な手法ですが、その特性を理解し、適切に利用することが重要です。
局所最適解への対策

機械学習の目的は、与えられたデータから最適なモデルを見つけ出すことです。しかし、モデルの学習過程において、全体の中で最も良い解(全体最適解)ではなく、局所的に最も良い解(局所最適解)に捕まってしまう場合があります。これは、山登りで最も高い頂上(全体最適解)を目指しているのに、途中の小さな丘(局所最適解)で立ち往生してしまうようなものです。
この局所最適解の問題に対処するためには、様々な工夫が必要です。その一つとして、学習の進み具合を調整する「学習率」の制御が挙げられます。学習率とは、一度にどれだけの大きさでモデルのパラメータを更新するかを決める値です。この値が小さすぎると、学習の進みが遅く、なかなか最適解にたどり着けません。まるで、一歩一歩を小さくしすぎて、頂上までなかなかたどり着けないようなものです。逆に、学習率が大きすぎると、最適解を通り過ぎてしまい、解が振動したり、さらに悪い方向へ進んでしまう可能性があります。これは、一歩が大きすぎて、頂上を飛び越えてしまうようなものです。
適切な学習率を設定することが、局所最適解を避け、全体最適解へと近づく鍵となります。しかし、最適な学習率は、扱う問題の性質やデータの複雑さによって大きく変わるため、試行錯誤を通して最適な値を見つけることが重要です。ちょうど、山の地形に合わせて歩く歩幅を変える必要があるように、問題に合わせて学習率を調整する必要があるのです。
その他にも、様々な初期値から学習を開始する方法や、確率的な要素を加える方法など、局所最適解を回避するための様々な手法があります。これらの手法を組み合わせることで、より確実に全体最適解に近づき、精度の高いモデルを構築することができます。
多様な初期値の利用

坂を下るようにして一番低い場所を探す方法は、探索の出発点によって、最終的にたどり着く場所が変わります。この出発点を初期値と言います。もし初期値が、全体の中で一番低い場所ではなく、周囲より低いだけの場所の近くに設定されていると、その周囲より低いだけの場所に落ち着いてしまうことがよくあります。
これを避けるには、様々な初期値から探索を始めることが重要です。複数の異なる出発点から探索を始めることで、それぞれ違った場所にたどり着き、それらを比べることで本当に一番低い場所を見つけられる可能性が高まります。
例えとして、山の頂上を探すことを考えてみましょう。山の頂上は、全体で一番高い場所です。しかし、山には頂上以外にも、周囲より高い場所がたくさんあります。もし、このような周囲より高いだけの場所から登り始めると、本当の頂上ではなく、その場所に留まってしまうかもしれません。
より高い頂上を見つけるためには、様々な場所から山登りを始める必要があります。麓の様々な地点から登り始め、どの地点から登ると一番高い山頂にたどり着けるかを試すのです。
同様に、坂を下る方法でも、様々な初期値を試すことで、周囲より低いだけの場所に落ち着くことなく、全体で一番低い場所、つまり最適な解を見つけられる可能性が高まります。複数の初期値を試すことは、より良い結果を得るための重要な戦略と言えるでしょう。
| 探索の種類 | 目的 | 問題点 | 解決策 |
|---|---|---|---|
| 坂を下る探索 (最小値探索) | 一番低い場所を探す | 初期値が局所最適解(周囲より低いだけの場所)の近くに設定されていると、そこに落ち着いてしまう | 様々な初期値から探索を始める |
| 山登り探索 (最大値探索) | 一番高い場所(山頂)を探す | 初期値が局所最適解(周囲より高いだけの場所)の近くに設定されていると、そこに落ち着いてしまう | 麓の様々な地点から登り始める |
より高度な最適化手法

様々な計算の難しさや速さをより良くするために、色々な工夫が考えられています。その中でも、最適化手法は重要な役割を担っています。よく知られた手法の一つに、勾配降下法があります。これは、山の斜面を下るように、少しずつ最適な値を探していく方法です。しかし、この方法だけでは、山の麓にある谷底のような場所に留まってしまい、真に一番低い場所を見つけられないことがあります。
このような問題を解決するために、より高度な最適化手法が開発されてきました。例えば、モーメンタム法は、過去の動きの勢いを利用することで、小さな谷底に捕らわれずに、より低い場所を目指します。これは、まるでボールが斜面を転がるように、勢いをつけて進むイメージです。また、確率的勾配降下法は、全体のデータから一部だけを抜き出して計算を行います。これは、計算の負担を軽くするだけでなく、偶然性を取り入れることで、思いがけない良い結果につながる可能性も秘めています。まるで、宝探しのように、色々な場所を少しずつつ探ってみるイメージです。
さらに、自然界の現象からヒントを得た手法もあります。遺伝的アルゴリズムは、生物の進化のように、良い特徴を持つものを掛け合わせて、より良い解を世代交代で探していきます。また、焼きなまし法は、金属を熱してからゆっくり冷やすことで、内部の構造を安定させるように、最初は大きく変化させて、徐々に変化を小さくしていくことで最適な解を見つけます。これらの手法は、計算に時間はかかりますが、複雑な問題に対してより良い解を見つける可能性を高めます。
最適な手法は、扱う問題の種類やデータの量によって異なります。そのため、それぞれの特性を理解し、適切な手法を選ぶことが重要です。
| 手法 | 説明 | イメージ |
|---|---|---|
| 勾配降下法 | 山の斜面を下るように、少しずつ最適な値を探していく方法。ただし、局所解に陥る可能性がある。 | 山の麓の谷底 |
| モーメンタム法 | 過去の動きの勢いを利用し、局所解に陥りにくくする。 | ボールが斜面を転がる |
| 確率的勾配降下法 | データの一部を利用して計算し、計算コストを削減。偶然性により良い解に到達する可能性も。 | 宝探し |
| 遺伝的アルゴリズム | 生物の進化のように、良い特徴を持つものを掛け合わせて、より良い解を世代交代で探す。 | 生物の進化 |
| 焼きなまし法 | 最初は大きく変化させて、徐々に変化を小さくしていくことで最適な解を見つける。 | 金属の焼きなまし |
