線形回帰:機械学習の基礎

AIを知りたい
先生、線形回帰って、データを直線で近似して表すことですよね?でも、実際のデータって、必ずしも直線上に並ばないと思うんですが、どうするんですか?

AIエンジニア
いい質問だね!その通り、実際のデータは必ずしも直線上には並びません。線形回帰では、データに最も近い直線を探すんだけど、完璧に一致させるのは難しい。そこで、直線とデータのずれ(誤差)をなるべく小さくするように線を引くんだ。その方法の一つが最小二乗法だよ。

AIを知りたい
最小二乗法…誤差を小さくするんですね。でも、誤差を小さくする方法は他にもありそうですよね? なぜ最小二乗法を使うんですか?

AIエンジニア
そうだね、他の方法もあるよ。最小二乗法は、計算が比較的簡単で、多くの場合で良い結果が得られるから広く使われているんだ。それに、数学的な裏付けもしっかりしているから、信頼性も高いんだよ。
線形回帰とは。
人工知能でよく使われる「線形回帰」という言葉について説明します。線形回帰とは、たくさんのデータに線を引いて、データの特徴を表そうとする方法です。線を引くときは、中学校で習うような “y = ax + b” の形を使います。ただし、この線は全てのデータにぴったり合うとは限りません。データと線の間にズレ(誤差)が出てしまうこともあります。線形回帰では、このズレをなるべく小さくするために「最小二乗法」という方法がよく使われます。線形回帰について、もっと詳しく知りたい、実際にプログラミングで試したいという方は、公開中の記事をご覧ください。記事では、プログラミング言語Pythonを使った例を載せていて、コードを実際に動かせるようになっていますので、より深く理解することができます。機械学習の入門として「線形回帰」をPythonとNumPyで試してみましょう。
線形回帰とは

線形回帰とは、物事の関係性を直線で表そうとする統計的な方法です。身の回りには、様々な関係性を持った物事が存在します。例えば、気温とアイスクリームの売上には関係があると考えられます。気温が高い日はアイスクリームがよく売れ、気温が低い日はあまり売れないといった具合です。このような関係を、線形回帰を使って直線で近似することで、一方の値からもう一方の値を予想することができます。
直線は数式で「結果 = 傾き × 説明 + 切片」と表されます。ここで、「結果」は予想したい値(アイスクリームの売上)、「説明」は既に分かっている値(気温)です。「傾き」と「切片」は直線の形を決める数値で、これらを適切に決めることで、観測されたデータに最もよく合う直線を引くことができます。
線形回帰の目的は、観測データに最もよく合う「傾き」と「切片」を見つけることです。しかし、全ての点をぴったり直線上に載せることは、多くの場合不可能です。直線とデータ点の間には必ずずれが生じ、これを「誤差」といいます。線形回帰では、この誤差をできるだけ小さくするように直線を決定します。誤差を小さくする方法として、「最小二乗法」という方法がよく使われます。これは、各データ点と直線との間の距離の二乗を全て足し合わせ、この合計値が最小になるように「傾き」と「切片」を調整する方法です。
線形回帰は様々な分野で使われています。経済の分野では、商品の需要予想や株価の分析に役立ちます。医療の分野では、病気にかかる危険性を予想するのに使われます。また、販売促進の分野では、顧客の行動を分析する際にも利用されています。線形回帰は、機械学習という技術の中でも基本的な考え方であり、これを理解することは、より高度な機械学習を学ぶための大切な一歩となります。
| 項目 | 説明 |
|---|---|
| 線形回帰 | 物事の関係性を直線で表す統計的方法。一方の値からもう一方の値を予想する。 |
| 直線の式 | 結果 = 傾き × 説明 + 切片 |
| 結果 | 予想したい値(例:アイスクリームの売上) |
| 説明 | 既に分かっている値(例:気温) |
| 傾き・切片 | 直線の形を決める数値。データに合うよう調整。 |
| 誤差 | 直線とデータ点の間のずれ。 |
| 最小二乗法 | 誤差の二乗の合計を最小にする方法。 |
| 応用例 | 経済(需要予想、株価分析)、医療(危険性予測)、販売促進(顧客行動分析)など。 |
| 機械学習 | 線形回帰は基本的な考え方。 |
最小二乗法

たくさんの点々が散らばる図を想像してみてください。これらの点は、集めたデータを表しています。例えば、ある商品の値段と売れた数の関係を表しているかもしれません。これらの点に、一本の直線を引いて、データ全体の傾向を表したいとします。このとき、どの直線が最もデータに「よく合う」と言えるでしょうか? それを決めるための方法の一つが、最小二乗法です。
最小二乗法は、それぞれの点と直線との間の距離を考えて、その距離の二乗をすべて足し合わせた値を最小にする直線を探します。点と直線との距離は、直線に対して垂直に線を引いたときの長さで、「残差」と呼ばれます。この残差は、実測値と予測値の差を表しています。直線を少し傾けたり、上下にずらしたりすると、それぞれの点との距離、つまり残差が変わります。最小二乗法では、すべての点における残差の二乗の合計が最も小さくなるように、直線の傾きと切片(縦軸との交点)を決めます。
なぜ二乗するのでしょうか? それは、残差に正負の値が混ざっていると、互いに打ち消しあってしまい、全体としてのずれを正しく評価できないからです。二乗することで、すべての残差を正の値に変換し、ずれの大きさを適切に評価できます。また、二乗することにより、大きなずれを持つ点の影響がより強く反映されるため、外れ値の影響を考慮した直線を引くことができます。
最小二乗法は、計算方法が分かりやすく、最適な解を一つに決めることができるので、広く使われています。計算に複雑な処理が必要なく、電卓や表計算ソフトでも計算できます。また、データに含まれるばらつき(ノイズ)の影響を減らし、より確かな予測をするのに役立ちます。最小二乗法は、統計や機械学習の分野で、様々な場面で使われている、基本的な手法です。
| 項目 | 説明 |
|---|---|
| 目的 | 散らばるデータ点の全体傾向を表す最適な直線を見つける |
| 方法 | 最小二乗法 |
| 最小二乗法とは | 各データ点と直線間の距離(残差)の二乗和を最小にする直線を探す方法 |
| 残差 | データ点と直線間の垂直距離、実測値と予測値の差 |
| 二乗する理由 |
|
| 利点 |
|
| 応用分野 | 統計、機械学習 |
実践的な活用

直線的な関係を表す数式、線形回帰は、学ぶだけでなく実際に使ってみることで、その真価が分かります。頭で理解するだけでなく、手を動かすことで、より深く理解を深めることができるのです。実践的な活用方法を学ぶのに最適な道具として、プログラミング言語のパイソンと、その数値計算を行うための追加の道具であるナムパイがあります。
パイソンは、機械学習の分野で広く使われているプログラミング言語です。色々な機能を追加できるたくさんの道具が用意されているため、様々な作業を効率的に行うことができます。線形回帰のような計算を行う際にも、パイソンは非常に役立ちます。ナムパイは、パイソンで高度な計算を行うための追加の道具です。線形代数や統計処理といった、線形回帰に必要な計算を効率的に行うための機能が豊富に揃っています。
これらの道具を使うことで、データの読み込みから、不要な部分を取り除く作業、線形回帰のモデルを作る学習、そして将来の値を予測する作業まで、一連の流れをスムーズに行うことができます。実際にデータを分析してみることで、机上の学習だけでは得られない、実践的な知識や技術を身につけることができます。
インターネット上には、パイソンのプログラムを使って線形回帰を学ぶことができる記事が公開されています。これらの記事では、実際にプログラムを実行しながら学ぶことができるので、より深い理解を得ることができます。プログラムを実行するための環境も提供されているため、すぐに学習を始めることができます。線形回帰についてもっと深く理解したい、実践的なスキルを身につけたいと考えている方には、ぜひこれらの記事を活用することをお勧めします。実際に手を動かしながら学ぶことで、より効果的に線形回帰を理解し、データ分析の能力を高めることができるでしょう。
| テーマ | 説明 |
|---|---|
| 線形回帰 | 直線的な関係を表す数式。実践的な活用が重要。 |
| Python | 機械学習で広く使われているプログラミング言語。線形回帰の計算にも役立つ。豊富なツールが利用可能。 |
| NumPy | Pythonで高度な計算を行うための追加ツール。線形代数や統計処理に強い。 |
| 実践的学習 | データの読み込み、不要部分の除去、モデル作成、予測まで一連の流れをPythonとNumPyで実行可能。 |
| オンラインリソース | Pythonを使った線形回帰学習記事が利用可能。実行環境も提供。 |
より高度な手法

機械学習の世界への入り口として、線形回帰はまさにうってつけの手法です。しかし、現実世界で見かけるデータは複雑に入り組んでいることが多く、線形回帰だけでは対応しきれない場面も出てきます。例えば、データの分布が曲線を描いている場合や、たくさんの変数が複雑に関係しあっている場合などです。このような状況では、線形回帰で予測しようとしても、なかなか思うような精度が得られないことがあります。
では、どうすればいいのでしょうか?そのような時にこそ、多項式回帰やサポートベクターマシン、ランダムフォレストといった、より高度な機械学習の手法の出番です。これらの手法は、線形回帰よりも複雑なモデルを作り上げることができ、より高い精度で未来を予測することが可能になります。例えば、多項式回帰は、曲線を描くデータの分布にも対応できるため、線形回帰では捉えきれなかった関係性を表現できます。サポートベクターマシンは、高次元空間でデータを分類することに得意であり、複雑な関係性を持つデータにも対応できます。ランダムフォレストは、多数の決定木を組み合わせることで、よりロバストで精度の高い予測を実現します。
ただし、これらの高度な手法には、モデルの解釈が難しくなるという側面も持ち合わせています。線形回帰は、変数と結果の関係が分かりやすい一方、高度な手法では、モデルが複雑であるがゆえに、なぜそのような予測結果になったのかを理解するのが難しくなる場合があります。
しかし、線形回帰をしっかりと学ぶことは、これらの高度な手法を理解するための土台作りに繋がります。線形回帰で学ぶ基本的な考え方や手法は、他の機械学習の手法にも応用できる共通の知識です。ですから、線形回帰をしっかりと理解しておくことは、機械学習全体を理解する上で非常に大切と言えるでしょう。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 線形回帰 | 単純な線形関係をモデル化 | 解釈が容易 | 複雑なデータには対応できない |
| 多項式回帰 | 曲線を描くデータに対応 | 線形回帰より複雑な関係性を表現可能 | モデルの解釈が難しい場合がある |
| サポートベクターマシン | 高次元空間でデータを分類 | 複雑な関係性を持つデータに対応可能 | モデルの解釈が難しい場合がある |
| ランダムフォレスト | 多数の決定木を組み合わせる | ロバストで精度の高い予測 | モデルの解釈が難しい場合がある |
まとめ

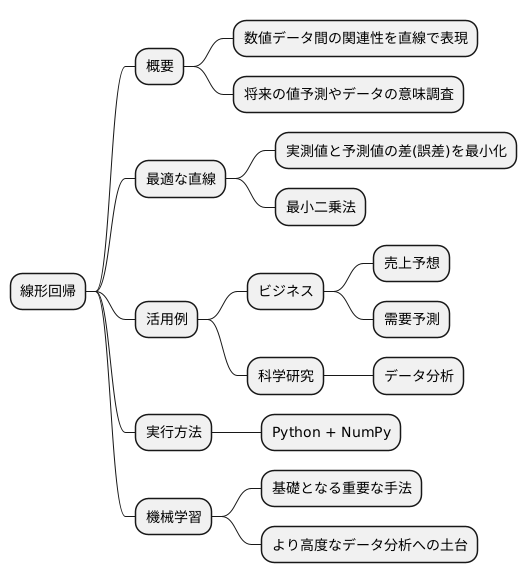
まとめとして、線形回帰は情報を取り扱う様々な場面で欠かせない手法と言えます。この手法は、数値データ間の関連性を直線で表すことで、将来の値を予想したり、データの持つ意味を調べたりすることを可能にします。
線形回帰の肝となるのは、最適な直線を見つけることです。この直線は、実測値と予測値の差である誤差を最小にするように求められます。この計算には、最小二乗法と呼ばれる手法が広く使われています。最小二乗法を用いることで、誤差を極力抑え、精度の高い予測を実現できます。
線形回帰は、様々な分野で活用されています。例えば、会社の売上予想や商品の需要予測といったビジネスの場面はもちろん、科学研究におけるデータ分析にも広く応用されています。線形回帰は、これらの分野での発展に大きく貢献していると言えるでしょう。
実際に線形回帰を試してみるには、プログラミング言語のPythonとその数値計算ライブラリであるNumPyが便利です。これらの道具を使うことで、手軽に線形回帰を実行し、データ分析を行うことができます。机上の理論だけでなく、実際に手を動かすことで、より深く理解を深めることができ、データ分析の技術を高めることができます。
線形回帰は、機械学習という広大な世界の入り口とも言えます。より複雑な機械学習の手法を学ぶための基礎となる重要な手法です。線形回帰をしっかりと理解することで、機械学習全体の仕組みを掴むことができ、さらに高度なデータ分析に挑戦するための土台を築くことができます。これからの学びを進める上で、線形回帰の基礎をしっかりと固めておくことは、大変重要な意味を持ちます。