学習率:最適化の鍵

AIを知りたい
先生、「学習率」ってなんですか?難しそうでよくわからないです。

AIエンジニア
そうですね、少し難しいですね。簡単に言うと、AIが学習する時の「一歩の大きさ」のことです。山を下ることを想像してみてください。一歩が大きすぎると、谷底までたどり着けずに山の斜面を何度も行ったり来たりしてしまいます。逆に一歩が小さすぎると、谷底までたどり着くのに時間がかかってしまいますよね?

AIを知りたい
なるほど!一歩の大きさ、ですか。だから大きすぎても小さすぎてもダメなんですね。ちょうどいい大きさを見つけないといけないんですね。

AIエンジニア
その通りです。AIの学習では、この「ちょうどいい一歩の大きさ」を見つけることがとても重要なんです。これを「学習率」と呼びます。適切な学習率を設定することで、AIは効率よく学習し、より良い結果を得ることができるのです。
学習率とは。
人工知能の分野でよく使われる「学習率」について説明します。学習率とは、機械学習のモデルを訓練する際に、どのくらいパラメータを調整するかを決める値です。具体的には「勾配降下法」といった手法において、一度の学習でどのくらい最適な値に近づけるかを調整するのに使われます。この学習率は大変重要な値で、適切に設定しないと、最も良い結果が得られないことがあります。
学習率とは

機械学習では、たくさんの情報から一番良い答えを見つけることが目的です。コンピュータは、まるで迷路を進むように、何度も試行錯誤を繰り返しながら、少しずつ正しい答えに近づいていきます。この試行錯誤の進み具合を調整するのが「学習率」です。
学習率は、情報から得られたヒントをもとに、どのくらい答えを修正するかを決める数字です。これは、山の頂上を目指す登山家が、一歩どれくらいの距離を進むかを決めるのと似ています。大きな一歩で早く進もうとすると、頂上を通り過ぎてしまうかもしれません。逆に、小さすぎる一歩では、なかなか頂上にたどり着けません。
学習率が大きすぎると、最適な答えを通り過ぎてしまい、いつまでも正しい答えにたどり着けないことがあります。まるで、振り子が大きく揺れすぎて、なかなか中心で静止できないようなものです。逆に、学習率が小さすぎると、正しい答えに近づくのが非常に遅く、膨大な時間がかかってしまいます。これは、登山家が非常にゆっくりとしたペースでしか登らないため、頂上に着くまでに日が暮れてしまうようなものです。
そのため、適切な学習率を設定することが非常に重要です。適切な学習率は、扱う問題によって異なります。複雑な問題では、慎重に小さな一歩を刻む必要があり、簡単な問題では、大きな一歩で素早く答えに近づくことができます。最適な学習率を見つけるためには、様々な値を試してみて、一番良い結果が得られるものを選ぶ必要があります。これは、登山家が様々な歩幅を試して、一番効率的に頂上にたどり着ける歩幅を見つけるようなものです。このように、学習率を調整することで、機械学習は効率的に最適な答えを見つけることができます。
| 学習率 | イメージ | 結果 |
|---|---|---|
| 大きすぎる | 山の頂上を通り過ぎる登山家、大きく揺れて静止しない振り子 | 最適な答えを通り過ぎてしまい、正しい答えにたどり着けない |
| 小さすぎる | 非常にゆっくり登る登山家 | 正しい答えに近づくのが遅く、膨大な時間がかかる |
| 適切 | 効率的に頂上にたどり着く登山家 | 効率的に最適な答えを見つけられる |
学習率の重要性

機械学習の分野において、学習の進み具合を調整する役割を担うのが学習率です。この学習率は、まるで登山家が山頂を目指す際に一歩一歩の歩幅を決めるように、機械学習モデルが最適な状態へと近づくための調整役を果たします。適切な学習率を設定することは、山頂への効率的な道のりを見つけることと同じくらい重要です。
もし、学習率の設定が小さすぎるとどうなるでしょうか。これは、登山家が非常に小さな歩幅で山頂を目指そうとするようなものです。一歩一歩は確実に進んでいるものの、山頂に到達するには非常に長い時間がかかってしまいます。機械学習モデルにおいても同様に、学習率が小さすぎると、学習の進みが遅く、膨大な時間を費やしても最適な解にたどり着けない可能性があります。最適な解とは、山頂のようなもので、モデルが目指すべき目標地点です。小さな歩幅では、いつまでたっても目標地点に到達できないかもしれません。
反対に、学習率の設定が大きすぎると、どうなるでしょうか。これは、登山家が大きすぎる歩幅で山頂を目指そうとするようなものです。一歩が大きすぎるため、山頂を飛び越えてしまう可能性があります。機械学習モデルにおいても同様に、学習率が大きすぎると、最適な解を通り過ぎてしまい、学習が不安定になり、良い結果が得られない可能性があります。まるで、山頂を目指していたはずなのに、谷底に落ちてしまうようなものです。
このように、学習率は小さすぎても大きすぎても問題です。最適な学習率を見つけることは、登山家が最適な歩幅を見つけるのと同じくらい重要であり、機械学習モデルを効率的に学習させるためには適切な学習率の設定が不可欠です。そのため、様々な手法を用いて、最適な学習率を探し出す必要があります。
| 学習率 | 登山家に例えると | 機械学習モデルへの影響 |
|---|---|---|
| 小さすぎる | 小さな歩幅で山頂を目指す | 学習の進みが遅く、最適な解にたどり着くのに時間がかかる |
| 大きすぎる | 大きすぎる歩幅で山頂を目指す | 最適な解を通り過ぎてしまい、学習が不安定になり、良い結果が得られない |
| 適切 | 適切な歩幅で山頂を目指す | 効率的に最適な解にたどり着く |
適切な学習率の設定

機械学習を行う上で、学習率の設定は非常に重要です。この値は、学習の進み具合に直接影響を与えます。まるで、山の頂上を目指す登山家が、どの程度の歩幅で進むかを決めるようなものです。最適な歩幅は、山の地形や登山家の体力によって異なり、一概にどれが良いとは言えません。学習率も同様に、扱う問題やデータセットによって最適な値が変わるため、事前に最適な値を知ることは困難です。
では、どのようにして適切な学習率を見つけるのでしょうか。多くの場合、様々な値を試しながら、学習の進み具合を確かめるという地道な作業が必要です。例えば、0.1や0.01といった、よく使われる値から始めてみます。学習の進みが遅いと感じたら、学習率の値を大きくします。逆に、学習がうまく進まず、値が大きく振れてしまう場合は、学習率を小さくします。このように、試行錯誤を繰り返すことで、徐々に最適な値に近づけていくことができます。
また、学習の段階に応じて学習率を調整するという方法も有効です。学習の初期段階では、まだ頂上までの道のりが遠く、大まかな位置で良いので早く進みたいところです。この段階では、大きな学習率を設定することで、効率的に学習を進めることができます。しかし、頂上に近づくにつれて、より正確な位置に移動する必要が出てきます。そこで、徐々に学習率を小さくすることで、最適な解に収束させていくのです。これは、登山家が最初は大きな歩幅で進み、頂上に近づくにつれて歩幅を小さくしていく様子とよく似ています。
最適な学習率の設定は、学習の効率と精度を大きく左右するため、時間をかけて慎重に見極める必要があります。
| 学習率 | 説明 | 登山家に例えると |
|---|---|---|
| 最適な値 | 問題やデータセットによって異なるため、事前に知ることは困難 | 山の地形や登山家の体力によって、最適な歩幅が異なる |
| 値の決め方 | 様々な値を試しながら、学習の進み具合を確かめる(0.1, 0.01などから始める) | 歩幅を変えながら、登り具合を確認する |
| 学習が進みが遅い場合 | 学習率の値を大きくする | 歩幅を大きくする |
| 学習が進まず、値が振れる場合 | 学習率の値を小さくする | 歩幅を小さくする |
| 学習初期 | 大きな学習率を設定 | 最初は大きな歩幅で進む |
| 学習終盤 | 徐々に学習率を小さくする | 頂上に近づくにつれて歩幅を小さくする |
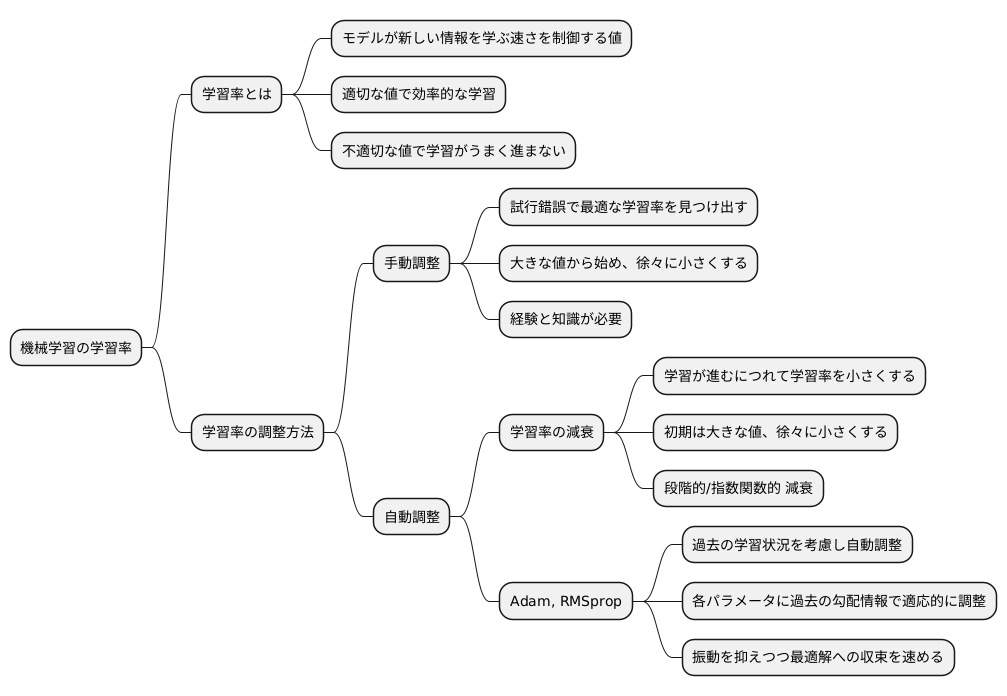
学習率の調整方法

機械学習において、学習の進み具合を左右する重要な要素の一つに学習率があります。これは、モデルが新しい情報をどれくらい速く学ぶかを制御する値です。学習率が適切であれば、効率的に学習を進めることができますが、不適切な場合は学習がうまく進まないことがあります。学習率の調整方法は大きく分けて二つあります。一つは手動で調整する方法、もう一つは自動的に調整する方法です。
手動で調整する場合は、試行錯誤しながら最適な学習率を見つけ出す必要があります。最初は比較的大きな学習率から始め、学習の進み具合を見ながら徐々に小さくしていくのが一般的です。しかし、この方法は手間と時間がかかるため、経験と知識が必要です。
一方、自動的に学習率を調整する方法には様々な手法があります。その一つに「学習率の減衰」があります。これは、学習が進むにつれて学習率を自動的に小さくしていく方法です。学習の初期段階では、大きな学習率を設定することで、大まかな最適解の方向へ素早く近づきます。そして、学習が進むにつれて、学習率を小さくすることで、より精密に最適解へと収束させることができます。学習率の減衰には、段階的に学習率を減らす方法や、指数関数的に減らす方法など、様々な種類があります。
さらに、近年では「Adam」や「RMSprop」といった、より高度な最適化アルゴリズムが広く使われています。これらのアルゴリズムは、過去の学習状況を考慮しながら、自動的に学習率を調整する機能を備えています。これにより、手動で調整する場合に比べて、より効率的に最適解を見つけることができます。具体的には、各々の学習パラメータに対して、過去の勾配の情報を用いて適応的に学習率を調整することで、振動を抑えつつ、最適解への収束を速めます。そのため、これらのアルゴリズムは、様々な機械学習の課題で有効であることが示されています。
勾配降下法との関係

勾配降下法とは、山を下るように関数の最小値を見つける手法です。山を下る人の歩幅に相当するのが学習率です。この歩幅の大きさを調整することで、より速く、確実に谷底、つまり最小値にたどり着くことができます。
勾配降下法は、現在の位置からどの向きに、どのくらい移動すれば関数の値がより小さくなるかを計算します。この計算には関数の勾配を用います。勾配とは、各地点での関数の傾きを表すものです。山で例えるなら、勾配は各地点での斜面の傾きを表します。そして、勾配の反対方向が、最も速く谷底にたどり着く方向になります。
この勾配の反対方向に進む距離を決めるのが学習率です。学習率が小さければ、一歩一歩は慎重になりますが、谷底にたどり着くまでに多くの歩数が必要になります。これは、山を下る人が、非常に小さな歩幅で慎重に下る様子に似ています。谷底にはたどり着けますが、時間がかかります。
反対に、学習率が大きければ、一歩の移動距離は大きくなりますが、谷底を飛び越えてしまう危険があります。これは、山を下る人が、大股で駆け下りる様子に似ています。早く谷底にたどり着ける可能性もありますが、勢い余って谷底を通り越してしまうかもしれません。さらに悪いことに、谷底を何度も行ったり来たりして、いつまでも谷底にたどり着けない可能性もあります。
最適な学習率は、関数の形状や初期位置などによって変化します。そのため、適切な学習率を見つけるためには、様々な値を試す必要があります。適切な学習率を設定することで、勾配降下法は効率的に最小値を見つける強力な道具となります。
| 要素 | 説明 | 山登りアナロジー |
|---|---|---|
| 勾配降下法 | 関数の最小値を見つける手法 | 山を下る |
| 学習率 | 移動の歩幅の大きさ | 歩幅 |
| 小さい学習率 | ゆっくり確実に最小値に近づくが、時間がかかる | 小さい歩幅で慎重に下る |
| 大きい学習率 | 早く最小値に近づける可能性があるが、飛び越えてしまう危険性もある | 大股で駆け下りる |
| 勾配 | 関数の傾き | 斜面の傾き |
