交差エントロピーを学ぶ

AIを知りたい
先生、「交差エントロピー」ってよく聞くんですけど、何なのかイマイチよくわからないんです。教えてもらえますか?

AIエンジニア
そうか、では説明しよう。「交差エントロピー」とは、AIがどれくらい間違っているかを測るためのものさしの一つだ。AIの答えと本当の答えがどれくらい離れているかを計算することで、AIの性能を評価するのに役立つんだ。

AIを知りたい
ものさし…ですか?でも、どうして計算に「対数」とかが出てくるんですか?

AIエンジニア
良い質問だね。対数を使うのは、小さな違いを大きく、大きな違いを小さくして、AIの学習を効率的に進めるためなんだ。例えば、確率が0.1から0.2に変化するのは、0.9から1.0に変化するよりも重要だよね?対数を使うことで、こういった確率の変化の重要度を適切に反映できるんだ。
交差エントロピーとは。
人工知能でよく使われる言葉に「交差エントロピー」というものがあります。これは、どのくらい予測が間違っているかを表す尺度の一つで、最もよく使われているもののひとつです。真の値と予測した値の差を計算し、マイナスの符号をつけたものと考えると良いでしょう。他の尺度と同じように、交差エントロピーの値が小さくなるように調整することで、予測の精度を上げていきます。
交差エントロピーとは

機械学習という、まるで機械が自ら学ぶかのような技術があります。この技術の中でも、学習の良し悪しを判断する大切な指標に、損失関数というものがあります。損失関数は、機械の予測と実際の答えとのずれ具合を数値で表したもので、この数値が小さいほど、機械学習はうまくいっていると考えられます。
交差エントロピーもこの損失関数の一種です。特に、写真を見てそれが猫なのか犬なのかを判断するような、分類問題でよく使われます。例えば、ある写真が猫である確率を機械が80%、犬である確率を20%と予測したとします。そして、実際にはその写真は猫だったとしましょう。この時、交差エントロピーは、機械の予測がどれだけ正解に近かったかを測る尺度となります。
交差エントロピーの計算方法は少し複雑です。まず、正解の確率と機械が予測した確率のそれぞれに、対数を適用します。対数とは、簡単に言うと、ある数を何乗したら元の数になるのかを表す数値です。次に、正解の確率と、それに対応する予測確率の対数を掛け合わせます。猫の場合であれば、正解の確率は100%なので、1と機械が予測した猫である確率80%の対数を掛け合わせます。犬の場合も同様に、正解の確率0%と機械が予測した犬である確率20%の対数を掛け合わせます。最後に、これらの積を全て足し合わせ、符号を反転させます。
交差エントロピーは必ず0以上の値になります。そして、機械の予測が完璧に正解と一致した場合のみ、0になります。つまり、交差エントロピーが小さいほど、機械の予測は正確だと言えるのです。この値を小さくするように機械学習を進めることで、より精度の高い分類が可能になります。
| 用語 | 説明 | 例 |
|---|---|---|
| 機械学習 | 機械が自ら学ぶかのような技術 | – |
| 損失関数 | 機械の予測と実際の答えとのずれ具合を数値で表したもの。小さいほど良い。 | 交差エントロピー |
| 交差エントロピー | 分類問題でよく使われる損失関数。正解の確率と予測確率の対数を用いて計算する。 | 猫の画像を猫と予測:確率80% 犬の画像を犬と予測:確率20% |
| 対数 | ある数を何乗したら元の数になるのかを表す数値 | – |
交差エントロピーの計算方法

交差エントロピーは、機械学習の分野で、予測の正確さを評価する指標として広く使われています。特に、分類問題において、真の確率分布と予測された確率分布の間の差異を測るために利用されます。
計算方法は、段階的に行います。まず、それぞれの事象について、真の確率と予測確率の対数を計算します。真の確率とは、実際にその事象が起こる確率のことです。予測確率とは、機械学習モデルが予測した、その事象が起こる確率のことです。対数は、確率の値を扱いやすくするために用います。
次に、各事象について、真の確率と、対応する予測確率の対数の積を求めます。ある事象の真の確率が高いほど、その事象に対する予測の正確さが重要になります。真の確率が低い事象については、予測が外れても、全体への影響は小さくなります。この計算により、各事象の重要度を考慮した上で、予測の正確さを評価できます。
最後に、これらの積をすべての事象について合計し、その符号を反転させます。合計することで、全ての事象を考慮した全体の予測の正確さを評価できます。符号を反転させるのは、交差エントロピーの値を正の値にするためです。値が小さいほど、予測の正確さが高いことを示します。
具体的な例を挙げると、犬、猫、鳥の三種類の動物を見分ける問題を考えてみましょう。ある写真が犬である真の確率が1、猫である真の確率が0、鳥である真の確率が0とします。これは、写真が実際に犬であることを示しています。モデルが予測した犬である確率が0.8、猫である確率が0.1、鳥である確率が0.1だったとします。この時、交差エントロピーは、-(1×対数(0.8)+0×対数(0.1)+0×対数(0.1)) = -対数(0.8) と計算されます。この値が小さいほど、モデルの予測が正確であると言えます。
| ステップ | 計算内容 | 説明 |
|---|---|---|
| 1 | 真の確率と予測確率の対数を計算 | 確率値を扱いやすくするため |
| 2 | 真の確率と予測確率の対数の積を計算 | 事象の重要度を考慮 |
| 3 | 積の合計値の符号を反転 | 交差エントロピーを正の値にする |
| 動物 | 真の確率 | 予測確率 |
|---|---|---|
| 犬 | 1 | 0.8 |
| 猫 | 0 | 0.1 |
| 鳥 | 0 | 0.1 |
交差エントロピー = -(1 * log(0.8) + 0 * log(0.1) + 0 * log(0.1)) = -log(0.8)
交差エントロピーの利用場面

交差エントロピーとは、異なる確率分布の間の隔たりを測る尺度であり、機械学習の分野、とりわけ分類問題で重要な役割を担っています。具体的には、ある事象について、真の確率分布と機械学習モデルが予測した確率分布の差異を評価するために使われます。この差異が小さければ小さいほど、モデルの予測精度が高いことを意味します。
交差エントロピーが活躍する場面の一つが多クラス分類問題です。多クラス分類とは、三つ以上の選択肢から正解を一つ選ぶ問題を指します。例えば、手書き数字認識を想像してみてください。0から9までの数字が書かれた画像を入力すると、モデルはそれがどの数字であるかを予測します。この場合、正解は一つだけなので、多クラス分類問題と言えます。他にも、画像に写っている物体が猫、犬、鳥のどれなのかを判別する、音声データから発話内容を文字に変換する、といったタスクも多クラス分類に該当します。このような様々な問題において、交差エントロピーはモデルの学習を導くための指標として用いられています。
交差エントロピーは、特にニューラルネットワークの学習において重要な役割を果たします。ニューラルネットワークは、人間の脳の神経回路を模倣した数理モデルであり、学習を通じて複雑なパターンを認識できるようになります。この学習プロセスにおいて、交差エントロピーは損失関数、つまりモデルの予測と正解とのずれを測る指標として使われます。学習の目的は、この損失関数の値を最小化すること、すなわちモデルの予測精度を最大化することにあります。交差エントロピーを用いることで、モデルは予測と正解のずれを効率的に学習し、より正確な予測を行うことができるようになります。さらに、交差エントロピーは、予測の誤りが大きいほど大きな値をとるため、モデルが特定のデータに過度に適合してしまう、いわゆる過学習を防ぐ効果も期待できます。これは、モデルが未知のデータに対しても高い精度で予測を行うために重要な要素です。
| 用語 | 説明 | 例 |
|---|---|---|
| 交差エントロピー | 異なる確率分布の間の隔たりを測る尺度。機械学習、特に分類問題で使用。真の確率分布とモデルの予測分布の差異を評価。 | – |
| 多クラス分類 | 三つ以上の選択肢から正解を一つ選ぶ問題。 | 手書き数字認識(0-9のどれか)、画像認識(猫、犬、鳥のどれか)、音声認識 |
| ニューラルネットワーク | 人間の脳の神経回路を模倣した数理モデル。学習を通じて複雑なパターンを認識。 | – |
| 損失関数 | モデルの予測と正解とのずれを測る指標。交差エントロピーがよく使われる。 | – |
| 過学習 | モデルが特定のデータに過度に適合してしまう現象。未知のデータへの予測精度が低下する。 | – |
交差エントロピーと他の誤差関数の違い

機械学習において、目的関数の最小化は学習の要です。この目的関数の一部を担うのが誤差関数であり、予測と実際の値の差を測る尺度です。様々な誤差関数の中で、交差エントロピーは分類問題で、特に確率予測を扱う場合に多用されます。他の誤差関数、例えば平均二乗誤差などとの違いを理解することは、モデルの性能向上に不可欠です。
平均二乗誤差は、予測値と実測値の差を二乗して平均したものです。これは回帰問題、つまり連続値を予測する問題に適しています。例えば、株価や気温の予測などで、予測値と実測値のずれを数値的に捉えるのに役立ちます。一方、交差エントロピーは、分類問題、特にそれぞれのクラスに属する確率を予測する際に用います。例えば、画像認識で、ある画像が猫である確率、犬である確率などを予測する場合です。この時、単に予測値と実測値の差を見るのではなく、予測された確率分布全体と真の分布との差を評価します。
交差エントロピーの利点の一つは、確率に基づいた予測の良さを評価できる点です。例えば、ある画像が猫であると予測する際、99%の確率で猫と予測したモデルと、51%の確率で猫と予測したモデルでは、前者のモデルの方がより確信度が高く、好ましい予測と言えるでしょう。交差エントロピーは、このような確信度も考慮に入れた評価を可能にします。さらに、交差エントロピーは、勾配が急になる性質を持っており、学習の初期段階でより早く最適なパラメータへと近づくことができます。これは、シグモイド関数やソフトマックス関数といった活性化関数と組み合わせた際に特に顕著な効果を発揮します。
まとめると、連続値の予測には平均二乗誤差、確率に基づく分類には交差エントロピーを用いるのが適切です。問題の種類に応じて適切な誤差関数を選択することで、モデルの学習効率と性能を向上させることができます。それぞれの誤差関数の特性を理解し、使い分けることが重要です。
| 誤差関数 | 種類 | 説明 | 利点 | 適用 |
|---|---|---|---|---|
| 平均二乗誤差 | 回帰 | 予測値と実測値の差を二乗して平均 | 数値的なずれを捉える | 株価や気温の予測 |
| 交差エントロピー | 分類 | 予測された確率分布全体と真の分布との差を評価 | 確率に基づいた予測の良さを評価、勾配が急で学習が早い | 画像認識(猫、犬など) |
交差エントロピーの最小化

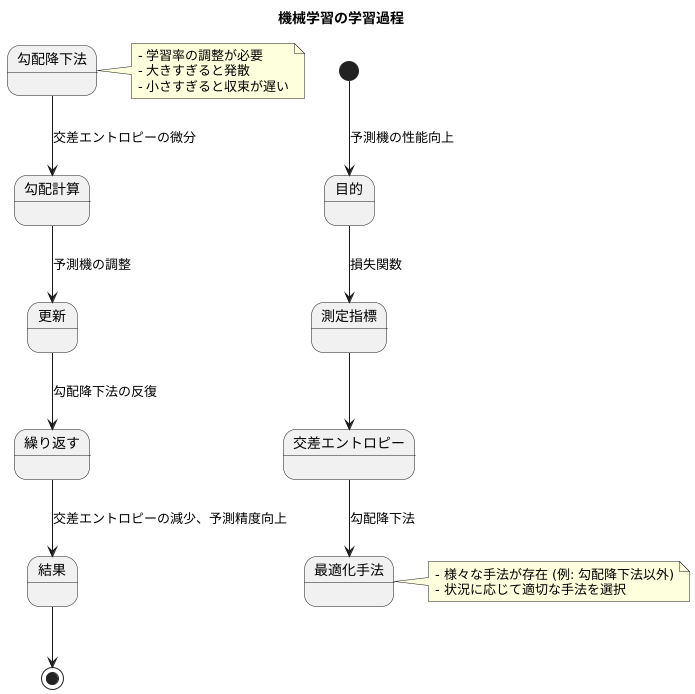
機械学習の目的は、作成した予測機の働きを良くすることです。予測の良し悪しを測る指標として、損失関数と呼ばれるものを使います。損失関数の値が小さいほど、予測機の働きが良いと判断できます。交差エントロピーは、この損失関数としてよく使われる指標の一つです。交差エントロピーを用いる場合、その値を小さくすることで、予測機の性能を高めることができます。
交差エントロピーを小さくするには、勾配降下法といった最適化手法がよく使われます。勾配降下法は、山の斜面を下るように、少しずつ交差エントロピーの値が小さくなる方向を探し出して、予測機を調整する方法です。山の斜面の傾き具合は、交差エントロピーを微分することで計算できます。交差エントロピーは微分できる性質を持っているため、勾配降下法を適用できます。
勾配降下法を何度も繰り返すことで、交差エントロピーは徐々に小さくなり、それに伴って予測機の精度は上がっていきます。まるで、山を下りていくうちに、次第に谷底に近づいていく様子に似ています。しかし、適切な最適化手法を選んだり、学習の速さを調整する値(学習率)を適切に設定したりするなど、交差エントロピーをうまく小さくするには、様々な工夫が必要です。例えば、学習率が大きすぎると、谷底を通り過ぎてしまうかもしれませんし、小さすぎると、なかなか谷底にたどり着かないかもしれません。最適な学習率は、データの性質や予測機の構造によって異なります。また、勾配降下法以外にも、様々な最適化手法が存在し、それぞれに利点と欠点があります。そのため、状況に応じて適切な手法を選択することが重要です。
交差エントロピーのまとめ

機械学習、とりわけ分類問題において、予測の正確さを評価するための重要な尺度として、交差エントロピーと呼ばれるものがあります。これは、真の値と予測値のずれを測る損失関数の一つで、この値が小さいほど、予測が真の値に近いことを示します。
たとえば、画像認識で猫を判別するモデルを考えてみましょう。ある画像が猫である確率をモデルが予測するとします。この時、画像が実際に猫であれば、真の値は猫である確率が1、それ以外の確率は0となります。もし、モデルが猫である確率を0.8と予測した場合、この予測と真の値とのずれを交差エントロピーで計算します。 交差エントロピーの値が小さければ小さいほど、モデルの予測が真の値に近くなり、猫の判別精度が高いことを意味します。
計算方法は、真の値と予測値の対数を用いて行います。具体的な計算式は少し複雑ですが、基本的には真の値が高い事象ほど、予測値とのずれが大きく影響するように設計されています。つまり、猫の画像を犬と誤認識する方が、犬の画像を猫と誤認識するよりも、大きなペナルティが与えられるということです。これは、分類問題において重要な考え方です。
交差エントロピーは、モデルの学習にも利用されます。学習の過程では、モデルのパラメータを調整することで交差エントロピーを最小化しようとします。勾配降下法などの最適化手法を用いることで、徐々にモデルの予測精度を高めていくことができます。 交差エントロピーは微分可能であるため、勾配降下法などの最適化手法を適用しやすいという利点があります。
交差エントロピーを理解することは、機械学習モデル、特に分類モデルを扱う上で非常に重要です。適切な損失関数を選択し、それを最小化することで、高性能なモデルを開発することができます。今後、機械学習を学ぶ上で、交差エントロピーは必ず理解しておくべき重要な概念と言えるでしょう。
| 項目 | 説明 |
|---|---|
| 交差エントロピー | 機械学習の分類問題における損失関数。真の値と予測値のずれを測る。値が小さいほど予測精度が高い。 |
| 役割 | 予測精度の評価、モデル学習における損失関数として利用。 |
| 計算方法 | 真の値と予測値の対数を用いて計算。真の値が高い事象ほど、予測値とのずれの影響が大きい。 |
| 例 | 猫の画像認識:猫である確率を0.8と予測した場合、真の値(猫:1, その他:0)とのずれを交差エントロピーで計算。 |
| モデル学習 | 交差エントロピーを最小化するようにモデルのパラメータを調整(勾配降下法など)。 |
| 利点 | 微分可能であるため、勾配降下法などの最適化手法を適用しやすい。 |
| 重要性 | 機械学習、特に分類モデルを扱う上で非常に重要な概念。 |
