L1正則化:モデルをシンプルにする魔法

AIを知りたい
先生、『L1正則化』って、パラメータを減らして次元圧縮するんですよね?具体的にどういうことですか?

AIエンジニア
そうだね。次元圧縮の効果があるね。L1正則化では、モデルを作る時に、パラメータの絶対値の合計を小さくするように調整するんだ。例えば、たくさんの重みを持つモデルを想像してみて。重みの合計が小さくなるように調整するとどうなるかな?

AIを知りたい
えーと、重みの値が全体的に小さくなるってことですか?

AIエンジニア
そうなんだけど、L1正則化の場合、単に小さくなるだけじゃなくて、不要な重みは0に近づけようとするんだ。結果として、0に近い重みは無視できるようになるから、パラメータの数が減って次元が圧縮されるんだよ。
L1正則化とは。
人工知能で使われる言葉に「L1正則化」というものがあります。これは、作ったモデルが学習しすぎるのを防ぐための一つの方法です。ふつう、正則化では、損失関数と正則化項を足したものをなるべく小さくするようにしますが、L1正則化では、正則化項がパラメータの絶対値の合計で表されます。このため、パラメータの値がゼロになりやすく、結果としてパラメータの数が減ります。これが、次元を圧縮することにつながります。
過学習への対策

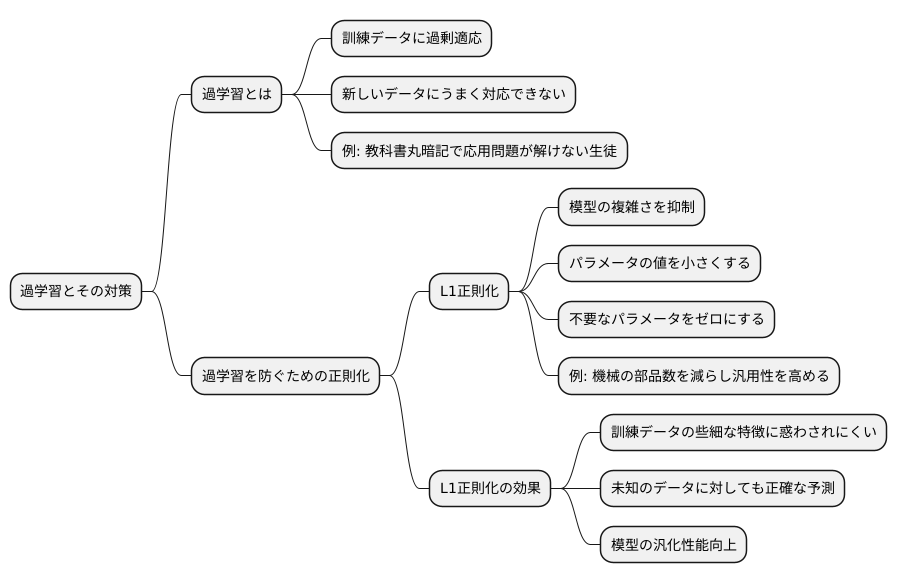
機械学習の模型を作る際には、学習に使った情報に模型が過剰に適応してしまう「過学習」を防ぐことが肝要です。過学習とは、訓練データの細かな特徴や雑音までも学習してしまい、新しいデータに対してうまく対応できなくなる現象です。例えるなら、特定の教科書の内容を丸暗記した生徒は、教科書に載っていない似た問題が出題されると解けなくなる、といった状態です。過学習が起きると、模型は見慣れないデータに対して正確な予測ができなくなり、実用性が損なわれてしまいます。
この過学習を防ぐための有効な手段の一つに「正則化」と呼ばれる技法があります。正則化の中でも、L1正則化は特に強力な手法として知られています。L1正則化は、模型の複雑さを抑えることで過学習を抑制します。模型の複雑さとは、簡単に言えば模型が持つパラメータの多さや、その値の大きさです。L1正則化は、パラメータの値をなるべく小さくするように働きかけ、不要なパラメータを事実上ゼロにすることで、模型を単純化します。
例えるなら、たくさんの部品を組み合わせて複雑な機械を作ったとします。部品が多ければ多いほど、その機械は特定の作業に特化しやすくなりますが、少し違う作業をさせようとすると上手く動作しないかもしれません。L1正則化は、この機械の部品数を減らし、より汎用的な機械にすることに相当します。部品数が減ることで、特定の作業への最適化は弱まりますが、様々な作業に対応できるようになります。
L1正則化によって模型が単純化されると、訓練データの些細な特徴に惑わされにくくなり、結果として未知のデータに対してもより正確な予測ができるようになります。つまり、L1正則化は、模型の汎化性能を高めるための重要な手法と言えるでしょう。
このように、過学習を防ぎ、より汎用性の高い機械学習模型を構築するためには、L1正則化が有効な手段となります。
正則化とは

機械学習において、正則化とはモデルの学習精度を高めるための重要な手法です。学習の目的は、訓練データに含まれるパターンを捉え、未知のデータに対しても正しく予測できるようにすることです。しかし、訓練データに過度に適合してしまうと、未知のデータに対する予測精度が低下する「過学習」という現象が発生します。正則化は、この過学習を防ぐ役割を担っています。
具体的には、正則化はモデルの複雑さを抑えることで実現されます。モデルが複雑すぎると、訓練データの細かなノイズまで学習してしまい、過学習につながります。そこで、モデルのパラメータ(重み)に制約を加えることで、複雑さを調整します。この制約を加えるために、損失関数に正則化項を追加します。損失関数は、モデルの予測値と実際の値との差を表す指標であり、この値を最小化することでモデルの学習が進みます。正則化項は、パラメータの大きさに関するペナルティとして機能します。パラメータの値が大きくなると、正則化項も大きくなり、損失関数全体の値も増加します。そのため、学習過程では、損失関数を最小化するためにパラメータの値が抑制され、結果としてモデルの複雑さが抑えられます。
正則化には、主にL1正則化とL2正則化という二つの手法があります。L1正則化では、正則化項としてパラメータの絶対値の和を用います。この方法では、一部のパラメータがゼロになりやすいという特徴があります。つまり、重要度の低い特徴量に対応するパラメータがゼロになるため、特徴選択の効果も期待できます。一方、L2正則化では、正則化項としてパラメータの二乗和を用います。L1正則化とは異なり、パラメータが完全にゼロになることは稀ですが、全体的にパラメータの値が小さくなるように抑制されます。どちらの手法が適しているかは、データの特性やモデルの構造によって異なります。適切な正則化手法を選択することで、過学習を防ぎ、モデルの汎化性能を高めることが期待できます。
| 正則化手法 | 正則化項 | 特徴 |
|---|---|---|
| L1正則化 | パラメータの絶対値の和 | 一部のパラメータがゼロになりやすい 特徴選択の効果 |
| L2正則化 | パラメータの二乗和 | パラメータが完全にゼロになることは稀 全体的にパラメータの値が小さくなる |
L1正則化の特徴

L1正則化とは、機械学習モデルの学習において、モデルの複雑さを抑える技術の一つです。具体的には、モデルのパラメータの絶対値の合計を損失関数に加えることで、パラメータの値が大きくなりすぎるのを防ぎます。この正則化には、いくつかの特徴があります。
まず、L1正則化はモデルにスパース性をもたらします。つまり、多くのパラメータの値がゼロになります。これは、L1正則化がパラメータをゼロに近づける働きを持つためです。
このスパース性には、いくつかの利点があります。一つ目は、モデルの解釈性が向上することです。ゼロでないパラメータに対応する特徴量のみがモデルの出力に影響を与えるため、どの特徴量が重要なのかが分かりやすくなります。例えば、病気の診断モデルにおいて、数百種類の検査項目の中から、L1正則化によって重要な項目が絞り込まれれば、医師は診断の根拠を理解しやすくなります。
二つ目は、計算コストの削減です。ゼロになったパラメータは計算に不要となるため、計算量やメモリ使用量を削減できます。特に、大規模なデータセットや高次元のデータを取り扱う場合、この効果は大きくなります。膨大なデータを扱う場合、少しでも計算が軽くなれば、処理時間の短縮につながり、より多くの実験や解析が可能になります。
三つ目は、ノイズに対する頑健性の向上です。実世界のデータにはノイズが含まれることが多く、ノイズの影響を受けやすいモデルは、新しいデータに対して正確な予測ができません。L1正則化によって不要な特徴量が排除されると、ノイズの影響を受けにくくなり、未知のデータに対しても安定した予測性能を発揮する、頑健なモデルを構築できます。
このように、L1正則化はモデルをシンプルにし、解釈性を高め、計算コストを削減し、頑健性を向上させることから、様々な機械学習の場面で活用されています。
| 特徴 | 説明 | 利点 | 具体例 |
|---|---|---|---|
| スパース性 (多くのパラメータがゼロになる) |
パラメータの絶対値の合計を損失関数に加えることで、パラメータをゼロに近づける。 |
|
病気の診断モデルで、数百種類の検査項目の中から重要な項目が絞り込まれる。 |
次元圧縮の効果

たくさんの情報を持つデータは、たくさんの軸を持つ座標系で表されることがよくあります。軸が多いほど、データの全体像を捉えるのが難しくなり、たくさんの計算が必要になります。そこで、軸の数を減らし、より少ない軸でデータを表現する方法が次元圧縮です。例えるなら、地図上で建物の高さを色で表現することで、3次元から2次元への次元圧縮を実現できます。
次元圧縮には様々な方法がありますが、その中でL1正則化という方法は、データの特徴を捉える軸の中で、本当に必要な軸だけを残し、不要な軸を消す働きをします。不要な軸に対応する値をゼロにすることで、実質的に軸の数が減り、次元が圧縮されるのです。
このL1正則化による次元圧縮には、幾つかの利点があります。一つ目は、計算の手間が減ることです。軸の数が減れば、計算に使うデータの量も減るため、計算速度が上がり、計算に使う資源も少なくて済みます。また、二つ目の利点として、モデルの精度が向上する場合があることが挙げられます。データの中に紛れ込んだ不要な情報、つまりノイズを減らすことで、本当に重要な情報が際立ち、より正確な予測が可能になるのです。
このように、L1正則化は、高次元データを扱う際に、計算の負担を軽くし、モデルの性能を高めるための強力な手法と言えるでしょう。特に、大量のデータを取り扱う必要がある場合や、データの中にノイズが多い場合に効果を発揮します。軸を減らすことで、データの本質を見抜き、より良い分析結果を得ることができるのです。
| 次元圧縮 | L1正則化 | 利点 |
|---|---|---|
| 高次元データを低次元で表現 | 不要な軸を消すことで次元を圧縮 | 計算の手間を減らす、モデルの精度向上 |
| 例:地図上で建物の高さを色で表現(3次元→2次元) | 不要な軸に対応する値をゼロにする | ノイズを減らし、重要な情報を際立たせる |
他の正則化との比較

色々な種類がある過学習を防ぐ技術の中で、よく知られているものが正則化です。この正則化にも様々な種類があり、それぞれ特徴が異なります。ここでは、代表的な正則化手法であるL1正則化とL2正則化を比較しながら、それぞれの特性を詳しく見ていきましょう。
L1正則化は、正則化項としてモデルのパラメータの絶対値の和を用います。この手法を用いると、多くのパラメータが完全にゼロになり、結果としてモデルが単純になります。このような特性をスパース性と言います。スパース性を持つことで、本当に重要な限られた数の要素だけが残るため、データの解釈が容易になり、不要な情報の削除にも繋がります。つまり、L1正則化は、どの要素が重要かを自動的に選択してくれる、特徴量選択の機能も兼ね備えていると言えるでしょう。
一方、L2正則化は、正則化項としてパラメータの二乗の和を用います。L2正則化もパラメータの値を小さくする効果がありますが、L1正則化のように完全にゼロにすることは稀です。L2正則化は、全てのパラメータを全体的に小さく調整することで、モデルの複雑さを抑え、過学習を防ぎます。L1正則化と比較すると、特定のパラメータを完全にゼロにするスパース性はありませんが、過学習抑制の効果は高く、様々な場面で安定した性能を発揮します。そのため、幅広い問題に対して有効な正則化手法として広く利用されています。
このように、L1正則化とL2正則化は、それぞれ異なる特性を持っています。L1正則化は、モデルを単純化し解釈性を高めたい場合や、特徴量選択を行いたい場合に適しています。一方、L2正則化は、過学習を抑制し、安定した性能を得たい場合に適しています。最終的にどの正則化手法を選択するかは、扱うデータや目的によって異なります。それぞれの特性を理解し、適切に選びましょう。
| 項目 | L1正則化 | L2正則化 |
|---|---|---|
| 正則化項 | パラメータの絶対値の和 | パラメータの二乗の和 |
| パラメータへの影響 | 多くをゼロにする(スパース性) | 全体的に小さくする |
| 効果 | モデルの単純化、特徴量選択 | 過学習抑制 |
| メリット | データの解釈が容易、不要な情報の削除 | 過学習抑制効果が高い、安定した性能 |
| 適した場面 | モデルの解釈性を高めたい場合、特徴量選択を行いたい場合 | 過学習を抑制し、安定した性能を得たい場合 |
実装方法

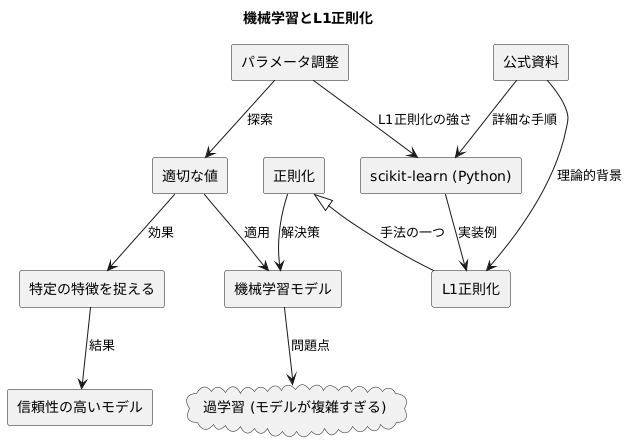
機械学習の手法を使う上で、望ましい結果を得るためには、モデルが複雑になりすぎるのを防ぐ工夫が必要です。そのような工夫の一つに、正則化と呼ばれる手法があります。正則化の中でも、L1正則化はモデルを単純化し、特定の特徴を捉える能力を高める効果があります。
ありがたいことに、多くの機械学習の道具には、L1正則化が簡単に使えるように準備されています。例えば、Pythonでよく使われるscikit-learnという道具には、L1正則化の強さを調整する仕組みが備わっています。この仕組みは、モデルへの影響の度合いを数値で指定できるようになっており、使いやすいのが特徴です。
実際にL1正則化を使うには、この数値を調整しながら、モデルの精度が最も高くなる値を探し出す作業が必要です。適切な値を設定することで、モデルが必要以上に複雑になるのを防ぎ、特定の特徴を的確に捉える能力を高めることができます。結果として、予期せぬデータに惑わされにくい、より信頼性の高いモデルを構築することが可能になります。
L1正則化をscikit-learnで使う具体的な手順は、公式の資料に詳しく書かれています。それぞれの道具の使い方や、正則化の理論的な背景を理解することで、より効果的にL1正則化を活用し、機械学習モデルの性能を向上させることができます。これらの資料は、より深く学ぶための貴重な情報源となります。