L1ノルム損失:機械学習における重要性

AIを知りたい
先生、「L1ノルム損失」ってどういう意味ですか?難しそうでよくわからないです。

AIエンジニア
そうだね、少し難しいかもしれないね。簡単に言うと、機械学習でAIの予測がどれくらい外れているかを測る尺度の一つだよ。 例えば、明日の気温をAIが25度と予測したとして、実際は20度だったら、5度外れていることになるよね。この「外れ具合」を測るのがL1ノルム損失だよ。

AIを知りたい
なるほど。つまり、予測と実際の値の差のことですか?

AIエンジニア
そうだよ。ただし、L1ノルム損失は、差の絶対値の平均を使うんだ。つまり、プラスかマイナスかは気にせず、ただ単にどれくらい離れているかを見るんだね。複数のデータで予測を外した場合、それぞれの外れ具合を足し合わせてデータの数で割ることで平均のずれ具合を求めるんだよ。
L1ノルム損失とは。
人工知能で使われる言葉「L1ノルム損失」について説明します。これは統計学や機械学習の分野で、平均絶対誤差とも呼ばれています。
概要

機械学習では、作った予測モデルが良いか悪いかを数字で測る指標が必要になります。そのような指標の一つに、予測の誤差を測る損失関数というものがあります。その中でも「L1ノルム損失」は、別名「平均絶対誤差」とも呼ばれ、モデルの予測の正確さを評価する重要な指標です。
このL1ノルム損失は、実際の値とモデルが予測した値の差の絶対値を平均したものです。具体的な計算方法は、まず個々のデータ点について、実際の値と予測値の差を計算し、その絶対値を取ります。全てのデータ点についてこの絶対値を合計し、それをデータ点の総数で割ることで、L1ノルム損失が求まります。
L1ノルム損失は、値が小さければ小さいほど、モデルの予測精度が高いことを示します。つまり、損失がゼロに近いほど、モデルの予測は実際の値に近いということです。
L1ノルム損失は、他の損失関数、例えば平均二乗誤差(二乗平均平方根誤差)と比べて、外れ値、つまり予測が大きく外れた値の影響を受けにくいという長所があります。これは、平均二乗誤差は誤差を二乗してから平均するのに対し、L1ノルム損失は誤差の絶対値を平均するためです。二乗すると、大きな誤差はより大きな値となり、平均に大きな影響を与えます。一方、絶対値の場合は、大きな誤差であってもその影響は二乗ほど大きくはなりません。
そのため、もし扱うデータの中にノイズ、つまり本来の値とは異なる異常な値が多く含まれている場合や、予測が大きく外れた値が含まれている場合、L1ノルム損失は平均二乗誤差よりも頑健な指標となります。つまり、ノイズや外れ値に惑わされずに、モデルの本来の性能を適切に評価できます。このような特性から、L1ノルム損失は、特に頑健性が求められるモデルの学習に適しています。
| 損失関数名 | 別名 | 計算方法 | 特徴 | 長所 | 短所 | 適した場面 |
|---|---|---|---|---|---|---|
| L1ノルム損失 | 平均絶対誤差 | 実際の値と予測値の差の絶対値の平均 | 値が小さいほど予測精度が高い | 外れ値の影響を受けにくい | – | ノイズや外れ値が多いデータ |
計算方法

計算方法は、予測と実際の値のずれを測るもので、L1ノルム損失と呼ばれます。この計算は幾つかの手順で行います。
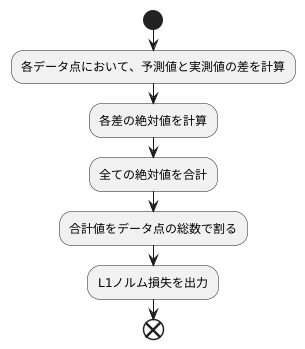
まず、各データ点において、機械学習モデルによる予測値と、実際に観測された値との差を計算します。この差は、予測がどれだけ実測値から離れているかを示すものです。例えば、あるデータ点の予測値が10で、実測値が12だった場合、その差は12引く10で2となります。また、別のデータ点で予測値が5、実測値が3の場合、その差は3引く5でマイナス2となります。
次に、それぞれの差の絶対値を求めます。絶対値とは、その数値の符号を無視した大きさのことです。先ほどの例で、差が2の場合、絶対値は2です。差がマイナス2の場合、絶対値は2となります。つまり、正の数でも負の数でも、絶対値は常に正の数になります。
最後に、これらの絶対値をすべて合計し、データ点の総数で割ります。これは、平均的なずれの大きさを求めるためです。例えば、10個のデータ点があり、それぞれの差の絶対値が1、2、3、4、5、6、7、8、9、10だったとします。これらの値を合計すると55になります。そして、データ点の総数である10で割ると、5.5になります。この5.5が、L1ノルム損失の値です。
まとめると、L1ノルム損失は、各データ点の予測値と実測値の差の絶対値を平均した値です。この値が小さいほど、予測が実測値に近いことを示しています。つまり、L1ノルム損失はモデルの精度を評価する指標の一つとなります。
利点

L1ノルム損失を使うと、いくつも良いことがあります。まず、外れ値、つまり大きく外れた値があってもあまり影響を受けません。平均二乗誤差は誤差を二乗して計算するので、外れた値があると、その二乗が結果に大きく響いてしまいます。しかし、L1ノルム損失は誤差を二乗しないので、大きく外れた値の影響が小さくて済みます。たとえば、たくさんのデータの中にいくつかおかしな値が混じっていても、L1ノルム損失を使えば、それらの値に惑わされずに、しっかりと学習を進めることができます。
もう一つの利点は、まばらなデータ構造を促すことです。まばらなデータ構造とは、たくさんの要素があるデータの中で、値がゼロである要素が多い状態のことを指します。L1ノルム損失を使うと、モデルのパラメータの多くがゼロになりやすい性質があります。これは、モデルをより単純にすることにつながります。モデルが複雑すぎると、学習データに過剰に適応してしまい、新しいデータに対してうまく予測できない「過学習」という状態が起こりやすくなります。パラメータをゼロに近づけることで、モデルを単純化し、過学習を防ぐ効果が期待できます。特に、要素がたくさんある高次元データを扱う場合、この効果は非常に重要になります。
このように、L1ノルム損失は、外れ値に強く、まばらなデータ構造を促すことで過学習を防ぐという利点があります。これらの特徴から、ノイズが多いデータや高次元データの解析に適した損失関数と言えるでしょう。
| L1ノルム損失の利点 | 説明 |
|---|---|
| 外れ値に強い | 誤差を二乗しないため、大きく外れた値の影響が小さい。 |
| まばらなデータ構造を促す | モデルのパラメータの多くがゼロになりやすく、モデルを単純化し過学習を防ぐ。 |
欠点

損失関数の一つであるL1ノルム損失は、頑健性が高いという長所を持つ一方で、いくつかの欠点も抱えています。まず、L1ノルム損失は、ある点で微分ができません。具体的には、誤差がゼロになる点で微分が定義されていません。これは、現在の機械学習で広く使われている勾配降下法などの、勾配に基づいて最適なパラメータを探すアルゴリズムにとって問題となります。勾配が計算できない点があると、アルゴリズムがうまく動作しない可能性があるからです。この問題に対処するためには、微分不可能な点を滑らかに繋ぐ近似的な関数を使うなどの工夫が必要になります。
二つ目の欠点として、L1ノルム損失は最適解が一つとは限らないという点が挙げられます。同じ損失値を与えるモデルが複数存在する可能性があるということです。このような状況では、どのモデルが本当に最適なのかを判断するのが難しくなります。たくさんの適切なモデルの中から最良のモデルを選ぶための基準が必要となるでしょう。
さらに、L1ノルム損失は外れ値に対して強い反面、予測値と真の値の差が小さい場合の調整にはあまり敏感ではありません。つまり、細かな誤差の修正が苦手です。これは、極めて高い精度を求められるタスクにおいては問題となる可能性があります。
しかし、これらの欠点は必ずしも致命的ではありません。適切なアルゴリズムを選んだり、モデルの複雑さを制限する正則化と呼ばれる手法を適用することで、これらの欠点の影響を小さくすることができます。そのため、L1ノルム損失は、欠点を理解した上で適切な対策をとれば、様々な場面で有効な損失関数となり得ます。
| 長所 | 短所 | 対策 |
|---|---|---|
| 頑健性が高い(外れ値に強い) | 微分不可能な点が存在する | 微分不可能な点を滑らかに繋ぐ近似的な関数を使用 |
| 最適解が一つとは限らない | 最適なモデルを選ぶ基準を設定 | |
| 予測値と真の値の差が小さい場合の調整に鈍感 | 正則化手法の適用 |
応用例

L1ノルム損失は、様々な機械学習の課題に役立っています。機械学習では、データから規則性やパターンを見つけることで、未知のデータに対しても予測や判断を行うモデルを作ります。このモデルを作る際に、予測と実際のデータとの誤差を小さくする必要があります。この誤差を測る尺度のひとつが損失関数であり、L1ノルム損失はその一種です。L1ノルム損失は、特に異常値や外れ値と呼ばれる、他のデータから大きく外れた値の影響を抑えたい場合に有効です。通常の二乗誤差を用いる損失関数では、外れ値の影響が大きく出てしまうため、モデルが外れ値に引っ張られてしまい、正しい予測ができなくなる可能性があります。L1ノルム損失を用いることで、外れ値の影響を軽減し、より信頼性の高いモデルを作ることができます。
また、L1ノルム損失は、説明変数のうち、本当に必要な変数だけを選び出す、スパースな解を求めたい場合にも有効です。説明変数とは、予測に用いるデータの特徴を表す変数のことです。多くの説明変数がある場合、全てが予測に役立つわけではなく、むしろモデルを複雑にして予測精度を落とす原因となることもあります。L1ノルム損失を用いると、重要度の低い説明変数の影響をゼロにすることができ、本当に必要な変数だけを選び出した、解釈しやすいシンプルなモデルを作ることができます。これらの特性から、L1ノルム損失は、異常値を含む可能性のあるデータの分析や、多数の特徴量から重要なものだけを選び出す必要があるタスクに適しています。
具体的な応用分野としては、画像のノイズ除去、テキストデータにおける特徴量の選択、頑健な回帰モデルの構築などが挙げられます。画像のノイズ除去では、ノイズを異常値として捉え、L1ノルム損失を用いることでノイズの影響を抑えた画像を復元することができます。テキストデータにおける特徴量の選択では、膨大な単語の中から、文書の分類や感情分析に本当に必要な単語だけを選び出すことができます。金融データ分析のように、外れ値の影響を受けやすいデータの分析にもL1ノルム損失は活用されており、より信頼性の高い予測モデルを構築することができます。このように、L1ノルム損失は様々な分野で活用され、データ分析において重要な役割を担っています。
| L1ノルム損失の特徴 | 効果 | 応用分野 |
|---|---|---|
| 外れ値の影響を抑える | 信頼性の高いモデル作成 | 画像のノイズ除去、金融データ分析 |
| スパースな解を求める(重要な変数を選択) | 解釈しやすいシンプルなモデル作成 | テキストデータにおける特徴量の選択 |
まとめ

機械学習において、学習結果の良し悪しを評価するために損失関数が用いられます。数ある損失関数の中で、L1ノルム損失は特別な位置を占めています。この損失関数は、予測値と真の値の差の絶対値の合計で表されます。一見単純なこの関数が持つ特性は、機械学習モデルの構築に大きな影響を与えます。
L1ノルム損失の大きな特徴の一つは、外れ値に対する頑健性です。つまり、データの中に極端に大きな値や小さな値が含まれていても、それらの値に過度に影響されることなく、安定した学習を行うことができます。これは、二乗誤差を用いるL2ノルム損失と比較すると顕著な違いです。L2ノルム損失は、誤差を二乗するため、外れ値の影響を大きく受けてしまいます。一方、L1ノルム損失は、絶対値を用いるため、外れ値の影響を軽減することができます。
また、L1ノルム損失は、スパース性(疎性)を促進する効果も持ちます。スパース性とは、モデルのパラメータの多くがゼロになる性質を指します。これは、モデルを簡潔にし、解釈性を高める上で重要な役割を果たします。多くの特徴量の中から、本当に重要な特徴量のみを選択する効果があるため、ノイズの多いデータに対しても効果を発揮します。
ただし、L1ノルム損失には、微分不可能な点が存在するという欠点もあります。これは、最適化アルゴリズムによっては、学習が困難になる可能性があることを意味します。しかし、近年の研究により、この微分不可能な点を克服するための様々な手法が開発されています。例えば、微分不可能な点を滑らかに近似する関数を使用する、あるいは、最適化アルゴリズム自体を改良するなど、様々なアプローチがあります。
L1ノルム損失は、様々な応用例でその力を発揮します。特に、頑健なモデルの構築が必要な場合に有効です。例えば、ノイズの多いデータや外れ値を含むデータに対して、安定した性能を発揮するモデルを構築することができます。また、特徴量選択にも効果を発揮するため、高次元のデータ解析においても有用です。L1ノルム損失は、他の損失関数と組み合わせて使用されることもあります。それぞれの損失関数の長所を組み合わせることで、より効果的な学習が可能になります。
データの特性や目的を理解し、適切な損失関数を選択することは、機械学習モデルの構築において非常に重要です。L1ノルム損失はその特性から、特定の状況下において非常に強力なツールとなり得ます。他の損失関数との比較検討を通じて、最適なモデル構築を目指していくことが重要です。
| 項目 | 説明 |
|---|---|
| 定義 | 予測値と真の値の差の絶対値の合計 |
| 特徴 | 外れ値に頑健 |
| スパース性(疎性)を促進 | |
| 欠点 | 微分不可能な点が存在 |
| 対策 | 微分不可能な点を滑らかに近似する関数を使用 |
| 最適化アルゴリズムを改良 | |
| 応用例 | ノイズの多いデータ、外れ値を含むデータへの対応 |
| 特徴量選択 | |
| 高次元のデータ解析 | |
| その他 | 他の損失関数と組み合わせて使用可能 |
