L0正則化:モデルの複雑さを制御する

AIを知りたい
先生、「L0正則化」って、パラメータをなるべくゼロにすることで過学習を防ぐ方法ですよね?でも、なぜ「ゼロの個数」を数える必要があるのでしょうか?普通の正則化と何が違うのですか?

AIエンジニア
良い質問だね。普通の正則化、例えばL1正則化やL2正則化では、パラメータの値を小さくするように働きかけるけど、ゼロにするとは限らない。一方、L0正則化はパラメータがゼロになる個数を直接的に増やすことで、モデルをシンプルにするんだ。

AIを知りたい
なるほど。つまり、本当に必要なパラメータだけを残すということですね。でも、L0正則化は計算が大変だと聞きました。なぜですか?

AIエンジニア
その通り。L0正則化は、パラメータをゼロにするかどうかの組み合わせを全部試す必要があるため、パラメータの数が増えると計算量が爆発的に増えてしまうんだ。だから、実際にはL1正則化などで代用することが多いんだよ。
L0正則化とは。
人工知能で使われる言葉の一つに『L0正則化』というものがあります。これは、学習モデルが、学習データだけに過度に適応してしまい、新しいデータではうまく予測できない状態になることを防ぐ方法の一つです。通常、正則化では、予測の誤差を表す関数と、モデルの複雑さを表す関数の和を最小にするように調整します。L0正則化では、モデルの複雑さを表す関数が、値が0ではないパラメータの数で表されます。つまり、0ではないパラメータが多いほど、モデルが複雑だとみなされます。パラメータとは、モデルの特性を決める値のことです。この方法では、誤差関数に、0ではないパラメータの数を直接加えることになります。しかし、この方法は、どのパラメータが0になるかをあらかじめ予測して最適化する必要があるため、パラメータを少しずつ変化させて最適な値を探す際に使う、微分という計算方法が使えません。そのため、結果として計算量が非常に大きくなってしまうという欠点があります。
正則化とは

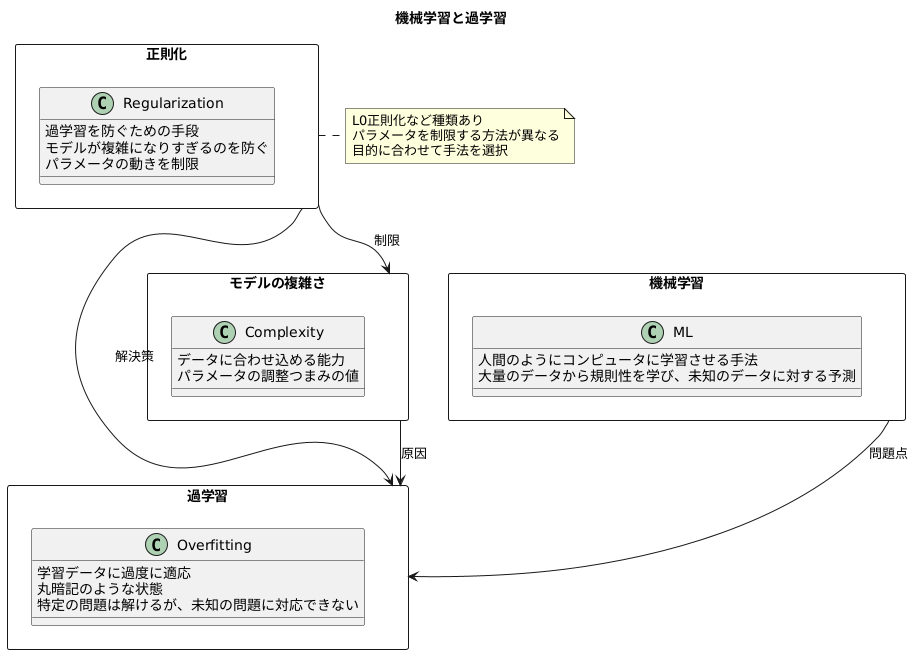
機械学習は、まるで人間のようにコンピュータに学習させる手法です。大量のデータから規則性を学び、未知のデータに対する予測を行います。しかし、学習に使うデータに過度に適応してしまうことがあります。これは、いわば「丸暗記」をしているような状態です。特定の問題は解けるようになっても、少し形を変えた問題や、初めて見る問題には対応できません。これを過学習と呼び、機械学習における大きな課題の一つです。
この過学習を防ぐための有効な手段の一つが正則化です。正則化は、モデルが複雑になりすぎるのを防ぐことで、過学習を抑制します。モデルの複雑さとは、言い換えれば、どれほど細かくデータに合わせ込めるかという能力です。複雑なモデルは、学習データの細かな特徴までも捉えてしまい、結果として過学習を引き起こします。正則化は、モデルの複雑さを抑えることで、学習データの特徴を大まかに捉え、未知のデータにも対応できるようにします。
具体的には、モデルが持つ無数の調整つまみ(パラメータ)の動きを制限することで、複雑さを抑えます。この調整つまみは、モデルが学習データに合わせる際に、細かく調整されます。正則化は、これらのつまみが極端な値にならないように制限をかけるのです。例えば、調整つまみの値が大きくなりすぎると、モデルは学習データの些細な変動にも過剰に反応してしまいます。正則化によってこれらの値を小さく抑えることで、モデルはデータの全体的な傾向を捉え、より滑らかな予測を行うことができるようになります。
正則化には様々な種類があり、それぞれパラメータを制限する方法が異なります。例えば、パラメータの値を0に近づけることでモデルを単純化するL0正則化など、目的に合わせて適切な手法を選択する必要があります。正則化は、機械学習モデルの汎化性能を高めるための重要な手法であり、様々な場面で活用されています。
L0正則化の仕組み

模型を学習させる際、過学習を防ぎ、より質の高い結果を得るために、正則化という手法がよく用いられます。その中でも、L0正則化は、模型の複雑さを効果的に抑えることができる強力な手法です。L0正則化は、模型のパラメータのうち、値が0でないものの個数を数えるという単純な仕組みを持っています。この0でないパラメータの個数が正則化項となり、学習の過程で損失関数に加えられます。
損失関数は、模型の予測値と実際の値との間のずれを表す指標で、この値を最小化することが学習の目標です。ここにL0正則化項が加わることで、単に予測精度を上げるだけでなく、同時に0でないパラメータの数を減らすという目的も加わります。つまり、模型は、限られた数のパラメータだけを使って、できる限り正確に予測を行う必要があるのです。
これは、まるでパズルを解くような作業に似ています。たくさんのピースを使うよりも、必要最小限のピースで完成させる方が、より洗練された美しい解答と言えるでしょう。L0正則化も同様に、本当に必要なパラメータだけを選び出し、無駄を省いた簡潔な模型を作り上げることを目指します。
結果として、L0正則化を用いることで、過学習が抑制され、新しいデータに対してもより正確な予測ができるようになります。さらに、どのパラメータが選ばれたかを見ることで、どの特徴量が重要なのかを理解しやすくなり、模型の解釈性を高めることにも繋がります。また、ノイズのような本質的ではない情報に惑わされにくくなるため、より本質的な特徴を捉えた頑健な模型を構築することが可能になります。
| 正則化手法 | 説明 | メリット |
|---|---|---|
| L0正則化 | 模型のパラメータのうち、値が0でないものの個数を正則化項として損失関数に加える。つまり、使用パラメータ数を制限する。 |
|
計算上の課題

計算上の難しさというものは、物事を数える、あるいは計算する際に直面する困難さを指します。今回のテーマであるエルゼロ正則化も、まさにそのような計算上の難しさに直面する一例です。エルゼロ正則化とは、モデルの複雑さを抑えるための手法で、簡単に言うと、不要な部品をゼロにすることで、モデルを簡素化するものです。
考え方自体は単純で、モデルのパラメータ(部品のようなもの)がゼロになるかどうかの、全ての組み合わせを試せば良いのです。しかし、ここに落とし穴があります。パラメータの数が少し増えただけで、組み合わせの数は爆発的に増えるのです。具体的に言うと、パラメータの数がもし「えぬ」個だとすると、組み合わせの数は2の「えぬ」乗通りにもなります。例えば、パラメータの数が10個でも、1024通り。20個になると、なんと100万通りを超えてしまいます。
このように、パラメータの数が増えるにつれて、組み合わせの数が膨大になり、現実的な時間内で計算を終えることが難しくなります。この難しさを乗り越えるために、様々な工夫が凝らされています。その一つが、エルワン正則化と呼ばれる手法です。エルワン正則化は、エルゼロ正則化の近似計算を行う手法で、パラメータを完全にゼロにするのではなく、ゼロに近づけるという考え方に基づいています。
エルワン正則化では、パラメータの絶対値の合計を小さくするように調整することで、多くのパラメータをゼロに近づける効果があります。この方法は、エルゼロ正則化と比べて計算の手間が大幅に少なく、実用的な時間で計算を終えることができます。そのため、多くの場面でエルワン正則化が選ばれています。エルゼロ正則化は理想的な手法ですが、計算の難しさという壁が立ちはだかります。そこで、計算の負担を軽くしたエルワン正則化が、現実的な解決策として広く利用されているのです。
| 正則化手法 | 説明 | 計算量 | 利点 | 欠点 |
|---|---|---|---|---|
| L0正則化 | モデルのパラメータを0にすることでモデルを簡素化 | パラメータ数nに対して2n通り | 理想的な簡素化 | 計算量が膨大 |
| L1正則化 | L0正則化の近似計算。パラメータを0に近づける | L0正則化より少ない | 実用的な時間で計算可能 | 完全な0にならない |
L1正則化との比較

模型を学習させる際、複雑になりすぎないように調整する手法の一つに正則化があります。正則化には様々な種類があり、その中でよく似た性質を持つL0正則化とL1正則化を比較してみましょう。
どちらも解となる模型のパラメータの多くをゼロに近づけることで、より単純な模型を作ることを目的としています。パラメータがゼロになるということは、そのパラメータに対応する入力データの特徴量が模型の出力に影響を与えないことになるため、結果として単純な模型が得られます。
L0正則化は、ゼロでないパラメータの数を最小化します。つまり、より多くのパラメータを完全にゼロにすることで、最も単純な模型を作ろうとします。この方法は理想的なのですが、ゼロでないパラメータの数を数える処理は数学的に扱いにくく、膨大な計算量が必要になります。そのため、大規模なデータや複雑な模型への適用は現実的ではありません。
一方、L1正則化はパラメータの絶対値の合計を最小化します。L0正則化のようにパラメータを直接ゼロにするわけではありませんが、ゼロに近い値に近づける効果があります。L1正則化は、L0正則化ほど多くのパラメータをゼロにはできませんが、計算が容易です。そのため、大規模なデータや複雑な模型にも適用できます。計算のしやすさと、ある程度の単純さを両立できるため、L1正則化は現実の場面で広く使われています。
さらに、L1正則化にはもう一つ利点があります。それは、微分が可能であることです。微分可能とは、パラメータを少し変化させたときに、模型の出力がどれくらい変化するかを計算できるということです。この性質を利用することで、効率的に最適なパラメータを見つける手法を使うことができます。そのため、L1正則化は実用性の高い正則化手法として選ばれることが多いです。
| 項目 | L0正則化 | L1正則化 |
|---|---|---|
| 目的 | ゼロでないパラメータ数を最小化(最も単純な模型) | パラメータの絶対値の合計を最小化(単純な模型) |
| パラメータ | 多くのパラメータをゼロにする | パラメータをゼロに近い値にする |
| 計算量 | 膨大(非現実的) | 容易 |
| 適用範囲 | 大規模データ・複雑な模型には不向き | 大規模データ・複雑な模型にも適用可能 |
| 微分可能性 | 不可 | 可能 |
| 実用性 | 低い | 高い |
適用事例

この手法は、様々な場面で活用されています。具体的には、特徴量の絞り込みやデータの復元といった課題に有効です。特徴量の絞り込みについて説明します。例えば、病気の診断をするとき、患者の様々な情報(年齢、血圧、体温など)を元に診断を行います。これらの情報を特徴量と呼びます。しかし、全ての情報が診断に役立つわけではありません。中には、診断にあまり関係のない情報も含まれています。そこで、この手法を用いることで、本当に必要な情報だけを選び出すことができます。不要な情報を除外することで、診断の精度を高めるだけでなく、なぜその診断に至ったのかを説明しやすくなります。次に、データの復元について説明します。医療現場での画像診断を例に考えてみましょう。検査装置の性能や時間的な制約から、得られる画像データが不完全な場合があります。この手法は、限られたデータからでも、元の完全な画像を復元するのに役立ちます。少ない情報からでも全体像を把握できるため、検査にかかる時間や費用を削減できます。さらに、信号処理の分野でも活用されています。例えば、音声データからノイズを除去する場合、この手法を用いることで、元の音声信号をより鮮明に復元できます。ノイズに埋もれた重要な情報を抽出できるため、音声認識の精度向上に繋がります。このように、限られた情報からでも効率的に必要な情報を取り出すことができるため、様々な分野で応用され、成果を上げています。特に、データの取得にコストがかかる場合や、データ量が限られている場合に有効です。
| 活用場面 | 課題 | 説明 | メリット |
|---|---|---|---|
| 病気の診断 | 特徴量の絞り込み | 患者の様々な情報(年齢、血圧、体温など)から、診断に本当に必要な情報だけを選び出す。 | 診断の精度向上、診断理由の説明が容易になる |
| 医療現場での画像診断 | データの復元 | 限られた画像データから、元の完全な画像を復元する。 | 検査時間・費用の削減、全体像の把握 |
| 信号処理 | データの復元 | 音声データからノイズを除去し、元の音声信号を鮮明に復元する。 | 音声認識の精度向上 |
今後の展望

今後の展望として、L0正則化技術の進展が期待されます。現状では、L0正則化は計算に多くの資源を必要とするため、計算資源を抑えることができるL1正則化が広く使われています。しかし、L0正則化はL1正則化よりも、より無駄を省いた解を見つけることができるという利点があります。そのため、計算の効率を高めた新しいL0正則化の計算手法の開発が望まれています。もし、計算の手間を減らす方法が見つかれば、L0正則化は幅広い分野で活用されるようになるでしょう。
計算の技術革新もL0正則化の将来を大きく左右します。例えば、量子計算機のような新しい計算技術の発展によって、L0正則化の実用化が進む可能性があります。量子計算機は、従来の計算機では扱うのが難しい複雑な計算を高速で行うことができるため、L0正則化の抱える計算コストの問題を解決する糸口となるかもしれません。
さらに、L0正則化の理論的な性質の解明も重要です。L0正則化は、解に含まれる要素の数を最小にすることで、モデルを簡素化する働きがあります。しかし、その数学的な性質はまだ十分に理解されているとは言えません。L0正則化の理論的な側面をより深く掘り下げることで、計算方法の改良に繋がるだけでなく、今までにない新しい応用分野を発見できる可能性も秘めています。
このように、計算技術の進歩と理論的な研究の進展が相まって、L0正則化は今後ますます重要な役割を担っていくと考えられます。無駄を省きつつ最適な解を見つけるL0正則化は、様々な分野で革新をもたらす可能性を秘めています。
| 展望 | 内容 | 期待される効果 |
|---|---|---|
| L0正則化技術の進展 | 計算資源を抑えるための新しいL0正則化計算手法の開発 | L0正則化の幅広い分野での活用 |
| 計算技術革新 | 量子計算機などの新しい計算技術の発展 | L0正則化の実用化促進 |
| L0正則化の理論的な性質の解明 | L0正則化の数学的な性質の深堀り | 計算方法の改良、新しい応用分野の発見 |
