カーネルトリック:高次元への扉

AIを知りたい
先生、「カーネルトリック」って難しくてよくわからないのですが、もう少し簡単に説明してもらえますか?

AIエンジニア
そうだな。例えば、複雑に曲がった線で分けなければ分類できないデータがあったとしよう。このデータをより高い次元、例えば立体に投影すると、平面で切るだけで分類できるようになる場合がある。この、より高い次元に投影することを考えているんだけども、複雑な計算をせずに済むうまい方法があるんだ。それがカーネルトリックだよ。

AIを知りたい
つまり、高い次元への投影を実際に計算する代わりに、もっと簡単な計算で済ませる方法ということですか?

AIエンジニア
その通り!実際には高次元に変換したかのような結果を、少ない計算量で得られるように工夫した計算方法なんだ。だから「トリック」って言うんだよ。
カーネルトリックとは。
『カーネルトリック』というのは、人工知能の分野でよく使われる言葉です。特に『サポートベクトルマシン』という手法で使われます。サポートベクトルマシンでは、データをより高い次元へ写し変えることで、複雑なデータの分類を簡単にしようとします。しかし、次元を高くすると計算が複雑になってしまいます。そこで、『カーネルトリック』という技法を使って、計算を簡単に済ませるように工夫しているのです。
はじめに

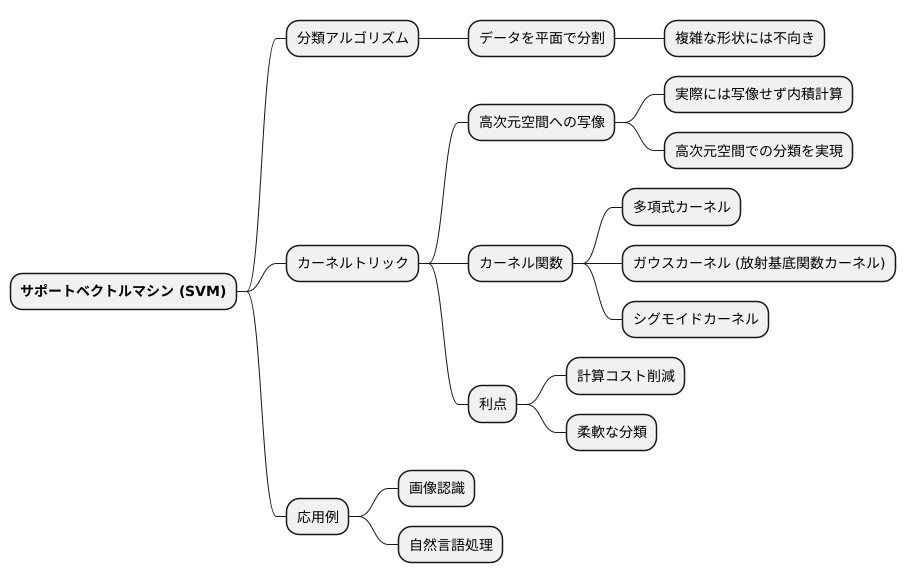
機械学習という分野において、分類のアルゴリズムとしてよく使われているのが、サポートベクトルマシン(略してSVM)です。これは、データの集まりを、最も適した平面によって分割し、分類を行います。しかし、複雑な実際の問題では、単純な直線や平面で分類を行うのは難しい場合があります。例えば、入り組んだ形のデータの集まりをうまく分けることは、直線や平面では不可能です。このような場合に役立つのが、カーネルトリックと呼ばれる手法です。カーネルトリックを使うことで、データをより高い次元の空間に写像し、複雑な分類を可能にします。たとえば、二次元の平面上に散らばるデータを、三次元や四次元といったより高い次元の空間に写像することで、平面では分けられなかったデータも、曲面やより複雑な形状で分類できるようになります。
具体的に説明すると、カーネルトリックは、高次元空間へデータを実際に写像するのではなく、高次元空間におけるデータ同士の「内積」だけを計算します。この計算によって、あたかも高次元空間でデータを扱っているかのような効果を得ることができます。この手法は、「カーネル関数」と呼ばれる特殊な関数を利用することで実現されます。代表的なカーネル関数には、多項式カーネル、ガウスカーネル(放射基底関数カーネル)、シグモイドカーネルなどがあります。それぞれのカーネル関数は異なる特性を持っており、分類したいデータの性質に合わせて適切なカーネル関数を選択することが重要です。例えば、ガウスカーネルは滑らかな曲面でデータを分類するのに適しており、多項式カーネルはより複雑な形状を表現できます。
カーネルトリックの利点は、高次元空間への写像を直接計算する必要がないため、計算コストを削減できる点です。また、様々なカーネル関数を利用することで、データの特性に合わせた柔軟な分類が可能になります。つまり、複雑なデータの分類問題を効率的に解決するための、強力な道具と言えるでしょう。このカーネルトリックによって、SVMは、より複雑な現実世界の問題にも対応できるようになり、画像認識や自然言語処理など、様々な分野で活用されています。
高次元空間への写像

物事を仕分ける際に、二次元平面上に描いた線では分けられない場合があります。例えば、池に浮かぶ丸い葉っぱの周りに、同じく丸く藻が分布している状況を考えてみましょう。葉っぱと藻を分けるには、直線ではなく丸い線が必要です。このような、二次元平面では複雑な仕分けが必要な場合に、高次元空間への写像という考え方が役立ちます。
この考え方を、先ほどの池の例で説明します。池を二次元平面だとすると、葉っぱと藻は二次元平面上に分布しています。ここで、池の水面に高さという新たな次元を加えて三次元空間として捉えてみます。そして、葉っぱのある場所を中心として、水面をドーム状に盛り上げます。すると、元々水面に浮かんでいた藻はドームのふもとに、葉っぱはドームの頂上に位置することになります。この状態で、ドームのふもとと頂上の間を水平に平面で切れば、葉っぱと藻をきれいに分けることができます。これが高次元空間への写像の基本的な考え方です。
この手法の利点は、実際に三次元空間の座標を計算する必要がない点です。カーネル関数と呼ばれる特別な計算方法を用いることで、あたかも三次元空間に写像したかのような効果を得ながら、計算量を大幅に抑えることができます。具体的には、二次元平面上の二点間の距離や角度などの情報から、カーネル関数を用いて、あたかも三次元空間に写像した後の二点間の距離を計算します。この計算結果を用いて、三次元空間で平面を配置し、データの仕分けを行います。このように、カーネル関数を用いることで、高次元空間を扱う複雑な計算を簡略化し、効率的にデータの仕分けを行うことができます。
この高次元空間への写像とカーネル関数を組み合わせた手法は、サポートベクターマシン(SVM)といった機械学習のアルゴリズムで利用されています。SVMは、データの分類や回帰分析などに用いられる強力な手法であり、高次元空間への写像によって、複雑なデータも効率的に扱うことができます。
カーネル関数の役割

カーネル関数は、機械学習、特にサポートベクターマシン(SVM)において重要な役割を担います。SVMは、データ点を分類するための境界線を学習する手法ですが、複雑なデータ構造を持つ場合、線形分離が困難になることがあります。このような場合、データをより高次元の特徴空間に写像することで線形分離を可能にするという方法がとられます。しかし、高次元空間での計算は、計算コストが非常に大きくなってしまうという問題が生じます。
ここでカーネル関数の登場です。カーネル関数は、高次元空間へ実際にデータを写像することなく、その空間での内積を計算することを可能にします。つまり、元のデータ空間での比較的簡単な計算によって、高次元空間での複雑な内積計算を省略できるのです。このおかげで、計算コストを抑えつつ、高次元空間の表現力を活用できます。
代表的なカーネル関数としては、線形カーネル、多項式カーネル、ガウスカーネル(動径基底関数カーネル)などがあります。線形カーネルは、単純な線形分離を行う場合に用いられ、計算が容易という利点があります。多項式カーネルは、データの非線形な関係を捉えることができ、多項式の次数を変えることでモデルの複雑さを調整できます。ガウスカーネルは、非線形分類に特に有効で、複雑なデータ構造にも柔軟に対応できます。ガウスカーネルは、データ点同士の類似度を滑らかに表現できるため、複雑な決定境界を学習できます。
このように、カーネル関数は高次元空間の計算を効率化し、SVMの性能向上に大きく貢献しています。適切なカーネル関数を選択することで、様々なデータ構造に対応した効果的な分類が可能になります。ただし、どのカーネル関数が最適かはデータの特性に依存するため、データに合わせて適切なカーネル関数を選択する必要があります。
| カーネル関数 | 説明 | 利点 | 用途 |
|---|---|---|---|
| 線形カーネル | 単純な線形分離 | 計算が容易 | 線形分離可能なデータ |
| 多項式カーネル | データの非線形な関係を捉える | 多項式の次数でモデルの複雑さを調整可能 | 非線形な関係を持つデータ |
| ガウスカーネル(動径基底関数カーネル) | 非線形分類に特に有効。データ点同士の類似度を滑らかに表現 | 複雑なデータ構造にも柔軟に対応 | 複雑な決定境界が必要なデータ |
計算量の軽減

計算の手間を減らす工夫、それがカーネルトリックです。この手法を使う一番のメリットは、計算量を大幅に減らせることにあります。
たとえば、あるデータを分析する際に、より複雑な特徴を捉えるために、高次元と呼ばれるたくさんの軸を持つ空間にデータを写像することを考えます。このとき、普通に写像を計算しようとすると、軸が増えるほど計算量は爆発的に増えてしまい、とても現実的ではありません。
しかし、カーネルトリックを用いると、この問題を解決できます。カーネル関数という特別な関数を使うことで、高次元空間の具体的な座標を計算する必要がなくなります。つまり、高次元空間へ実際にデータを移すことなく、その空間でのデータの関係性を捉えることができるのです。このおかげで、計算量を大幅に抑えることができるのです。
特に、近年のデータ量の増大に伴い、大規模なデータセットを扱う機会が増えています。このような状況では、計算量の削減は非常に重要です。カーネルトリックは、膨大なデータを扱う際にも効率的に計算を行うことを可能にします。
カーネルトリックは、高次元空間への写像を間接的に行うことで、計算の手間を省きつつ、高次元空間の利点を享受できる、まさに一石二鳥の方法と言えるでしょう。限られた計算資源しかない場合でも、高次元空間での分析を可能にするため、様々な分野で活用されています。まるで、魔法のように計算を簡単にしてくれる、大変便利な手法なのです。
| 項目 | 説明 |
|---|---|
| カーネルトリックの目的 | 計算の手間を減らす |
| メリット | 計算量を大幅に減らせる |
| 高次元空間への写像 | 高次元空間の具体的な座標を計算する必要がない |
| カーネル関数 | 高次元空間へ実際にデータを移すことなく、その空間でのデータの関係性を捉えることができる特別な関数 |
| 効果 | 計算量を大幅に抑える |
| 近年のデータ量の増大 | 大規模なデータセットを扱う際に計算量の削減が重要 |
| カーネルトリックの利点 | 高次元空間への写像を間接的に行うことで、計算の手間を省きつつ、高次元空間の利点を享受できる |
様々な応用

カーネルトリックは、サポートベクターマシン(SVM)以外にも様々な機械学習の場面で活用されています。その応用範囲は広く、高次元データを扱う多くの手法で威力を発揮します。
例えば、カーネル主成分分析を考えてみましょう。主成分分析は、大量のデータに潜む主要な情報を抽出する手法です。高次元データの場合、計算が複雑になりがちですが、カーネルトリックを用いることで、高次元空間を直接扱うことなく効率的に主成分を抽出できます。まるで、複雑な迷路を解くための近道を見つけたかのように、計算の手間を大幅に削減できるのです。
また、カーネルリッジ回帰もカーネルトリックの応用例の一つです。リッジ回帰は、データから予測モデルを作る手法ですが、線形関係しか捉えることができません。しかし、カーネルトリックを導入することで、非線形な関係も捉えられるようになり、より複雑な現象を表現する予測モデルを構築できます。これは、直線ではうまく描けない曲線を、滑らかな曲線で近似するように、予測の精度を高める効果があります。
このように、カーネルトリックは高次元空間を扱うための強力な道具と言えるでしょう。まるで、高次元空間という広大な宇宙を航海するための羅針盤のように、複雑な計算を巧みに誘導し、問題解決を助けます。そして、その応用範囲は、画像認識や自然言語処理、バイオインフォマティクスなど多岐にわたります。膨大なデータが溢れる現代社会において、カーネルトリックの重要性はますます高まっていると言えるでしょう。
| 手法 | 説明 | カーネルトリックの効果 |
|---|---|---|
| カーネル主成分分析 | 大量のデータに潜む主要な情報を抽出する手法。 | 高次元データを直接扱うことなく、効率的に主成分を抽出できる。計算の手間を大幅に削減。 |
| カーネルリッジ回帰 | データから予測モデルを作る手法。 | 非線形な関係も捉えられるようになり、より複雑な現象を表現する予測モデルを構築できる。予測精度を高める効果。 |
まとめ

カーネルトリックとは、機械学習の分野で複雑なデータを扱う際に役立つ、巧妙な計算方法です。この方法は、データを直接高次元空間に写像する代わりに、「カーネル関数」と呼ばれる特殊な関数を用いて、高次元空間での内積を計算します。一見すると回りくどいようですが、実はこの方法を使うことで、高次元空間での計算を効率的に行うことができるのです。
例えば、あるデータが複雑に絡み合っていて、直線では綺麗に分類できないとします。このような場合、データをより多くの情報を含む高次元空間に写像することで、分類が可能になることがあります。しかし、高次元空間での計算は、次元数の増加に伴い、計算量が爆発的に増大するという問題を抱えています。そこで登場するのがカーネルトリックです。カーネルトリックを用いると、実際に高次元空間にデータを写像することなく、高次元空間での内積、つまりデータ間の類似度を計算することができるのです。このため、計算量の爆発を抑えつつ、高次元空間の利点を得ることができるのです。
カーネルトリックは、サポートベクターマシン(SVM)をはじめとする様々な機械学習のアルゴリズムで活用されています。SVMは、データの分類を行うための強力な手法ですが、カーネルトリックを用いることで、より複雑なデータにも対応できるようになります。また、カーネルトリックはSVM以外にも、カーネル主成分分析やカーネルリッジ回帰など、様々な場面で応用されています。このように、カーネルトリックはデータ分析の可能性を広げるための重要な技術と言えるでしょう。今後、データの複雑化が進むにつれて、カーネルトリックの重要性はますます高まっていくと考えられます。カーネルトリックを理解することで、より高度な機械学習モデルの構築が可能になり、複雑なデータに潜む情報をより効果的に活用できるようになるでしょう。
| 項目 | 説明 |
|---|---|
| カーネルトリック | 複雑なデータを扱うための機械学習における計算方法。高次元空間への写像を直接行わず、カーネル関数を用いて高次元空間での内積を計算する。 |
| メリット | 高次元空間での計算を効率化し、計算量の爆発を抑える。 |
| カーネル関数 | 高次元空間での内積を計算するための特殊な関数。 |
| 活用例 | サポートベクターマシン(SVM)、カーネル主成分分析、カーネルリッジ回帰など。 |
| 将来性 | データの複雑化が進むにつれ、重要性はさらに高まる。 |
