カーネル法:高次元への扉

AIを知りたい
先生、カーネルについて教えてください。高次元データを扱うとき、線形分類できない場合に使う手法ですよね?

AIエンジニア
そうだね。簡単に言うと、複雑に絡み合った点をきれいに分類するために、データを別の見方で見て整理するようなものだよ。例えば、平面上に散らばった点を、その平面を曲げることでうまく分類できるようにするイメージだね。

AIを知りたい
平面を曲げる?どういうことでしょうか?

AIエンジニア
例えば、折り紙を想像してみて。平面の折り紙を折ると、立体になるよね。平面では分けられなかった点が、折って立体にすることで簡単に分けられるようになることがある。カーネルは、この『折り方』を決める関数のようなものなんだよ。
カーネルとは。
人工知能でよく使われる「カーネル」という言葉について説明します。カーネルとは、複雑で分類しにくいデータを、より高次元な空間に写し取ることで、分類しやすくする手法のことです。本来は境界線で区切ることが難しいデータも、次元を上げて別の角度から見ることで、線で区切れるようになる場合があります。この写し取る際に使う関数のことを「カーネル関数」といいます。
はじまり

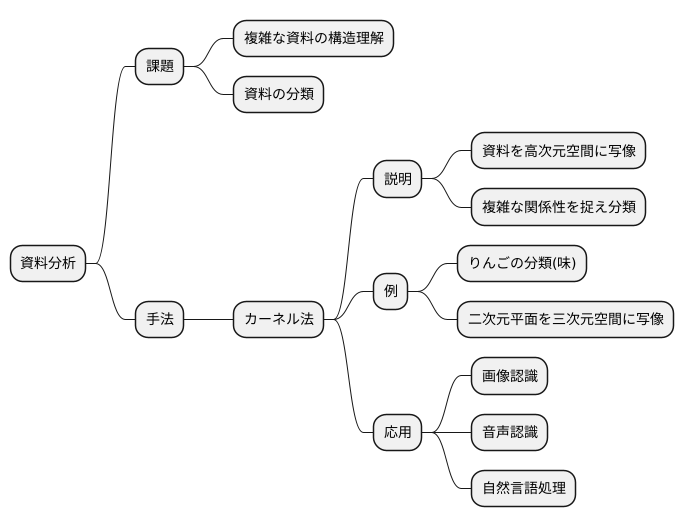
情報の世界で、大量の資料を整理し、意味のある知識を見つけることは、とても大切な仕事です。近年の技術発展に伴い、様々な種類の資料が膨大に蓄積されるようになりましたが、これらの資料は複雑に絡み合い、整理されていないことが多くあります。このような状況で役立つのが、資料分析という手法です。資料分析の中でも、複雑な資料の構造を理解し、分類することは特に重要な課題です。
例えば、りんごの種類を大きさや色で分類することを考えてみましょう。小さな赤いりんご、大きな赤いりんご、小さな緑色のりんごなど、単純な特徴で分類できる場合もあります。しかし、りんごの種類によっては、大きさや色だけでは分類が難しい場合があります。味が似ているりんごを同じ種類として分類したい場合、味という特徴をどのように数値化し、分類に役立てるかは容易ではありません。このような、単純な基準では分類できない資料を扱う際に活躍するのが、カーネル法と呼ばれる手法です。
カーネル法は、資料をより多くの情報が含まれる空間に写像することで、複雑な関係性を捉え、分類を可能にします。例えば、二次元平面上にプロットされた点が直線では分類できない場合、三次元空間に点を写像することで、平面で分類できるようになることがあります。カーネル法は、この写像を巧妙に行うことで、私たちが直接見ることのできない高次元空間での資料の関係性を捉え、分類を可能にします。まるで魔法のように、資料をより高い視点から見て、隠れた関係性を見つけることができるのです。
カーネル法は、資料分析の様々な分野で応用されています。画像認識、音声認識、自然言語処理など、複雑な資料を扱う多くの分野で、その効果を発揮しています。今後、ますます複雑化する資料を扱う上で、カーネル法は重要な役割を担っていくことでしょう。
高次元空間への写像

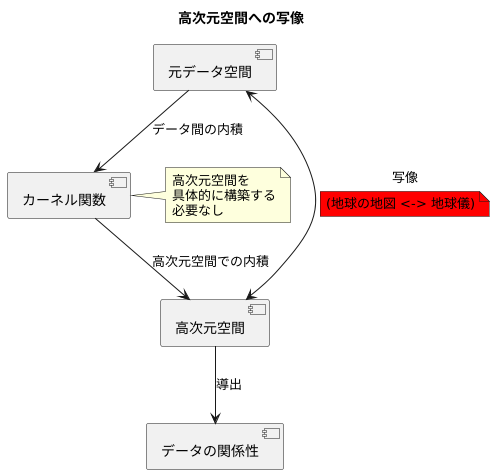
物の見方を広げ、複雑な繋がりを紐解く画期的な方法として、高次元空間への写像という手法があります。この手法は、一見すると難解に思えますが、その核心は意外と単純明快です。例えるなら、平面の地図を立体的な地球儀に投影するように、私たちが普段扱うデータをより多くの情報を取り込める高次元の世界へと変換するのです。
この変換を可能にするのが、カーネル関数と呼ばれる特別な道具です。カーネル関数は、元々のデータ同士の関係性を手がかりに、高次元空間における対応するデータの関係性を導き出します。具体的な手順としては、まず元々のデータ空間で二つのデータ間の内積、つまりデータ同士の類似度のようなものを測ります。そして、カーネル関数はこの値を巧みに変換し、高次元空間での内積として返します。驚くべきことに、この過程で高次元空間そのものを具体的に構築する必要はありません。あたかも、地球儀の実物を作る事なく、平面の地図から地球上の二地点間の距離を計算できるようなものです。
この手法の利点は、計算の手間を大幅に省ける点にあります。高次元空間は、想像を絶するほど複雑で、直接扱うには膨大な計算量が必要になります。しかし、カーネル関数を用いることで、高次元空間そのものを扱うことなく、その空間におけるデータの関係性だけを計算できるのです。つまり、複雑な高次元空間を直接探索することなく、その恩恵だけを効率的に享受できるのです。高次元空間への写像は、データをより深く理解するための、まさに魔法の様な道具と言えるでしょう。
カーネル関数の種類

機械学習において、カーネル関数はデータの類似度を測る重要な役割を担っています。この関数を用いることで、高次元空間へデータを写像し、非線形な関係を持つデータも効果的に分類や分析を行うことができます。カーネル関数は様々な種類があり、それぞれ異なる特性を持っていますので、データの特性や分析の目的に応じて適切なものを選択する必要があります。
代表的なカーネル関数として、まず多項式カーネルが挙げられます。このカーネル関数は、データ間の多項式的な関係性を捉えるのに適しています。例えば、二つのデータの特徴量の積や、それらの高次の積を計算することで、データ間の複雑な関係性を表現することができます。次数を調整することで、モデルの柔軟性を制御することも可能です。
次に、ガウシアンカーネルについて説明します。ガウシアンカーネルは、別名動径基底関数カーネルとも呼ばれ、滑らかで非線形な関係性を捉えるのに優れています。このカーネル関数は、データ間の距離に基づいて類似度を計算します。距離が近いほど値は大きく、遠いほど値は小さくなります。この特性により、データの分布を滑らかに表現し、複雑な分類境界を学習することができます。パラメータを調整することで、滑らかさの程度を制御することも可能です。
最後に、シグモイドカーネルについて説明します。シグモイドカーネルは、ニューラルネットワークの活性化関数であるシグモイド関数と関連性があります。特定のデータ構造に適しており、ニューラルネットワークの学習と似た挙動を示す場合があります。しかし、他のカーネル関数と比べて、必ずしも優れた性能を発揮するとは限りません。
適切なカーネル関数を選ぶことは、機械学習モデルの性能を大きく左右します。多項式カーネルはデータの多項式的な関係性、ガウシアンカーネルは滑らかな非線形関係性、シグモイドカーネルは特定のデータ構造に適しています。データの特性を良く観察し、分析の目的を明確にすることで、最適なカーネル関数を選択し、より精度の高い分析を行うことができます。
| カーネル関数 | 説明 | 特性 | パラメータ |
|---|---|---|---|
| 多項式カーネル | データ間の多項式的な関係性を捉える。 | 特徴量の積や高次の積を計算。モデルの柔軟性が高い。 | 次数 |
| ガウシアンカーネル (RBFカーネル) | 滑らかで非線形な関係性を捉える。データ間の距離に基づいて類似度を計算。 | データの分布を滑らかに表現。複雑な分類境界を学習可能。 | 滑らかさの程度 |
| シグモイドカーネル | ニューラルネットワークの活性化関数であるシグモイド関数と関連性がある。 | 特定のデータ構造に適している。ニューラルネットワークと似た挙動を示す場合も。 | – |
利点

カーネル法には、いくつもの利点があります。まず第一に、高次元空間への写像によって、線形分離不可能なデータも分類できるという点が挙げられます。通常、二次元や三次元といった低次元空間では、複雑に入り組んだデータの境界線を直線や平面でうまく引くことが難しい場合があります。しかし、カーネル法は、データをより高い次元の空間に写像することで、この問題を解決します。高次元空間では、低次元では複雑に見えたデータの構造も、より単純な形で見えるようになり、線形分離が可能になるのです。これにより、複雑なデータ構造を持つ場合でも、カーネル法を用いることで効果的な分類が可能になります。例えば、複雑な曲線でしか分けられないデータも、高次元空間では平面で綺麗に分割できるようになる、といった具合です。
第二に、計算の負担が少ないという利点があります。高次元空間へデータを写像するとはいえ、実際に高次元空間の座標を一つ一つ計算する必要はありません。カーネル関数を用いることで、高次元空間での内積の計算を、もとの空間での計算に置き換えることができるのです。このため、計算量が大幅に削減され、計算にかかる時間やコンピュータ資源を節約できます。これは、特にデータ量が膨大な場合に大きなメリットとなります。膨大なデータを扱う場合、計算コストの増加は大きな問題となりますが、カーネル法を用いることで、この問題を回避し、効率的に分析を進めることができます。
さらに、様々なカーネル関数から、データの特性に適したものを選べるという柔軟性も大きな利点です。カーネル関数は、データ間の類似度を測る尺度のようなもので、様々な種類が提案されています。代表的なものとしては、多項式カーネル、ガウスカーネル、シグモイドカーネルなどがあり、それぞれ異なる特性を持っています。データの分布や特性に応じて適切なカーネル関数を選ぶことで、より精度の高い分析結果を得ることが可能になります。例えば、データの分布が円状になっている場合はガウスカーネル、より複雑な形状の場合は多項式カーネルといったように、データに合わせて最適なカーネル関数を選ぶことで、分析の精度を向上させることができます。
| 利点 | 説明 | 例 |
|---|---|---|
| 高次元空間への写像による線形分離 | 低次元では線形分離不可能なデータも、高次元空間へ写像することで線形分離可能になる。 | 複雑な曲線でしか分けられないデータも、高次元空間では平面で綺麗に分割できる。 |
| 計算の負担が少ない | カーネル関数を用いることで、高次元空間での内積計算をもとの空間での計算に置き換え、計算量を削減。 | 膨大なデータを扱う場合でも、計算コストの増加を回避し、効率的に分析できる。 |
| 柔軟なカーネル選択 | データの特性に適したカーネル関数を選択可能。多項式カーネル、ガウスカーネル、シグモイドカーネルなど、様々な種類がある。 | 円状のデータ分布にはガウスカーネル、複雑な形状には多項式カーネルなど。 |
応用例

カーネル法は、様々な分野の課題解決に役立つ手法であり、実社会で幅広く活用されています。具体的には、画像を扱う分野、言葉を扱う分野、そして生物の情報を扱う分野など、多岐にわたる応用が可能です。
まず、画像を扱う分野では、カーネル法を用いることで画像認識の精度向上が期待できます。写真に写っているものが何なのかを自動的に判断する、画像分類のタスクでは、カーネル法によって画像の特徴を捉えやすくなります。例えば、果物の画像を分類する場合、色や形などの特徴を高次元空間に写像することで、りんご、みかん、バナナといった種類を正確に見分けることが可能になります。また、画像の中から特定の対象物を探し出す物体検出にも、カーネル法は役立ちます。例えば、自動運転技術において、歩行者や信号などを検出する際に、カーネル法を用いることで、周囲の状況をより正確に把握することが可能になります。
次に、言葉を扱う分野では、カーネル法は文章の分析や理解に役立ちます。例えば、文章をテーマごとに分類するタスクでは、カーネル法を用いることで、文章の意味や内容をより深く理解し、適切な分類を行うことが可能になります。ニュース記事を政治、経済、スポーツなどのカテゴリーに分類する作業などがその例です。さらに、文章に込められた感情を読み解く感情分析にもカーネル法は応用できます。商品のレビューに書かれた文章から、顧客が商品に対して肯定的な感情を抱いているのか、否定的な感情を抱いているのかを分析する際に、カーネル法は力を発揮します。
最後に、生物の情報を扱う分野では、カーネル法は遺伝子やたんぱく質の分析に活用されています。膨大な遺伝子データやたんぱく質データから、病気の原因となる遺伝子を見つけ出したり、新薬の開発に役立つ情報を抽出したりする際に、カーネル法は強力なツールとなります。複雑な生命現象を解き明かすためにもカーネル法は重要な役割を担っています。このように、カーネル法は、様々な分野の研究や開発において、データ分析の精度を高め、新たな発見を導き出すための重要な手法となっています。
| 分野 | 応用例 | 詳細 |
|---|---|---|
| 画像 | 画像認識 | 画像分類(例:果物分類)、物体検出(例:自動運転) |
| 画像認識 | 周囲の状況把握 | |
| 言葉 | 文章分析 | 文章分類(例:ニュース記事分類) |
| 感情分析 | 商品レビュー分析 | |
| 生物情報 | 遺伝子/タンパク質分析 | 病気原因遺伝子特定、新薬開発 |
課題と展望

カーネル法は、データ分析において強力な手法として知られていますが、いくつかの課題も抱えています。まず、カーネル関数の選択が分析結果に大きく影響することが挙げられます。カーネル関数は、データ間の類似度を測る尺度であり、分析の目的に適したカーネル関数を選ばなければ、正確な結果を得ることができません。最適なカーネル関数を効率的に選ぶための理論的な枠組みや、経験的な指針は未だ確立されておらず、現在も活発な研究が行われています。
次に、大規模なデータセットへの適用に伴う計算コストの問題があります。カーネル法では、データ数が増加すると計算量が急激に増大する傾向があり、膨大なデータを扱う場合、計算時間が非常に長くなってしまうことがあります。この問題は、カーネル法を様々な分野で広く活用する際の大きな障壁となっています。そのため、計算の負担を軽くし、処理速度を上げるための、より効率的なアルゴリズムの開発が重要な課題となっています。並列計算技術の活用や、近似計算による高速化など、様々なアプローチが試みられています。
これらの課題が解決されれば、カーネル法はさらに多くの分野で応用され、データ分析の可能性を大きく広げることが期待されます。例えば、より複雑なデータ構造を扱うための高度な分析手法の開発や、医療、金融、工学など、様々な分野への応用が考えられます。また、深層学習などの他の機械学習手法との融合による、新たな分析手法の創出も期待されています。カーネル法の持つ可能性を最大限に引き出すためには、これらの課題を克服するための継続的な研究開発が不可欠です。
| 課題 | 詳細 | 対策 |
|---|---|---|
| カーネル関数の選択 | カーネル関数はデータ間の類似度を測る尺度であり、分析の目的に適したカーネル関数を選ばなければ、正確な結果を得ることができません。最適なカーネル関数の選択方法が確立されていない。 | カーネル関数の選択に関する理論的な枠組みや経験的な指針の確立。 |
| 計算コスト | データ数が増加すると計算量が急激に増大し、計算時間が非常に長くなる。 | 効率的なアルゴリズムの開発(並列計算技術の活用、近似計算による高速化など)。 |
