ベクトル自己回帰モデル入門

AIを知りたい
先生、「ベクトル自己回帰モデル」って難しそうでよくわからないです。教えてください。

AIエンジニア
そうですね。「ベクトル自己回帰モデル」は少し難しいですね。簡単に言うと、過去の複数のデータを使って未来の値を予測するモデルです。例えば、気温、湿度、風速など複数のデータから、明日の気温を予測するといった感じです。

AIを知りたい
なるほど。複数のデータを使うところがポイントなんですね。普通の自己回帰モデルとは何が違うんですか?

AIエンジニア
いいところに気がつきましたね。普通の自己回帰モデルは、一つのデータだけを使って予測します。例えば、過去の気温データだけから明日の気温を予測する、といった具合です。ベクトル自己回帰モデルは、複数のデータの関係性も考慮して予測するので、より複雑な現象を捉えることができます。
ベクトル自己回帰モデルとは。
人工知能でよく使われる言葉に「ベクトル自己回帰モデル」というものがあります。これは、過去のデータを使って未来の値を予測する「自己回帰モデル」の一種です。ただ、普通の自己回帰モデルが一つの値を扱うのに対し、ベクトル自己回帰モデルは複数の値をまとめて扱います。たとえば、気温や湿度、風速など、複数のデータが同時に変化していく様子を予測するのに役立ちます。このモデルは、過去の複数のデータがどのように現在の複数のデータに影響を与えているのかを分析し、未来の値を予測します。
自己回帰モデルとは

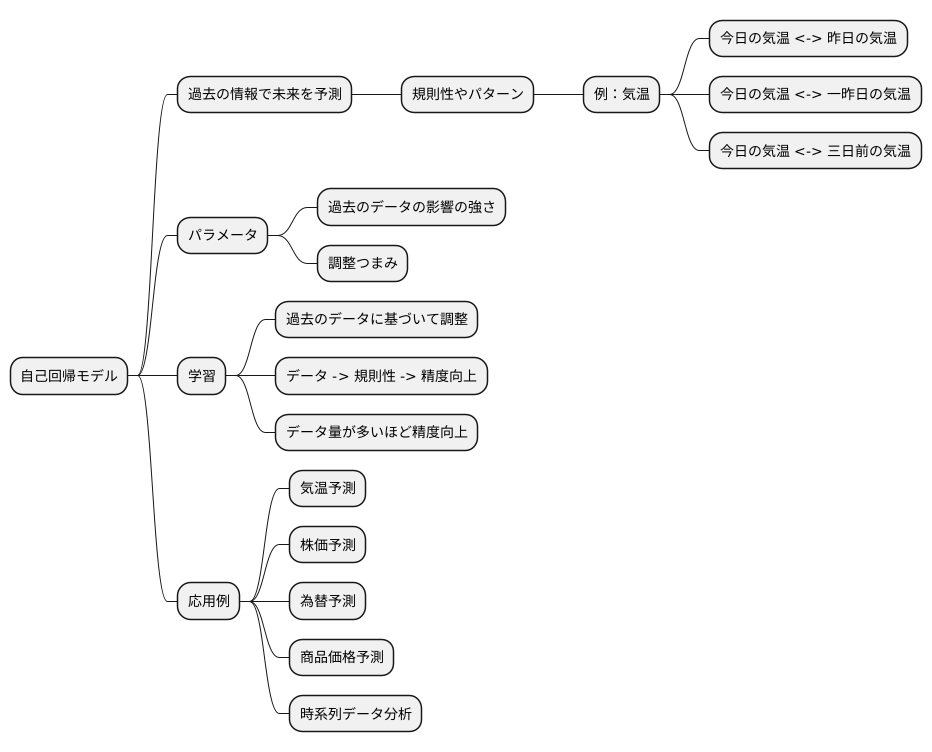
自己回帰モデルは、過去の情報を使って未来を予測するための統計的な手法です。過去のデータの中に潜む規則性や繰り返し現れるパターンを見つけ出すことで、未来の値を推定します。まるで、過去の出来事の足跡をたどって未来への道筋を予想するようなものです。
例えば、毎日の気温の変化を考えてみましょう。今日の気温は、昨日の気温と深い関係があると考えられます。さらに、一昨日の気温も少なからず影響しているかもしれません。三日前の気温の影響は小さいかもしれませんが、全く無いとは言えません。このように、過去のデータが現在の値に影響を与えるという考え方が、自己回帰モデルの基礎となっています。過去のデータの影響の強さは、モデルの調整つまみのような役割を果たす「パラメータ」によって制御されます。
このパラメータは、実際に観測されたデータに基づいて調整されます。過去のデータを使ってモデルを学習させることで、未来の予測精度を高めることができます。学習とは、ちょうど職人が経験を積んで技術を磨くように、モデルがデータから規則性を学び取る過程です。過去のデータが多ければ多いほど、モデルはより多くのことを学び、精度の高い予測が可能になります。
自己回帰モデルは、気温予測だけでなく、株価や為替の動き、商品の値段の変化など、様々な分野で使われています。時間とともに変化するデータ、いわゆる時系列データの分析に特に役立ちます。未来を完全に予測することは難しいですが、過去の情報をうまく活用することで、未来への備えをするための手がかりを得ることができるのです。
ベクトル自己回帰モデルの導入

時系列データを取り扱う際、一つの変数に着目した自己回帰モデルは有用な手法です。しかしながら、現実世界では複数の変数が互いに影響し合うケースが頻繁に見られます。例えば、ある国の経済状況を考えると、経済成長率は金利や為替レート、更には貿易相手国の経済状況にも左右されます。このように複雑に絡み合った複数の変数の関係性を分析するには、従来の自己回帰モデルでは限界があります。そこで、複数の変数の相互作用を捉えるために開発されたのが、ベクトル自己回帰モデル、略してVARモデルです。
VARモデルは、複数の変数の過去の値を用いて、未来の値を予測する統計モデルです。このモデルの核となる考え方は、各変数の過去の値が、他の変数を含む全ての変数の現在値に影響を与えるという仮定です。例えば、過去の金利や為替レート、そして貿易相手国の経済成長率は、現在の経済成長率に影響を与えると考えます。同様に、過去の経済成長率も現在の金利や為替レートに影響を与えると想定します。このように、VARモデルは変数間の相互作用を考慮することで、より現実に近い形で時系列データの分析を可能にします。
VARモデルを使うことで、複数の変数間の複雑な関係性を解き明かすことができます。例えば、金利の変化が経済成長率にどのような影響を与えるのか、あるいは為替レートの変動が貿易収支にどう作用するのかといった分析が可能になります。また、VARモデルは経済予測にも役立ちます。過去のデータに基づいて将来の経済成長率や金利、為替レートなどを予測することで、政策立案や企業の意思決定に有益な情報を提供できます。ただし、VARモデルは変数間の関係性を複雑に捉えるため、モデルの推定や解釈には専門的な知識が必要です。適切なデータの選択やモデルの検証が重要となるため、注意深く取り扱う必要があります。
| モデル | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 自己回帰モデル | 一つの変数の過去の値を用いて、未来の値を予測する統計モデル。 | シンプルで理解しやすい。 | 現実世界の複数変数の相互作用を捉えられない。 |
| ベクトル自己回帰モデル(VARモデル) | 複数の変数の過去の値を用いて、未来の値を予測する統計モデル。各変数の過去の値が、他の変数を含む全ての変数の現在値に影響を与えるという仮定に基づく。 | 複数の変数間の複雑な関係性を解き明かすことができる。経済予測にも役立つ。 | モデルの推定や解釈には専門的な知識が必要。適切なデータの選択やモデルの検証が重要。 |
ベクトル自己回帰モデルの利点

ベクトル自己回帰モデル(VARモデル)には、複数の変数の間の関係性を一度に捉えられるという大きな利点があります。従来よく使われてきた自己回帰モデルは、一つの変数しか扱えませんでした。そのため、経済成長率と金利のように、複数の変数が互いにどう影響し合っているかを調べるのは難しかったのです。例えば、過去の経済成長率から将来の経済成長率を予測できても、金利が経済成長率にどう関係しているかまでは、従来のモデルでは分かりませんでした。
VARモデルでは、複数の変数を同時に扱うことができます。これにより、変数間の複雑な関係性を明らかにすることができます。例えば、経済成長率と金利、為替レートを同時に分析すれば、金利が上がると経済成長率はどう変化するのか、為替レートの変化は経済成長率と金利にどんな影響を与えるのかなど、それぞれの変数が互いにどう作用し合っているのかを詳しく調べることができます。これは、経済の全体像を把握する上で非常に役立ちます。
さらに、VARモデルは将来の値の予測にも役立ちます。従来のモデルでは、一つの変数の過去の値だけを見て将来の値を予測していました。しかし、VARモデルでは、他の変数の過去の値も考慮に入れることができます。例えば、経済成長率を予測する際に、過去の金利や為替レートの情報も利用することで、より正確な予測が可能になります。これは、経済予測だけでなく、金融市場の分析など、様々な分野で役立ちます。将来の株価や債券価格を予測する際にも、複数の関連する指標を同時に考慮することで、より精度の高い予測を行うことができるのです。
| モデル | 変数の数 | 変数間の関係性 | 将来予測 |
|---|---|---|---|
| 従来の自己回帰モデル | 1つ | 捉えられない | 1つの変数の過去の値のみ |
| VARモデル | 複数 | 捉えられる | 複数の変数の過去の値 |
ベクトル自己回帰モデルの適用事例

ベクトル自己回帰モデル、略してVARモデルは、複数の時系列データが互いにどのように影響を与え合っているかを分析する統計的手法です。このモデルは、経済学、金融、販売促進といった様々な分野で活用されており、複雑な関係性を解き明かす強力な道具となっています。
まず、経済学の分野では、国内総生産、物価上昇率、失業率といった主要な経済指標の相互作用を分析するためにVARモデルが用いられています。これらの指標は複雑に絡み合っているため、単独で分析するよりも、VARモデルを用いて複数の指標を同時に分析することで、より正確な経済状況の把握と将来予測が可能になります。例えば、ある経済政策がこれらの指標にどのような影響を与えるかを予測することで、政策の効果を事前に評価することができます。
次に、金融の分野では、株価、金利、為替相場といった金融商品の価格変動を予測するためにVARモデルが利用されます。これらの金融商品は互いに影響を及ぼし合っているため、単独の時系列モデルでは捉えきれない複雑な関係性を分析するためにVARモデルが有効です。例えば、過去のデータに基づいて将来の株価や為替相場の動きを予測することで、投資判断に役立てることができます。
最後に、販売促進の分野では、商品の売上高や広告の効果を分析するためにVARモデルが活用されています。例えば、広告費と売上高の関係性を分析することで、最適な広告戦略を立案することができます。また、競合他社の販売戦略や市場全体の動向といった様々な要因も考慮することで、より効果的な販売促進活動を行うことが可能になります。このように、VARモデルは、複数の時系列データ間の複雑な関係性を分析し、未来を予測するための重要なツールとして、様々な分野で活躍しています。
| 分野 | VARモデルの活用例 | 目的 |
|---|---|---|
| 経済学 | 国内総生産、物価上昇率、失業率といった主要な経済指標の相互作用分析 | 経済状況の把握と将来予測 経済政策の効果評価 |
| 金融 | 株価、金利、為替相場といった金融商品の価格変動予測 | 投資判断の支援 |
| 販売促進 | 商品の売上高や広告の効果分析 競合他社の販売戦略や市場全体の動向分析 |
最適な広告戦略立案 効果的な販売促進活動 |
ベクトル自己回帰モデルの限界

ベクトル自己回帰モデル(VARモデル)は、複数の時系列データ間の相互作用を分析し、将来の値を予測するのに役立つ統計的手法です。しかし、この強力な手法にもいくつかの限界があります。まず、VARモデルは多くの媒介変数を含むため、計算が複雑になることがあります。扱う変数の数が増えるほど、モデルを正確に推定するために必要なデータ量も増大します。十分なデータがない場合、推定された結果は信頼性に欠けるものになる可能性があります。
次に、VARモデルは過去のデータのパターンに基づいて将来の値を予測するため、過去の関係性が未来も変わらないという前提に立っています。しかし、現実の世界は常に変化しています。経済構造の転換や市場環境の変動、政策変更など様々な要因によって、データ間の関係性は変化する可能性があります。そのため、過去のデータに基づく予測が将来も正確であるとは限りません。過去のデータに大きな変化があった場合、モデルの予測精度は低下する可能性があります。
さらに、VARモデルは変数間の因果関係を示すわけではありません。VARモデルは、複数の変数の間の相関関係、つまり変数同士がどのように一緒に変化するのかを分析することはできます。しかし、ある変数の変化が別の変数の変化を引き起こしたのか、あるいはその逆なのか、または両方の変数に影響を与える別の隠れた要因があるのかを判断することはできません。つまり、相関関係と因果関係を混同しないように注意する必要があります。
これらの限界を理解した上で、VARモデルを適切に利用することが重要です。VARモデルは他の分析手法と組み合わせて使用したり、モデルの仮定を慎重に検討することで、より信頼性の高い結果を得ることができます。また、予測結果を鵜呑みにするのではなく、常に現実の状況と照らし合わせて判断することが大切です。
| 限界 | 説明 |
|---|---|
| 計算の複雑さ | 多くの媒介変数を含むため、計算が複雑になり、変数が増えるほど必要なデータ量も増える。データ不足は結果の信頼性低下につながる。 |
| 過去の関係性の持続性の仮定 | 過去のデータに基づいて予測するため、関係性が将来も変わらないと仮定している。しかし、現実の世界は常に変化し、関係性も変化するため、予測精度が低下する可能性がある。 |
| 因果関係の欠如 | 変数間の相関関係は分析できるが、因果関係は示せない。相関関係と因果関係を混同しないように注意が必要。 |
モデルの解釈と注意点

ベクトル自己回帰モデル、略して自己回帰モデルは、複数のデータの関係性を分析し、将来の値を予測するために使われる統計的手法です。しかし、その結果を読み解く際には、いくつかの大切な点に注意しなければなりません。
まず、自己回帰モデルが見せてくれるのは、データ同士の関連性であって、因果関係ではありません。例えば、ある商品の売上高と広告費に関連性が見られたとしても、必ずしも広告費を増やせば売上が増えるとは限りません。他に、景気や天候といった第三の要因が両方に影響を与えている可能性も考えられます。売上高が増えたので広告費を増やしたという、逆の因果関係の可能性もあります。
次に、自己回帰モデルは過去のデータに基づいて将来を予測するものです。ですから、過去のデータの質が予測の精度を大きく左右します。過去のデータに誤りや異常な値が含まれていると、予測の精度は落ちてしまいます。また、経済の仕組みや市場の状況が変化すれば、過去のデータに基づく予測は現実とズレてしまう可能性があります。
さらに、自己回帰モデルは、分析に使うデータの数が多いほど複雑になり、計算に時間がかかります。また、多くのデータを使うと、モデルが複雑になりすぎてしまい、現実の動きをうまく捉えられなくなる「過学習」と呼ばれる状態になる可能性も高くなります。
ですから、自己回帰モデルを使う際には、常に最新のデータを使うとともに、経済状況や市場環境の変化に気を配ることが重要です。また、分析に使うデータの量にも注意を払い、モデルが複雑になりすぎないように工夫することも大切です。これらの点に注意することで、自己回帰モデルをより正しく、効果的に使うことができます。
| 注意点 | 詳細 |
|---|---|
| 相関関係と因果関係 | 自己回帰モデルはデータ間の相関関係を示すものであり、因果関係を証明するものではない。他の要因の影響や逆の因果関係の可能性も考慮する必要がある。 |
| データの質 | 過去のデータの質が予測精度に影響する。誤りや異常値、経済状況や市場の変化は予測のズレにつながる可能性がある。 |
| データ量とモデルの複雑さ | データ量が多いほど計算時間がかかり、過学習のリスクが高まる。適切なデータ量を選択する必要がある。 |
| 最新データと環境変化 | 常に最新のデータを使用し、経済状況や市場環境の変化に注意を払うことが重要。 |
