単純パーセプトロン入門

AIを知りたい
先生、「単純パーセプトロン」って、たくさんの情報を受け取って、一つの答えを出すんですよね?どんなふうに答えを出すのか教えてください。

AIエンジニア
そうだね。たくさんの情報を受け取って、それぞれに重みをかけて足し算するんだよ。そして、その合計がある値を超えたら「1」、超えなかったら「0」といったように、一つの答えを出すんだ。

AIを知りたい
重みをかけるってどういうことですか?

AIエンジニア
それぞれの情報がどれくらい重要かを表す数字だよ。例えば、みかんの値段を決めるのに、大きさの情報には重み「2」、色の情報には重み「1」をかけるとすると、大きさのほうが値段に与える影響が大きいということになるね。
単純パーセプトロンとは。
人工知能の分野でよく使われる言葉に「単純パーセプトロン」というものがあります。これは、たくさんの情報を受け取って、一つの結果を出す、簡単な脳の仕組みをまねた模型のことです。
単純パーセプトロンとは

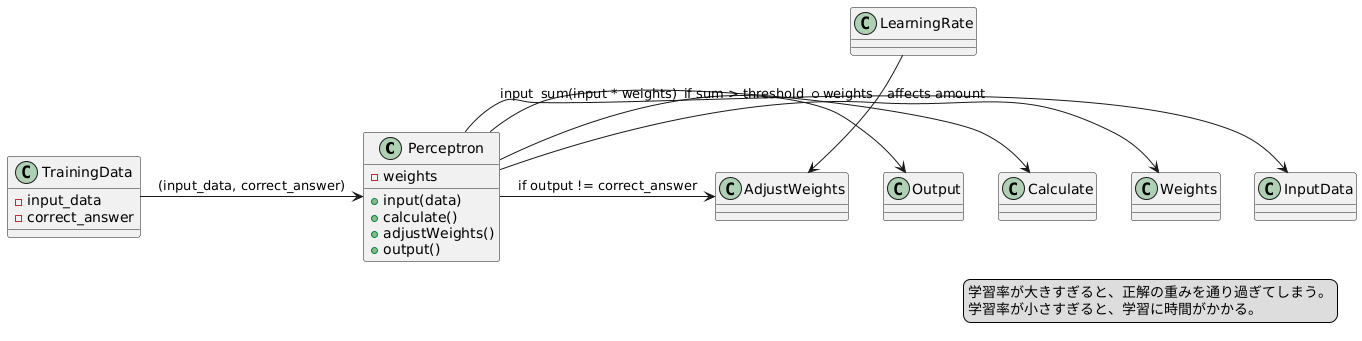
単純パーセプトロンは、人工知能の分野で機械学習の基礎となるものです。これは、人間の脳の神経細胞であるニューロンの働きをまねた模型で、複数の入力信号を受け取り、それぞれの信号に固有の重みを掛け合わせて合計し、その合計値に基づいて出力を生成します。
それぞれの入力信号には、その信号の重要度を表す重みが割り当てられています。これらの重みと入力信号の積をすべて合計し、その合計値がある決められたしきい値を超えた場合、パーセプトロンは1を出力します。逆に、しきい値を超えない場合は0を出力します。これは、生物のニューロンが他のニューロンから信号を受け取り、一定以上の刺激を受けると発火する仕組みに似ています。パーセプトロンは、学習を通じてこれらの重みを調整し、より正確な出力を生成できるように学習していきます。
単純パーセプトロンは、線形分離可能な問題、つまり、直線または平面によって異なる種類に分類できる問題を学習できます。例えば、リンゴとオレンジを大きさや色といった特徴に基づいて分類するといった作業に利用できます。リンゴとオレンジを分類する場合、大きさや色といった特徴が入力信号となり、それぞれの入力信号に対応する重みが設定されます。学習を通じて、これらの重みは調整され、リンゴとオレンジをより正確に分類できるようになります。具体的には、リンゴの特徴に対応する重みは大きく、オレンジの特徴に対応する重みは小さくなるように調整されます。
しかし、単純パーセプトロンは線形分離不可能な問題、つまり、直線または平面で分類できない問題を学習することはできません。例えば、排他的論理和(XOR)のような問題は単純パーセプトロンでは解けません。このような複雑な問題を解くためには、多層パーセプトロンなど、より複雑なネットワーク構造が必要となります。単純パーセプトロンは、線形分離可能な問題を解くための基礎的なモデルであり、より高度な機械学習手法の理解にも役立ちます。
仕組みと学習

単純パーセプトロンは、人の脳神経細胞の働きをまねた、とても簡単なしくみでできています。このしくみは、入力された情報に重みをつけて計算し、その結果がある値を超えたら出力を出す、というものです。この重みを調整することで学習を行います。
はじめは、重みはでたらめに決められます。まるで、生まれたばかりの赤ん坊が何も知らない状態のようです。そして、たくさんの練習問題(訓練データ)を使って、正しい答えを出せるように学習していきます。
訓練データは、入力データと正解の組です。たとえば、りんごの絵を見せて「これはりんごです」と教えるようなものです。パーセプトロンは、入力された情報に現在の重みをかけて計算し、答えを出します。もし、パーセプトロンが「これはみかんです」と間違えたら、重みを調整します。
重みの調整は、正解との違いを縮めるように行います。たとえば、りんごをみかんと間違えた場合、りんごの特徴をより強く、みかんの特徴をより弱くするように重みを調整します。これは、先生がりんごの特徴をもう一度丁寧に教えてくれるようなものです。この調整は、正解との違いが大きいほど大きく、小さいほど小さくなります。
この問題を解いて答え合わせ、重みを調整する、という作業を何度も繰り返すことで、パーセプトロンは訓練データに合った重みを学習していきます。たくさんのりんごやみかんを見て、その特徴を覚えることで、見たことのないりんごやみかんでも正しく見分けられるようになるのです。
重みの調整量を決めるのが学習率と呼ばれるものです。これは、一度にどれくらい重みを調整するかを決める値です。学習率が大きすぎると、正解の重みを通り過ぎてしまうことがあります。逆に小さすぎると、学習に時間がかかってしまいます。ちょうど良い学習率を見つけることが、パーセプトロンを効率よく学習させるために重要です。
適用できる問題

単純パーセプトロンは、主に二つの種類の問題を解くために使われます。一つ目は、分類問題です。分類問題とは、与えられたデータがどのグループに属するかを判断する問題です。例えば、画像を見てそれが猫か犬かを判断する、といった問題です。単純パーセプトロンはこのような問題を、データの持つ特徴を数値化し、それらを重み付けして足し合わせることで解きます。この計算結果がある値を超えると、例えば猫に分類し、そうでなければ犬に分類します。この閾値を境にデータを二つのグループに分類できることから、線形分離可能な問題を解くのに適しています。具体例として、論理回路のANDゲートやORゲートの動作を模倣することができます。ANDゲートは二つの入力が両方とも1の場合のみ1を出力する回路で、ORゲートは少なくともどちらか一方の入力が1の場合に1を出力する回路です。これらの回路の動作は、グラフ上にプロットすると直線で二つの領域に分けられるため、単純パーセプトロンで表現できます。
しかし、単純パーセプトロンでは解けない問題も存在します。例えば、XORゲートは二つの入力が異なる場合のみ1を出力する回路ですが、これはグラフ上で直線で二つの領域に分けることができません。このような線形分離不可能な問題は、単純パーセプトロンでは学習できません。このような問題には、多層パーセプトロンなど、より複雑な仕組みが必要になります。
二つ目は、回帰問題です。回帰問題とは、与えられたデータから連続的な値を予測する問題です。例えば、気温や湿度といったデータから、ある商品の売上げを予測する、といった問題です。単純パーセプトロンは、入力データに重みをつけて足し合わせることで、連続的な値を出力することができます。しかし、単純パーセプトロンは線形の関係しか表現できないため、複雑な曲線で表されるような関係を捉えることは苦手です。そのため、予測の精度が低い場合もあります。より複雑な関係を表現するためには、やはり多層パーセプトロンなど、より高度な手法が必要になります。
| 問題の種類 | 説明 | 例 | 単純パーセプトロンの得意点 | 単純パーセプトロンの苦手点 |
|---|---|---|---|---|
| 分類問題 | データがどのグループに属するかを判断する問題 | 画像の猫/犬分類、論理回路のAND/ORゲート | 線形分離可能な問題を解ける | 線形分離不可能な問題(例: XORゲート)は解けない |
| 回帰問題 | データから連続的な値を予測する問題 | 気温や湿度から商品の売上を予測 | 入力データから連続的な値を出力できる | 複雑な曲線で表される関係は捉えにくい。予測精度が低い場合も。 |
限界と発展

単純パーセプトロンは、データを二つのグループに分ける、いわば仕分け機の役割を果たします。この仕分け作業は、直線で引かれた境界線によって行われます。しかし、この単純な仕組みであるがゆえに、限界も存在します。それは、曲線で区切らなければ分けられない複雑なデータに対応できないということです。例えるなら、リンゴとミカンのように見た目で簡単に区別できるものなら仕分けられますが、様々な種類の果物が混ざっている場合、直線ではうまく仕分けることができません。
この限界を乗り越えるために、多層パーセプトロンという、より高性能な仕組みが開発されました。これは、複数の仕分け機を組み合わせ、複雑な判断を可能にしたものです。それぞれの仕分け機が、異なる特徴に着目してデータを仕分け、その結果を統合することで、曲線で区切られたデータも分類できるようになります。これは、果物の種類だけでなく、大きさや色なども考慮して仕分けするようなものです。
多層パーセプトロンでは、「隠れ層」と呼ばれる中間層が重要な役割を果たします。この隠れ層は、入力されたデータの特徴を段階的に抽出し、より高度な表現に変換する働きをします。隠れ層の数を増やすほど、より複雑な特徴を捉えることができ、より精度の高い分類が可能になります。これは、果物の見分け方をより細かく学習していく過程に似ています。最初は色や形といった単純な特徴で判断していたのが、経験を積むにつれて、香りや触感といったより細かい特徴も見分けられるようになる、というようにです。
さらに、活性化関数という仕組みも、多層パーセプトロンの性能向上に貢献しています。活性化関数は、データの変換処理に、より柔軟性を与えるものです。これにより、直線的な境界線だけでなく、より複雑な曲線を使った境界線も表現できるようになり、複雑なデータにも対応できるようになります。
単純パーセプトロンは、これらの高度な仕組みの基礎となっています。単純パーセプトロンの仕組みを理解することは、複雑なデータ処理の仕組みを理解する第一歩と言えるでしょう。
| 項目 | 単純パーセプトロン | 多層パーセプトロン |
|---|---|---|
| 機能 | データを直線で仕分ける | データを曲線で仕分ける |
| データの種類 | 単純なデータ(例: リンゴとミカン) | 複雑なデータ(例: 様々な種類の果物) |
| 構造 | 単層 | 多層(隠れ層を持つ) |
| 隠れ層 | なし | あり(データの特徴を段階的に抽出) |
| 活性化関数 | なし | あり(複雑な境界線を表現) |
まとめ

単純パーセプトロンは、機械学習の入門として重要な、基本的な学習模型です。複数の信号を受け取り、それらをまとめて一つの信号として出力する仕組みは、人間の脳の神経細胞の働きを模倣しています。それぞれの信号は重み付けされ、その合計値がある値を超えた場合にのみ出力が発生します。これは、まるで神経細胞が発火するかしないかを決定する仕組みのようです。
この単純パーセプトロンは、主に線形分離可能な問題、つまり、直線や平面で綺麗に分類できる問題を解くことができます。例えば、リンゴとミカンを大きさや色で分類するといった問題です。パーセプトロンは、学習を通じて信号の重みを調整することで、分類の精度を向上させていきます。これは、まるで経験を通して物事の判断基準を修正していく人間の学習過程のようです。しかし、単純パーセプトロンには非線形分離可能な問題、つまり、直線や平面で綺麗に分類できない問題には対応できないという限界があります。例えば、ぐちゃぐちゃに混ざった赤と青の点を分類するといった複雑な問題です。このような問題に対しては、単純パーセプトロンでは正確な分類を行うことができません。
この限界を克服するために、多層パーセプトロンといった、より複雑な学習模型が開発されました。多層パーセプトロンは、複数のパーセプトロンを層状に組み合わせることで、より複雑な問題を解くことができます。これは、人間の脳のように、複数の神経細胞が複雑に連携して高度な情報処理を行う仕組みに似ています。単純パーセプトロンは、このような複雑な学習模型の基礎となる重要な概念であり、人工知能の仕組みを学ぶ上で重要な出発点となります。
単純パーセプトロンは、人工知能の発展において歴史的に重要な役割を果たしました。現代の深層学習といった高度な技術も、この単純パーセプトロンの概念を基に発展してきたと言えるでしょう。今後の技術発展のためにも、この基本的な仕組みを理解しておくことは非常に重要です。
