階層的クラスタリング:データの集まりを段階的に

AIを知りたい
先生、『階層的クラスタリング』って、データの集まりを似ているもの同士でまとめていく手法ですよね?どんなふうにまとめていくのか、もう少し詳しく教えてください。

AIエンジニア
そうだね。階層的クラスタリングは、似ているデータ同士を順番にまとめていくことで、グループを階層構造のように作っていく手法だよ。例えば、果物を分類するときに、最初は『りんご』『みかん』『ぶどう』がバラバラにあるとする。まず、似ている『りんご』と『みかん』をまとめて『果物A』というグループにする。それから、『果物A』と少し似ている『ぶどう』をまとめて、さらに大きなグループ『果物B』を作る、といった具合に階層を作っていくんだ。

AIを知りたい
なるほど! 少しずつグループを大きくしていくんですね。でも、どうやってデータが似ているかどうかを判断するんですか?

AIエンジニア
良い質問だね。データが似ているかどうかは、データの特徴を数値で表して、その数値の差が小さいほど似ていると判断するんだ。例えば、果物なら『甘さ』『色』『大きさ』などを数値で表して、それらを比較することで似ているかどうかを判断するんだよ。
階層的クラスタリングとは。
データの集まりを扱う方法の一つに『階層的クラスタリング』というものがあります。これは、似ているデータ同士をまとめてグループを作る方法です。逆に言うと、似ていないデータは別々のグループになるようにします。データをグループにまとめる順番は、似ているもの同士から順に行います。なので、一番似ているデータが最初にグループになり、次に似ているデータがそのグループに加わる、あるいは新しいグループを作る、といったことを繰り返していきます。最終的には、全てのデータが階層構造を持つグループに分けられます。
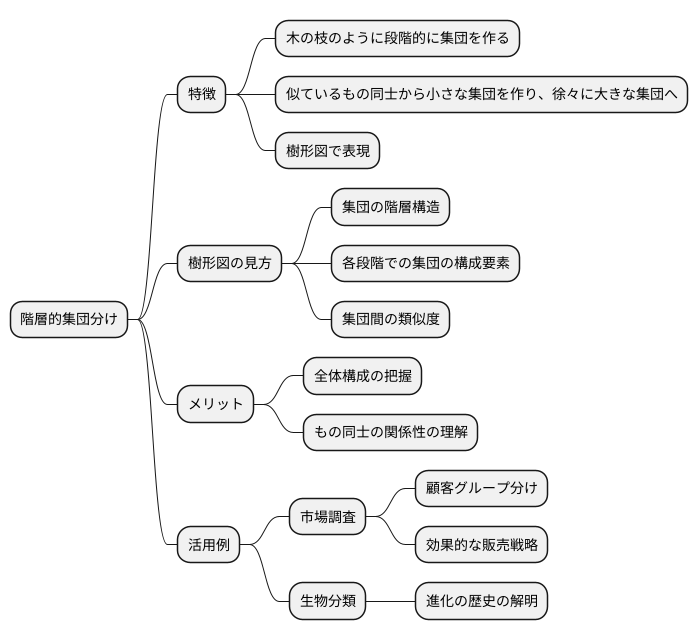
手法の概要

階層的集団分けとは、調べたいものの似ている度合いを手がかりにして、集団を作る方法です。この方法は、まるで木が枝分かれしていくように、段階的に集団を作っていくところが特徴です。似ているもの同士から小さな集団を作り、次にその小さな集団同士をまとめて、より大きな集団を作っていきます。これを繰り返すと、最終的には全てのものが一つの大きな集団にまとまります。
この様子は、まさに木の枝のように広がっていくので、樹形図と呼ばれる図で表現されます。この図を見ると、どのものがどの段階でどの集団に入ったのかが一目で分かります。例えば、ある集団に属するもの同士は、他の集団に属するものよりも似ていると判断できます。また、どの段階でどの集団が合わさったのかも分かります。
この樹形図を見ると、全体がどのように構成されているのか、もの同士の関係がどうなっているのかを掴むのに役立ちます。例えば、市場調査で顧客をグループ分けする場合に、この方法を使うと、顧客の特徴や好みに基づいて似た顧客をまとめることができます。そうすることで、効果的な販売戦略を立てることができます。また、生物の分類を行う際にも、この階層的集団分けは役立ちます。遺伝子の似ている度合いから生物をグループ分けすることで、生物の進化の歴史を解き明かす手がかりとなります。このように、階層的集団分けは様々な分野で活用され、複雑なデータの構造を理解するための強力な道具となっています。
手法の種類

データの集団分けに役立つ階層的クラスタリングには、主に二つの手法があります。一つは、凝集型階層クラスタリングと呼ばれる手法です。この手法は、個々のデータをそれぞれ独立した小さな集団として捉えることから始まります。そして、互いに似通った特徴を持つ集団同士を段階的に結合していきます。最初は、一つ一つバラバラのデータが、まるでそれぞれが小さな島のように存在しています。類似度が高い、つまりよく似た特徴を持つ島同士が橋で結ばれ、徐々に大きな島へと成長していくイメージです。最終的には、全てのデータが一つの巨大な島、すなわち一つの大きな集団へと統合されます。
もう一つは、分割型階層クラスタリングと呼ばれる手法です。こちらは、凝集型とは全く逆のアプローチを取ります。最初は、全てのデータが一つの巨大な集団に属している状態から出発します。この大きな集団を、特徴の違いに基づいて段階的に分割していくのです。まるで、大きな大陸が少しずつ分裂し、最終的にたくさんの島々になるようなイメージです。分割を繰り返すことで、最終的には個々のデータがそれぞれ独立した小さな集団、つまり別々の島々を形成する状態になります。
どちらの手法も、データの中に隠れた階層構造を明らかにすることを目指している点は共通しています。しかし、データのまとめ方、あるいは分割の仕方が異なるため、最終的に出来上がる集団の形や、集団同士の関係性も異なる場合があります。例えるなら、同じ材料を使って家を建てる場合でも、設計図が違えば出来上がる家の形も異なるのと同じです。そのため、分析の目的やデータの特性に合わせて適切な手法を選ぶことが重要となります。
| 手法 | 初期状態 | プロセス | 最終状態 |
|---|---|---|---|
| 凝集型階層クラスタリング | 個々のデータが独立した小さな集団 | 類似した集団同士を段階的に結合 | 全てのデータが一つの大きな集団に統合 |
| 分割型階層クラスタリング | 全てのデータが一つの大きな集団に属する | 大きな集団を段階的に分割 | 個々のデータが独立した小さな集団 |
類似度の尺度

データの集まりを似たもの同士でグループ分けする階層的クラスタリングを行う上で、データ間の似ている度合いを測る尺度の選定は非常に大切です。なぜなら、データの性質や分析の狙いに適した尺度を使わなければ、正しい結果が得られないからです。
数値データの場合、二つのデータ間の距離を測る尺度がよく使われます。例えば、ユークリッド距離は、二つのデータ点を直線で結んだ時の長さを測ります。日常で私たちが距離として認識しているものと同様の考え方です。また、マンハッタン距離は、碁盤の目状の道に沿って進んだ時の距離を測ります。これは、縦と横の移動距離の合計で表されます。これらの尺度は、データの値が数値で表される場合に適しています。
一方、質的データ、例えば色や形など数値で表せないデータの場合は、別の尺度を用います。例えば、ジャカード係数は、二つのデータが共通して持つ属性の数を、全ての属性の数で割ったものです。これは、二つのデータがどれくらい共通点を持っているかを測る尺度です。また、コサイン類似度は、二つのデータのベクトルの間の角度のコサインを計算します。これは、二つのデータの向きの近さを測る尺度です。これらの尺度は、データの値がカテゴリ分けされる場合に適しています。
適切な尺度を選ぶことで、より正確なグループ分けが可能になります。尺度の選定を誤ると、本来似ているデータが異なるグループに分けられたり、逆に似ていないデータが同じグループに分けられたりする可能性があります。そのため、データの性質を理解し、分析の目的に合った尺度を選ぶことが重要です。
| データの種類 | 尺度 | 説明 |
|---|---|---|
| 数値データ | ユークリッド距離 | 二つのデータ点を直線で結んだ時の長さ |
| マンハッタン距離 | 縦と横の移動距離の合計 | |
| 質的データ | ジャカード係数 | 二つのデータが共通して持つ属性の数を、全ての属性の数で割ったもの |
| コサイン類似度 | 二つのデータのベクトルの間の角度のコサイン |
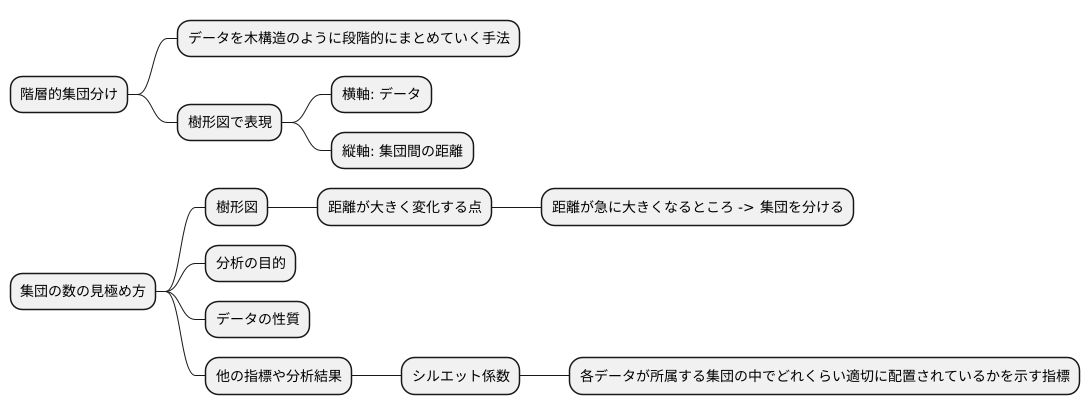
クラスタ数の決定

集団の数を見極めることは、階層的集団分けにおいて重要な課題です。階層的集団分けは、データを木構造のように段階的にまとめていく手法で、その様子を示した図が樹形図です。樹形図は、横軸にデータを、縦軸に集団間の距離を示しています。樹形図をよく見ると、データがどのように集団を形成していくのか、集団同士がどれくらい離れているのかがわかります。
樹形図から集団の数を読み解くには、集団間の距離が大きく変化する点に注目します。距離が急に大きくなるところは、それ以上集団をまとめると性質の異なるものが混ざってしまうことを示唆しています。例えば、樹形図で縦軸の距離が急に伸びている部分があれば、そこを境に集団を分けるのが適切と言えるでしょう。
しかし、集団の数は、分析の目的やデータの性質によって大きく変わるため、樹形図だけを見て判断するのは難しい場合があります。例えば、顧客を年齢層でグループ分けしたい場合と、購買履歴でグループ分けしたい場合では、最適な集団の数は異なります。また、データに含まれる情報の種類や量によっても、適切な集団の数は変わってきます。
樹形図に加えて、他の指標や分析結果も参考にしながら、総合的に判断することが大切です。例えば、シルエット係数などの指標を用いて、各集団内のデータのまとまり具合を評価する方法があります。シルエット係数は、各データが所属する集団の中でどれくらい適切に配置されているかを示す指標です。これらの指標を参考にしながら、データの特性や分析の目的に合った集団の数を見つける必要があります。闇雲に集団を多くしたり少なくしたりするのではなく、様々な情報を組み合わせて慎重に判断することが重要です。
応用例

階層的集団分けは、様々な分野で活用されている、データ分析の有力な手法です。階層構造を持つ樹形図によって、データの集団間の関連性を視覚的に把握することができます。この手法は、データの類似度に基づいて集団を段階的に結合または分割していくことで、複雑なデータ構造を分かりやすく表現します。
例えば、販売戦略においては、顧客をいくつかの集団に分類するために利用されます。顧客の購入履歴や属性データに基づいて集団分けを行うことで、それぞれの集団に適した販売促進計画を立てることが可能になります。例えば、過去の購入商品、ウェブサイトの閲覧履歴、年齢、性別といったデータを用いて顧客を階層的に分類することで、各集団に合わせたおすすめ商品表示やクーポン配布といった、より効果的な販売戦略を実現することができます。
生物学の分野でも、生物の分類に活用されています。生物の遺伝子情報や形態データに基づいて集団分けを行うことで、生物の進化の過程や種間の関係性を明らかにすることができます。例えば、様々な生物種の遺伝子配列を比較し、階層的集団分けを用いることで、系統樹を作成し、生物の進化の歴史を解明することができます。
情報科学の分野では、文書の分類に利用されます。大量の文書データを、内容の類似度に基づいて自動的に分類することで、情報の整理や検索効率の向上に役立ちます。例えば、ニュース記事を階層的集団分けによって分類することで、関連性の高い記事をまとめて表示したり、特定の話題に関する記事を効率的に検索したりすることができます。このように、階層的集団分けは、データの構造や関係性を理解するための強力な手法として、幅広い分野で役立てられています。
| 分野 | 活用例 | データ例 | 利点 |
|---|---|---|---|
| 販売戦略 | 顧客の分類 | 購入履歴、ウェブサイト閲覧履歴、年齢、性別 | 効果的な販売促進計画(おすすめ商品表示、クーポン配布など) |
| 生物学 | 生物の分類 | 遺伝子情報、形態データ | 進化過程や種間関係性の解明(系統樹作成) |
| 情報科学 | 文書の分類 | 文書データ | 情報の整理、検索効率向上(関連記事表示、効率的検索) |
長所と短所

階層的クラスタリングは、データの構造を木構造のように視覚化できるという利点があります。この木構造の図をデンドログラムと呼びます。デンドログラムを見れば、どのデータがどの段階で仲間としてまとめられたのかが一目瞭然です。まるで家系図のように、データの関係性を掴むことができ、データの背後にある隠れた構造を理解するのに役立ちます。
また、階層的クラスタリングを使う際に、あらかじめ仲間の数を決めておく必要はありません。他の手法では、データをいくつの仲間に分けるかを最初に決める必要がありますが、階層的クラスタリングはデータの繋がり具合を見ながら、柔軟に仲間分けを進めていくことができます。そのため、データの性質に合わせて、最適な仲間分けを見つけることが可能です。
しかし、階層的クラスタリングには計算に時間がかかるという欠点もあります。扱うデータの量が多いほど、計算量は増大し、結果を得るまでに長い時間がかかってしまうことがあります。特に、莫大なデータを扱う場合は、現実的な時間内で計算を終えることが難しい場合もあります。ですので、大規模なデータ分析には不向きです。
さらに、雑音や異常値に影響されやすいという点も課題です。データの中に紛れ込んだ不正な値や本来とは異なる値があると、仲間分けの結果が大きく変わってしまう可能性があります。そのため、階層的クラスタリングを行う前に、データの質をよく確認し、必要に応じて前処理を行うことが重要です。前処理では、雑音を取り除いたり、異常値を修正したりすることで、より正確な結果を得られるようにデータの下準備を行います。
このように、階層的クラスタリングはメリットとデメリットを併せ持っています。データの特性や分析の目的を理解し、適切な方法で利用することで、データ分析における強力な手法となります。
| 項目 | 説明 |
|---|---|
| メリット |
|
| デメリット |
|
| その他 |
|
