群平均法:データの塊を比べる賢い方法

AIを知りたい
先生、「群平均法」って、たくさんのデータが集まった塊を比べる方法ですよね?よくわからないので教えてください。

AIエンジニア
そうだね。「群平均法」は、データの塊り、つまりクラスタを比べる方法の一つだ。それぞれのクラスタに属するデータ同士を全て比べ、その距離の平均をクラスタ間の距離とするんだよ。

AIを知りたい
全てのデータ同士を比べるんですか?大変そうですね。具体的にどういう利点があるのでしょうか?

AIエンジニア
確かに計算量は多いね。しかし、クラスタの中に極端に離れた値のデータ、いわゆる外れ値があっても、全体の平均なので、結果に大きな影響を与えにくいという利点があるんだ。
群平均法とは。
二つの集団を作るデータについて、その集団同士の関係性を測る方法の一つに『群平均法』というものがあります。この方法は、それぞれの集団に属するデータの全ての組み合わせについて、データ同士の距離を計算し、その平均値を集団間の距離とします。全ての組み合わせの距離の平均を使うので、集団の中に極端に離れた値を持つデータがあったとしても、結果に大きな影響が出にくいという特徴があります。
データの塊を比べる方法

多くの情報が集まった大きなデータから、役に立つ知識を見つけるためには、データをいくつかの集まりに分けて、それぞれの集まりの特徴をつかむことが大切です。このようなデータの集まりを「かたまり」と呼ぶことにします。しかし、かたまり同士をどのように比べれば良いのでしょうか?かたまり同士を比べる一つの方法として、「集まり全体を平均した値で比べる方法」があります。この方法は、それぞれの集まりに属するデータの平均値を計算し、その平均値同士の差を見ることで、集まり同士の似ている度合いを測ります。
たとえば、ある商品の購入者のデータを考えてみましょう。購入者の年齢、性別、購入金額など、様々な情報が集まったデータがあるとします。このデータをいくつかの「かたまり」に分けて、それぞれの「かたまり」の特徴を調べたいとします。
まず、年齢のかたまりで考えてみます。20代、30代、40代といった年齢層にデータを分けて、それぞれの年齢層の平均購入金額を計算します。20代の平均購入金額が1万円、30代の平均購入金額が2万円、40代の平均購入金額が3万円だとします。この結果から、年齢層が高くなるにつれて購入金額も高くなる傾向があるとわかります。
次に、性別の「かたまり」で考えてみます。男性と女性にデータを分けて、それぞれの性別の平均購入金額を計算します。男性の平均購入金額が2万円、女性の平均購入金額が1.5万円だとします。この結果から、男性の方が女性よりも購入金額が高い傾向があるとわかります。このように、「集まり全体を平均した値で比べる方法」を使うことで、異なる「かたまり」の特徴を比較し、データ全体をより深く理解することができます。もちろん、平均値だけで比べるのではなく、他の情報も合わせて考えることが大切です。たとえば、それぞれの「かたまり」に含まれるデータの数や、データのばらつき具合なども考慮することで、より正確な分析ができます。
さらに、「集まり全体を平均した値で比べる方法」は、商品の売上予測や顧客の分類など、様々な場面で活用できます。適切なデータ分析を行うことで、ビジネス戦略の改善や新商品の開発など、様々な分野で役立てることができるのです。
| 集まりの種類 | 集まりの分け方 | 平均値の比較結果 | 得られる傾向 |
|---|---|---|---|
| 年齢 | 20代、30代、40代 | 20代: 1万円、30代: 2万円、40代: 3万円 | 年齢層が高くなるにつれて購入金額も高くなる |
| 性別 | 男性、女性 | 男性: 2万円、女性: 1.5万円 | 男性の方が女性よりも購入金額が高い |
群平均法の仕組み

群平均法は、データの集まりをいくつかの塊に分けて比べる方法です。複数のデータの集まりを比べる際に、それぞれの集まりを代表する値だけを比べるのではなく、集まりに含まれる全てのデータ同士の関係性を考慮することで、より詳しい比較を行うことができます。この手法は、特にデータのばらつきが大きい場合や、集まりごとのデータ数が異なる場合に有効です。
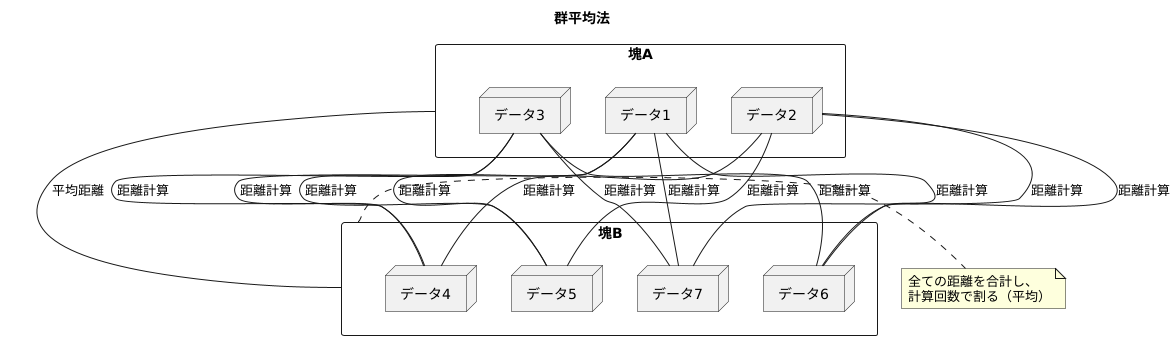
具体的には、まず比べる対象となる二つの塊を考えます。それぞれの塊には、複数のデータが含まれています。群平均法では、片方の塊に含まれる全てのデータと、もう片方の塊に含まれる全てのデータとの間の距離を、一つずつ全て計算します。例えば、仮に最初の塊に3つのデータ、もう一つの塊に4つのデータがあるとします。すると、3つのデータそれぞれと、4つのデータそれぞれの間の距離を計算するため、全部で3かける4で12通りの計算が必要になります。
全ての組み合わせの距離を計算したら、それらを全て足し合わせ、計算した回数で割ります。つまり、平均値を求めます。この平均値が、二つの塊の間の距離として扱われます。個々のデータ同士の距離を見るのではなく、全ての組み合わせの平均値を用いることで、塊全体の傾向を捉え、外れ値のような一部の極端なデータの影響を受けにくく、安定した比較が可能になります。また、それぞれの塊に含まれるデータの数が異なっていても、全てのデータ間の距離を考慮することで、公平な比較ができます。
このように、群平均法は、塊に含まれる全てのデータ間の距離を平均することで、塊間の距離を測る方法です。この方法を用いることで、より正確で、データのばらつきに強い比較を行うことができます。
外れ値に強い

集団の平均を用いる方法は、極端な値に左右されにくいという利点があります。時折、集めたデータの中に、他のデータから大きく外れた値が混じる場合があります。このような値を外れ値と呼びます。例えば、多くの生徒の試験の点が50点から70点の間に集中しているのに、一人だけ10点だった場合、この10点が外れ値に該当します。もし、このような外れ値をそのまま分析に含めてしまうと、結果が大きく歪んでしまうことがあります。例えば、全体の平均点を計算すると、外れ値によって平均点が本来よりも低く出てしまうでしょう。しかし、集団の平均を用いる方法では、全てのデータの組み合わせについて距離を計算し、その平均を求めます。つまり、一つの極端な値の影響が薄められ、全体の結果に大きな影響を与えなくなります。これは、多数の組み合わせの中で、外れ値を含む組み合わせは一部に過ぎないためです。現実のデータには、測定誤差や予期せぬ出来事などによるノイズが混入することがよくあります。このようなノイズは外れ値として現れることが多いため、ノイズに強い分析手法は実用上非常に重要です。集団の平均を用いる方法は、このようなノイズを含むデータでも安定した結果を得られるため、信頼性の高い分析が可能になります。例えば、工場で製造される製品の品質検査を行う場合、一部の製品に欠陥があったとしても、集団の平均を用いる方法であれば、全体の品質傾向を正しく把握できます。また、都市の気温変化を分析する場合、ある日に突発的な異常気象があったとしても、長期的な気温の傾向を正確に捉えることができます。このように、集団の平均を用いる方法は、様々な分野で正確な分析を行うための強力な道具となります。
| 方法 | 利点 | 外れ値の影響 | ノイズの影響 | 適用例 |
|---|---|---|---|---|
| 集団の平均を用いる方法 | 極端な値に左右されにくい | 影響が薄められる | 安定した結果を得られる | 製品の品質検査、都市の気温変化分析 |
計算の手間

集団の平均を用いる方法は、データ一つ一つを他の全てのデータと比べ、その間隔を測る必要があるため、データの数が膨大な際は計算に多くの時間がかかります。特に、扱うデータの規模が非常に大きい場合、計算にかかる時間や資源を慎重に考える必要があります。例えば、一万個のデータがあれば、組み合わせはほぼ五千万通りにもなり、単純計算でも莫大な回数の間隔計算が必要となります。もしこの計算に一つにつき0.001秒かかるとすれば、全体で5000秒、つまり約1時間半もの時間がかかってしまうことになります。データが更に増えれば、計算時間は飛躍的に増加し、数日、数週間かかる場合も考えられます。これは、研究や実務において大きな支障となる可能性があります。
しかし、近年の計算機の処理能力の向上は目覚ましく、以前と比較すると計算速度は大幅に速くなっています。並列処理技術や専用計算機の登場により、膨大なデータの処理も現実的な時間で行えるようになってきています。例えば、以前は数日かかっていた計算が数時間で終わったり、数時間かかっていた計算が数分で終わるといったことも珍しくありません。また、計算アルゴリズムの改良も進み、計算の効率化が図られています。例えば、近似計算を用いることで、計算の精度を少し落とす代わりに計算時間を大幅に短縮する手法なども開発されています。
これらの技術革新により、多くの状況において、集団の平均を用いる方法は実用的な時間内で計算を完了することが可能になっています。ただし、データの規模や計算機の性能によっては、依然として計算時間が問題となるケースも存在します。そのため、巨大なデータを扱う際は、計算時間を見積もり、適切な計算資源を用意することが重要です。また、計算アルゴリズムの選択や並列処理の活用など、計算の効率化を図る工夫も必要に応じて検討するべきでしょう。
| 項目 | 説明 |
|---|---|
| 集団の平均を用いる方法の課題 | データ数が多い場合、計算時間が膨大になる。1万個のデータで約1時間半かかる場合も。 |
| 計算機の進化 | 並列処理、専用計算機、アルゴリズム改良により計算速度が大幅に向上。 |
| 現状と対策 | 多くの場合、実用的な時間で計算可能。ただし、巨大データの場合は計算時間を見積もり、適切な資源を用意。アルゴリズム選択や並列処理も検討。 |
他の方法との比較

データの集まりをいくつかの塊に分ける方法を考える時、塊同士がどれくらい離れているかを測ることはとても大切です。この距離の測り方には、色々なやり方があります。よく使われる「群平均法」以外にも、幾つかの方法がありますので、ここで詳しく見ていきましょう。
例えば、「塊の中心同士の距離を測る方法」があります。それぞれの塊で、データの位置の平均値を計算し、その平均値同士の距離を測ることで、塊同士の距離とします。この方法は、計算が比較的簡単なので、手軽に距離を測りたい時に便利です。しかし、それぞれの塊の中に極端に離れた値を持つデータ(外れ値)があると、その影響を受けやすく、正確な距離が測れないことがあります。
次に、「最も近いデータ同士の距離を測る方法」を見てみましょう。二つの塊それぞれから、一番距離が近いデータを選び、その二つのデータ間の距離を塊間の距離とします。この方法は、計算が非常に速いという利点があります。しかし、外れ値があるとその値に大きく左右されてしまいやすいという欠点も持ち合わせています。全体的な傾向を捉えるのが難しくなることもあります。
これらに対して、「群平均法」は、全てのデータ間の距離を計算し、その平均値を用いる方法です。そのため、特定のデータに過度に影響されることが少なく、安定した結果を得やすいという特徴があります。しかし、全てのデータ間の距離を計算する必要があるため、他の方法に比べて計算に時間がかかるというデメリットもあります。
このように、それぞれの距離の測り方には、良い点と悪い点があります。データの性質や分析の目的を考えながら、どの方法が最適かを判断する必要があります。もし、データの中に外れ値が含まれている可能性が高く、より正確に塊間の距離を測りたい場合は、群平均法が適しているでしょう。一方で、データ数が非常に多く、計算時間を短縮したい場合は、中心同士の距離を測る、あるいは最も近いデータ間の距離を測る方法が適しているかもしれません。色々な方法を比較検討し、状況に応じて最適な方法を選ぶことが重要です。
| 方法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 塊の中心同士の距離を測る方法 | 各塊のデータの平均値同士の距離を測る | 計算が簡単 | 外れ値の影響を受けやすい |
| 最も近いデータ同士の距離を測る方法 | 二つの塊から最も近いデータを選び、そのデータ間の距離を測る | 計算が速い | 外れ値に大きく左右されやすい、全体的な傾向を捉えにくい |
| 群平均法 | 全てのデータ間の距離の平均値を用いる | 外れ値の影響を受けにくい、安定した結果 | 計算に時間がかかる |
まとめ

複数の集団の平均値を比べる方法、群平均法についてまとめます。この方法は、集団全体の平均値を計算し、それらを比較することで集団間の違いを明らかにするものです。
群平均法の大きな利点は、外れ値の影響を受けにくいことです。 個々のデータが大きく平均値から離れていても、集団全体の平均値に与える影響は小さいため、結果の信頼性を高めることができます。例えば、一部の生徒の点数が極端に高くても、あるいは低くても、クラス全体の平均点には大きな影響を与えません。このため、一部の極端なデータに左右されず、集団全体の特徴を捉えるのに役立ちます。
計算の手間は比較的少ないため、多くのデータを抱える場合でも容易に適用できます。以前は計算機の性能が低く、大量のデータを扱うには時間がかかりましたが、近年の計算機の性能向上により、実用的な時間で計算を完了できるようになりました。手軽に計算できるため、様々な状況で活用しやすくなっています。
群平均法を適切に活用するためには、データの性質を理解することが重要です。例えば、集団の大きさが大きく異なる場合、平均値の比較だけでは正確な結論を導き出せない可能性があります。このような場合には、集団のばらつき具合も考慮に入れる必要があります。また、データが正規分布しているかどうかを確認することも大切です。正規分布していないデータに対して群平均法を適用すると、誤った解釈をしてしまう可能性があります。
群平均法は、様々な場面で活用できる強力な手法です。市場調査、医療統計、教育評価など、集団の比較が必要となる場面で広く使われています。それぞれの集団の特徴を捉え、比較することで、より深い洞察を得ることが可能になります。適切な手順で分析を行うことで、質の高い結果を得ることができ、意思決定の助けとなります。
| 項目 | 内容 |
|---|---|
| 定義 | 集団全体の平均値を計算し、それらを比較することで集団間の違いを明らかにする。 |
| 利点 | 外れ値の影響を受けにくい。計算の手間が少ない。 |
| 注意点 | 集団の大きさが大きく異なる場合は、ばらつき具合も考慮する。データが正規分布しているかを確認する。 |
| 活用例 | 市場調査、医療統計、教育評価 |
