遺伝的アルゴリズム:進化を模倣した最適化

AIを知りたい
先生、「遺伝的アルゴリズム」って、生き物の進化と関係があるって聞いたんですけど、どういうことですか?

AIエンジニア
そうだね。生き物は、環境に合うようにだんだん進化してきたよね。より環境に適した子孫を残すことで、強い遺伝子だけが生き残っていく。遺伝的アルゴリズムは、この仕組みをコンピューターで真似て、問題の最適な解を見つけ出す手法なんだ。

AIを知りたい
つまり、コンピューターの中で、色々な解をたくさん作って、良い解だけを残していくってことですか?

AIエンジニア
その通り!色々な解を遺伝子に見立てて、良い遺伝子を持つ解同士を組み合わせたり、突然変異を起こさせたりしながら、より良い解を世代交代で生み出していくんだ。そうやって、最終的に一番良い解を見つけ出すんだよ。
遺伝的アルゴリズムとは。
人工知能の分野で『遺伝的アルゴリズム』というものがあります。これは、自然界の生き物が進化し、遺伝していく仕組みを真似て作られたものです。生き物が環境に適応して生き延びてきた方法をコンピューターで再現し、より良い遺伝子の組み合わせを見つけ出す方法です。
はじめに

遺伝的計算手法は、人工知能の中でも、自然の仕組みをうまく取り込んだ興味深い方法です。この手法は、自然界における生物の進化と同じように、世代交代を繰り返すことで、複雑な問題の最適な答えを見つけ出すことができます。
この手法では、まず始めに、問題に対する様々な答えの候補をいくつか用意します。これらの候補は、まるで生物の遺伝子のように、数値や記号の組み合わせで表現されます。そして、これらの候補の中から、より良い答えに近いものを選び出します。この選択は、自然界で強い個体が生き残るように、問題に対する適合度に基づいて行われます。
選ばれた候補は、次の世代の親となります。親の遺伝子を組み合わせたり、少し変化させたりすることで、新しい候補が生まれます。これは、生物の繁殖や突然変異に相当します。こうして生まれた新しい候補は、前の世代よりも優れた答えを持っている可能性があります。
このような世代交代を何度も繰り返すことで、候補は徐々に最適な答えへと近づいていきます。まるで生物が環境に適応し進化していくように、計算機上で様々な答えを生み出し、より良い答えへと導いていくのです。
この遺伝的計算手法は、様々な分野で活用されています。例えば、工場の生産計画を最適化したり、新しい材料の設計を支援したり、機械学習のモデルを調整したりといった用途があります。このように、進化という概念を計算機の世界に取り入れた革新的な手法は、様々な問題解決に役立っています。
仕組み

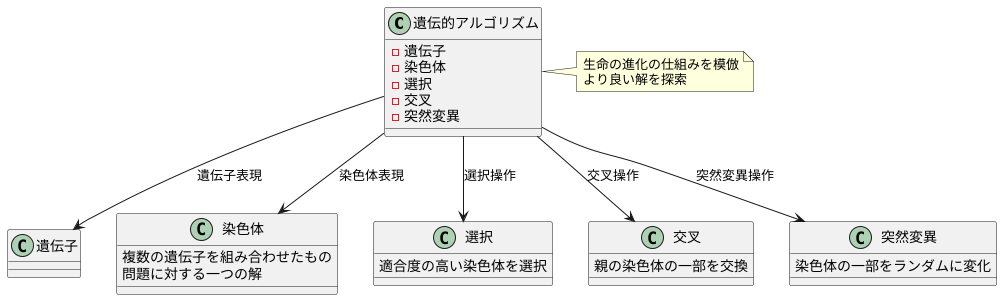
遺伝的アルゴリズムは、生命の進化に見られる遺伝の仕組みを模倣した計算手法です。その中心となる概念は、遺伝子、染色体、選択、交叉、突然変異です。これらの要素が複雑に絡み合いながら、より良い解を探索していきます。
まず、解きたい問題の答えを遺伝子という形で表現します。例えば、荷物の最適な詰め込み方を考える問題であれば、どの荷物をどの箱に入れるかという情報が遺伝子となります。複数の遺伝子を組み合わせたものが染色体です。染色体は、問題に対する一つの解を表しています。初期状態では、複数の染色体がランダムに作成されます。これは、様々な可能性を最初から検討できるようにするためです。
次に、それぞれの染色体の適合度を評価します。適合度とは、その染色体が表す解の良さを数値で表したものです。荷物の詰め込み方の例では、箱の中に隙間なく荷物が詰め込まれているほど、適合度が高くなります。適合度の計算方法は、解きたい問題によって異なります。
適合度の高い染色体は、より良い解を表していると判断されます。そこで、適合度の高い染色体を選び出し、それらを親として新しい染色体を作ります。この染色体の作成には、交叉と突然変異という二つの操作が用いられます。交叉は、二つの親の染色体の一部を交換する操作です。これにより、親の優れた性質を受け継いだ新しい染色体が生まれます。突然変異は、染色体の一部をランダムに変化させる操作です。これは、局所的な最適解に陥ることを防ぎ、より広範囲の解を探索するために必要です。
これらの選択、交叉、突然変異の操作を繰り返すことで、染色体の適合度は徐々に高くなっていきます。これは、生物の進化と同じように、より環境に適した個体が生き残っていく過程を模倣しています。最終的には、最も適合度の高い染色体が、問題の最適解として得られます。
利点

遺伝的アルゴリズムは、従来の最適化手法と比べて様々な利点を持つ、強力な探索手法です。まず、広範囲の探索能力が挙げられます。多くの従来手法は、最初の解の近辺を探索するため、最も良い解がその近辺にない場合、見つけることができません。局所的な最適解、つまり、その近辺では最も良い解であっても全体で見ると最も良い解ではないものに捕らわれてしまうのです。一方、遺伝的アルゴリズムは、複数の解の候補、いわば様々な遺伝子を持つ個体の集団から探索を始めます。そして、それらを組み合わせたり変化させたりすることで、新しい解を生み出していきます。この多様性を持った集団からの探索は、局所的な最適解に捕らわれにくく、より広い範囲を探索することを可能にします。そのため、全体で最も良い解、いわゆる大局的最適解を見つけられる可能性が高いのです。
次に、並列処理による計算時間の短縮が挙げられます。遺伝的アルゴリズムでは、個体集団のそれぞれの個体を同時に評価することができます。従来手法では、多くの場合、解の候補を一つずつ評価していく必要がありました。しかし、遺伝的アルゴリズムは、複数の個体を同時に処理できるため、計算時間を大幅に短縮できます。これは、特に大規模で複雑な問題を扱う際に大きな利点となります。
さらに、遺伝的アルゴリズムは、様々な種類の問題に適用できる汎用性も持ち合わせています。遺伝的アルゴリズムは、解を遺伝子のようなデータ列で表現し、それを操作することで新しい解を生み出します。この解の表現方法を工夫することで、様々な最適化問題に対応できます。例えば、数値を組み合わせた数列で表現したり、順番を表す並びで表現したり、様々な表現方法が考えられます。そのため、特定の分野に限定されず、様々な分野の最適化問題に適用できるのです。これらの利点により、遺伝的アルゴリズムは、工学、経済、生物学など、幅広い分野で注目され、活用されています。
| 利点 | 説明 |
|---|---|
| 広範囲の探索能力 | 複数の解の候補から探索を始め、局所的な最適解に捕らわれにくく、大局的最適解を見つけられる可能性が高い。 |
| 並列処理による計算時間の短縮 | 個体集団のそれぞれの個体を同時に評価することで、計算時間を大幅に短縮できる。 |
| 様々な種類の問題に適用できる汎用性 | 解を遺伝子のようなデータ列で表現し、それを操作することで新しい解を生み出すため、様々な最適化問題に対応できる。 |
応用例

遺伝的アルゴリズムは、生物の進化を模倣した計算手法であり、様々な分野で応用されています。その適用範囲は広く、工場の生産計画、商品の配送経路、新薬開発における分子の設計、機械学習における最適な設定値の探索など、多様な問題解決に役立っています。
例えば、工場では、限られた資源と時間の中で、製品を効率的に生産するための最適な計画を立てる必要があります。従来の手法では、複雑な条件下での最適な計画を立てることが難しかったのですが、遺伝的アルゴリズムを用いることで、より効率的な生産計画を導き出すことが可能になります。
また、配送ルートの最適化も重要な応用例です。多くの地点を巡回する際に、最短距離で移動するための経路を見つけることは、燃料消費の削減や配送時間の短縮につながります。遺伝的アルゴリズムは、膨大な数の経路の中から、最適な経路を効率的に探索することができます。
創薬の分野では、病気の原因となるたんぱく質に作用する薬剤の分子構造を設計する際に、遺伝的アルゴリズムが活用されています。膨大な数の分子構造の中から、効果的な薬剤の候補となる分子構造を探索することで、新薬開発の効率化に貢献しています。
さらに、機械学習の分野では、学習モデルの性能を最大限に引き出すための最適な設定値を見つけるために、遺伝的アルゴリズムが用いられています。従来の手法では、最適な設定値を見つけることが困難でしたが、遺伝的アルゴリズムを用いることで、より効率的に最適な設定値を探索することが可能になり、機械学習モデルの性能向上に役立っています。
近年では、人工知能技術の発展に伴い、遺伝的アルゴリズムと深層学習を組み合わせるなど、新たな手法も開発されており、今後ますます応用範囲が広がる遺伝的アルゴリズムは、様々な分野で革新的な進歩をもたらす可能性を秘めています。
| 分野 | 適用例 | 効果 |
|---|---|---|
| 工場 | 生産計画の最適化 | 資源と時間の制約下での効率的な生産 |
| 物流 | 配送ルートの最適化 | 燃料消費の削減、配送時間の短縮 |
| 創薬 | 薬剤分子構造の設計 | 新薬開発の効率化 |
| 機械学習 | 学習モデルの最適な設定値探索 | モデル性能の向上 |
課題

遺伝的アルゴリズムは、生物の進化を模倣した最適化手法であり、様々な分野で活用されています。しかし、その強力さの一方で、いくつかの難題も抱えています。
まず、適切な設定値を見つけるのが難しいという問題があります。遺伝的アルゴリズムは、親から子へ遺伝情報が受け継がれる際に、遺伝子の組み合わせを変える「交叉」と、遺伝子が変化する「突然変異」を繰り返すことで、より良い解を見つけ出そうとします。この交叉や突然変異が起こる割合は、あらかじめ設定する必要があります。しかし、これらの設定値は問題の種類や規模によって大きく異なり、最適な値を見つけるのは容易ではありません。設定値が適切でないと、なかなか良い解が見つからないばかりか、膨大な時間がかかってしまうこともあります。
次に、解の表現方法を工夫する必要があるという問題があります。遺伝的アルゴリズムでは、解を遺伝子という形で表現します。例えば、巡回セールスマン問題であれば、訪れる都市の順番を遺伝子で表現します。しかし、問題によっては、解を遺伝子で表現するのが難しい場合があります。また、表現方法が適切でないと、良い解が得られない可能性があります。
最後に、計算に時間がかかるという問題があります。遺伝的アルゴリズムは、交叉と突然変異を何度も繰り返すことで、徐々に良い解に近づいていきます。そのため、問題の規模が大きくなると、計算量も増大し、非常に長い時間がかかることがあります。特に、解の候補が多い問題では、実用的な時間内に解を得ることが難しい場合もあります。
これらの難題を解決するために、様々な研究が行われています。例えば、設定値を自動的に調整する手法や、より効率的な遺伝子表現方法などが提案されています。また、計算時間を短縮するために、並列計算技術の活用なども進められています。遺伝的アルゴリズムは、まだまだ発展途上の技術であり、今後の更なる進歩が期待されます。
| 難題 | 詳細 |
|---|---|
| 適切な設定値を見つけるのが難しい | 交叉や突然変異の割合といった設定値は問題の種類や規模によって大きく異なり、最適な値を見つけるのは容易ではない。不適切な設定値は良い解の発見を阻害し、計算時間を増大させる可能性がある。 |
| 解の表現方法を工夫する必要がある | 解を遺伝子で表現する必要があるが、問題によってはそれが難しい場合がある。また、表現方法の適切さが解の質に影響する。 |
| 計算に時間がかかる | 交叉と突然変異の反復により徐々に最適解に近づくため、問題の規模が大きくなると計算量が増大し、計算時間が長くなる。特に解の候補が多い問題では、実用的な時間内に解を得るのが難しい場合もある。 |
まとめ

遺伝的アルゴリズムは、生物の進化に見られる自然淘汰の仕組みを模倣した計算手法です。様々な問題の最適解を見つけ出すために用いられます。まるで生物が世代交代を繰り返しながら環境に適応していくように、遺伝的アルゴリズムも試行錯誤を通じて最適な解へと近づいていきます。
このアルゴリズムは、まずランダムに生成された複数の解の候補を用意することから始まります。これらの候補は、生物の遺伝子に相当するものと考えられます。そして、それぞれの候補が持つ性質に基づいて、どの候補がより良い解に近いかを評価します。この評価方法は、解きたい問題によって異なります。
評価が終わると、より良い評価を得た候補が次の世代に残る、あるいはより多くの子孫を残すように選択されます。これは自然界でより環境に適応した個体が生き残りやすいのと同じです。また、遺伝子に相当するデータの一部を他の候補と交換する「交叉」や、ランダムにデータの一部を変化させる「突然変異」といった操作も加えられます。これらの操作により、新たな解の候補が生成され、多様性を維持しながら最適解の探索が行われます。
遺伝的アルゴリズムには、広範囲の探索が可能であること、複数の計算を同時に行う並列処理に適していること、様々な種類の問題に応用できる汎用性の高さといった利点があります。そのため、工学設計、機械学習、経済分析など、幅広い分野で利用されています。
一方で、アルゴリズムをうまく動作させるためのパラメータ設定が難しいという課題もあります。また、問題を遺伝的アルゴリズムで解ける形に落とし込む方法を見つけるのが難しい場合もあります。さらに、多くの計算が必要となるため、計算時間が長くなる可能性もあります。これらの課題は、今後の研究によって解決されていくことが期待されています。生物の進化という自然の摂理を計算機で再現するという壮大な試みは、これからも多くの研究者を惹きつけ、さらなる発展を遂げていくことでしょう。
| 項目 | 内容 |
|---|---|
| 概要 | 生物の進化の仕組みを模倣した最適解探索アルゴリズム |
| 手順 | 1. ランダムに解の候補を生成 2. 各候補を評価 3. 優れた候補を選択 4. 交叉と突然変異で新たな候補生成 5. 繰り返す |
| 利点 | 広範囲探索可能、並列処理に適する、汎用性が高い |
| 応用分野 | 工学設計、機械学習、経済分析など |
| 課題 | パラメータ設定が難しい、問題の適用方法、計算時間の長さ |
