汎化誤差:機械学習の精度を高める鍵

AIを知りたい
『汎化誤差』って、よく聞くけれど、実際どういう意味で、なぜ重要なんですか?

AIエンジニア
いい質問だね。たとえば、たくさんの練習問題を解いてテストに臨んだとします。練習問題の点数はすごくいい。これが『訓練誤差』にあたります。でも、本番のテストでは、練習問題とは違う初めての問題が出るよね?そこでどれだけ点数を取れるかが『汎化誤差』なんだ。

AIを知りたい
なるほど。練習問題だけできても、本番で点が取れないと意味がないってことですね。でも、AIとどう関係があるんですか?

AIエンジニア
AIもたくさんのデータで学習する。練習問題を解くようにね。AIの目標は、学習に使っていないデータに対しても、正しい予測をすること。つまり、『汎化誤差』を小さくすることなんだ。これが重要じゃないと、現実の問題で役に立たないAIになってしまうからね。
汎化誤差とは。
人工知能の分野でよく使われる「汎化誤差」について説明します。汎化誤差とは、まだ学習していない、未知のデータに対してどのくらい予測が外れるかを表す尺度です。学習済みのデータに対する誤差である「訓練誤差」とは違います。学習を進めていくと、過学習といった現象が起こり、汎化誤差が大きくなってしまうことがあります。これは、既に学習したデータにはよく当てはまるようになっても、新しいデータに対しては予測が大きく外れてしまう状態です。そのため、機械学習を行う際には、この汎化誤差をなるべく小さくすることが非常に重要になります。
汎化誤差とは

機械学習の目的は、現実世界の問題を解決できる賢い模型を作ることです。その賢さを測る物差しの一つが「汎化誤差」です。
模型を作るには、まず教科書となる学習データを使って模型に勉強させます。学習データに対する誤差は「学習誤差」と呼ばれ、学習データだけを完璧に覚えたとしても、それは賢い模型とは言えません。本当に賢い模型は、初めて見る問題にもうまく対応できる模型です。この初めて見る問題を「未知データ」と言い、未知データに対する誤差が「汎化誤差」です。
汎化誤差とは、未知データに直面した際に、模型の予測がどれくらい正確かを表す指標です。この誤差が小さければ小さいほど、模型は様々な状況で安定した性能を発揮できると期待できます。逆に、学習データに特化しすぎて未知データへの対応力が低いと、汎化誤差は大きくなります。これは「過学習」と呼ばれる状態で、まるで試験問題を丸暗記しただけで、応用問題が解けない生徒のような状態です。
機械学習模型開発においては、この汎化誤差をいかに小さく抑えるかが、模型の精度向上に直結する重要な課題となります。学習データに過剰に適応することなく、未知データにも対応できる能力、すなわち汎化能力を高めることが求められます。そのためには、学習データの量や質を調整したり、模型の複雑さを適切に制御したりするなど、様々な工夫が必要となります。汎化誤差を小さくすることで、より信頼性が高く、実用的な機械学習模型を開発することが可能になります。
| 項目 | 説明 |
|---|---|
| 機械学習の目的 | 現実世界の問題を解決できる賢い模型を作ること |
| 賢さの指標 | 汎化誤差 |
| 学習データ | 模型の学習に用いるデータ |
| 学習誤差 | 学習データに対する誤差 |
| 未知データ | 初めて見る問題データ |
| 汎化誤差 | 未知データに対する誤差。模型の予測精度を表す指標 |
| 汎化誤差が小さい | 様々な状況で安定した性能 |
| 汎化誤差が大きい | 過学習(学習データに特化しすぎ、未知データへの対応力低い) |
| 機械学習模型開発の課題 | 汎化誤差を小さく抑える |
| 汎化能力を高める方法 | 学習データの量や質の調整、模型の複雑さを適切に制御 |
訓練誤差との違い

機械学習では、作った模型がどれだけうまく働くかを見極めることが大切です。このとき、よく似た二つの考え方、「訓練誤差」と「汎化誤差」を理解する必要があります。この二つは似て非なるものなので、混同しないように注意が必要です。
まず、訓練誤差とは、模型の学習に用いたデータに対して、どれだけ模型の予測がずれているかを表すものです。模型を作る際には、たくさんの例題と答えをセットで与えて学習させます。この例題と答えのセットを訓練データと呼びます。学習を進めるにつれて、模型は訓練データの特徴をうまく捉えられるようになり、訓練データに対する誤差、つまり訓練誤差は小さくなります。これは、いわば練習問題を繰り返し解くことで正解率が上がっていくようなものです。
しかし、訓練誤差が小さくなったからといって、その模型が本当に役立つとは限りません。なぜなら、模型の本当の目的は、未知のデータに対しても正しく予測することだからです。この未知のデータに対する予測能力を測る指標が汎化誤差です。
訓練誤差を小さくすることに集中しすぎると、「過学習」という状態に陥ることがあります。これは、模型が訓練データに過剰に適応しすぎてしまい、訓練データでは高い正答率を示すにも関わらず、新しいデータに対してはうまく対応できない状態です。例えるなら、練習問題では満点を取れるのに、本番の試験では全く点が取れないような状態です。
本当に使える模型を作るには、訓練誤差だけでなく汎化誤差にも注目しなければなりません。訓練誤差が小さく、かつ汎化誤差も小さい、つまり、既知のデータにも未知のデータにも対応できる模型を作ることを目指す必要があります。そのためには、様々な工夫や検証が必要になります。まさに、本番で力を発揮できるよう、バランスの良い学習が求められるのです。
| 指標 | 説明 | 意味 | 問題点 |
|---|---|---|---|
| 訓練誤差 | 学習に用いたデータに対する予測のずれ | 学習データへの適合度 | 過学習の可能性 |
| 汎化誤差 | 未知のデータに対する予測能力 | 実用性、新しいデータへの対応力 | 測定が難しい |
汎化誤差を小さくする方法

機械学習モデルを作る上で、学習に使っていないデータに対しても高い精度で予測できること、これがとても重要です。この能力のことを汎化性能と呼び、学習データと未知のデータでの精度の差を汎化誤差と言います。この汎化誤差を小さくする、つまり未知のデータにもうまく対応できるモデルを作るには、幾つかの方法があります。
まず、モデルが学習データに過剰に適合してしまう過学習を防ぐことが大切です。この過学習を防ぐための代表的な方法の一つに正則化があります。正則化とは、モデルの複雑さに制限を加えることで、過学習を抑える技術です。複雑すぎるモデルは学習データの細かな特徴まで捉えてしまい、未知のデータには対応できなくなってしまいます。正則化は、このモデルの複雑さに「罰則」を与えることで、過剰な適合を防ぎ、汎化性能を向上させます。
次に、交差検証も有効な方法です。限られた学習データを有効に活用するために、学習データを複数のグループに分け、それぞれのグループでモデルを学習・評価することを繰り返します。各グループで得られた評価結果の平均をとることで、モデルの汎化性能をより正確に見積もることができます。これは、限られたデータでより信頼性の高い評価を行うための工夫と言えるでしょう。
最後に、データ拡張も重要な手法です。これは、既存のデータに様々な変換を加えることで、学習データの量を人工的に増やす技術です。例えば、画像データであれば、回転、反転、明るさの調整などを行うことで、元データとは異なる新たな画像データを生成できます。データを増やすことで、モデルはより多様なデータに接し、過学習のリスクを減らしながら、より汎化性能の高いモデルを学習できます。
正則化、交差検証、データ拡張、これらを適切に組み合わせることで、汎化誤差を効果的に小さくし、モデルの精度を高めることができます。ただし、どの手法が最も効果的かは、扱うデータやモデルの種類によって大きく変わるため、実際に試しながら最適な組み合わせを見つけることが重要です。
| 手法 | 説明 | 目的 |
|---|---|---|
| 正則化 | モデルの複雑さに制限を加えることで過学習を抑える技術。モデルの複雑さに「罰則」を与える。 | 過学習を防ぎ、汎化性能を向上させる。 |
| 交差検証 | 学習データを複数のグループに分け、各グループでモデルを学習・評価し、結果の平均をとる。 | 限られたデータでモデルの汎化性能をより正確に見積もる。 |
| データ拡張 | 既存のデータに様々な変換を加えることで、学習データの量を人工的に増やす。 | モデルがより多様なデータに接することで、過学習リスクを減らし、汎化性能を高める。 |
汎化誤差の評価方法

機械学習の目的は、未知のデータに対しても正しく予測できるモデルを作ることです。この未知のデータに対する予測能力を測る指標が汎化誤差です。 汎化誤差を正しく評価することは、モデルの性能を把握し、より良いモデルを作る上で非常に重要です。
汎化誤差を測るためには、学習に使っていないデータが必要です。そこで、手持ちのデータを学習用とテスト用に分割します。学習用データでモデルを訓練し、そのモデルにテスト用データを与えて予測させます。このテスト用データに対する予測の誤差が、汎化誤差の推定値となります。
例えば、ある果物の重さから糖度を予測するモデルを作りたいとします。集めたデータを学習用とテスト用に分け、学習用データで重さと糖度の関係を学習させます。学習が終わったら、テスト用データの果物の重さを入力し、糖度を予測させます。この予測値と実際の糖度の差が、このモデルの汎化誤差を示す一つの指標となります。
交差検証という手法を使うと、より信頼性の高い汎化誤差の推定値を得られます。交差検証では、学習データをいくつかのグループに分割します。そして、一つのグループをテスト用データ、残りのグループを学習用データとしてモデルを訓練します。この手順を、各グループが一度ずつテスト用データになるように繰り返します。それぞれのグループで得られた誤差の平均を計算することで、最終的な汎化誤差の推定値とします。
交差検証は、限られた量のデータからより多くの情報を引き出し、モデルの汎化性能をより正確に見積もるのに役立ちます。このように、目的に応じて適切な評価方法を選ぶことで、モデルの真の性能をより良く理解し、改良につなげることができるのです。
機械学習における重要性

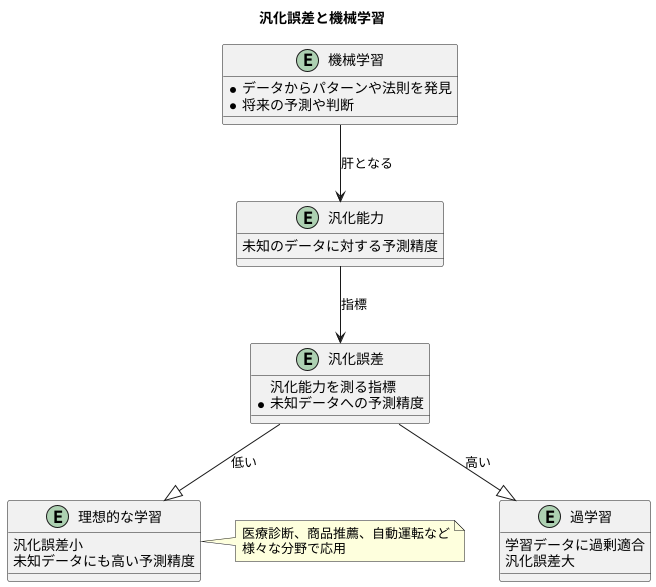
機械学習は、まるで人が学ぶように、計算機にデータからパターンや法則を見つけ出させ、将来の予測や判断に役立てる技術です。この技術の肝となるのが、未知のデータに対しても正確な予測ができる能力、すなわち汎化能力です。この汎化能力を測る指標が汎化誤差であり、機械学習の世界ではこの誤差をいかに小さくするかが大きな課題となっています。
汎化誤差とは、学習に使っていないデータに対して、モデルがどれくらい正確に予測できるかを表す尺度です。学習に用いたデータのみで高い精度を出せても、新しいデータに対して全く予測できないモデルでは意味がありません。例えるなら、教科書の内容は全て暗記できるのに、テストで応用問題が出されると全く解けない生徒のようなものです。このような状態は過学習と呼ばれ、機械学習では避けなければいけない状態の一つです。過学習が起きると、モデルは学習データの些細な特徴にまで過剰に適合してしまい、真の法則を見失ってしまうのです。その結果、未知のデータに対する予測精度が著しく低下します。
反対に、汎化誤差が小さいモデルは、学習データから本質的な法則を抽出し、未知のデータに対しても高い予測精度を維持できます。これは、様々な問題に対応できる応用力の高い生徒と言えるでしょう。このようなモデルこそが、現実世界の問題解決に役立ち、真に価値のあるものとなります。例えば、医療診断、商品推薦、自動運転など、様々な分野で機械学習が活用されていますが、これらの応用で信頼性の高い結果を得るためには、汎化誤差の小さいモデルを構築することが不可欠です。
機械学習モデルの開発においては、常に汎化誤差を念頭に置き、それを最小限にするための様々な工夫が凝らされています。学習データの量や質を調整したり、モデルの複雑さを制御するといった手法を用いることで、過学習を防ぎ、汎化能力の高いモデルを構築することが目指されています。このように、汎化誤差は機械学習の成否を左右する重要な要素であり、より良いモデルを開発するための鍵を握っていると言えるでしょう。