汎化誤差:機械学習の鍵

AIを知りたい
先生、「汎化誤差」って、よくわからないんですけど、簡単に教えてもらえますか?

AIエンジニア
わかったよ。「汎化誤差」とは、まだ学習していない、見たことのない新しいデータに対して、AIがどれくらい間違えるかを示す尺度のことだよ。例えるなら、算数のテストで、練習問題と同じような問題なら解けるけど、ちょっとひねった応用問題になると解けなくなる、そんな感じだね。

AIを知りたい
なるほど。練習問題ばかり解いて応用問題を解けないのは、まさに「汎化誤差」が大きいってことですね。では、どうすれば「汎化誤差」を小さくできるんですか?

AIエンジニア
いい質問だね。「汎化誤差」を小さくするには、学習データを増やしたり、AIの仕組みを調整したりする必要があるんだ。例えば、算数のテストなら、色々な種類の問題をたくさん解く練習をしたり、問題の解き方のコツを学ぶことで、応用問題にも対応できるようになるよね。それと似ているんだよ。
汎化誤差とは。
人工知能で使われる言葉に「汎化誤差」というものがあります。これは、まだ学習していないデータに対してどれだけ予測がずれるかを示すものです。学習を進めていくと、訓練誤差(学習に使ったデータに対するずれ)は小さくなりますが、汎化誤差は逆に大きくなることがあります。これは、学習しすぎて、知っているデータにだけ過剰に合わせすぎてしまう「過学習」が起きるためです。過学習が起きると、未知のデータに対しては大きく予測が外れてしまうのです。機械学習を行う上で、この汎化誤差をなるべく小さくすることが非常に大切です。
汎化誤差とは

機械学習の最終目標は、初めて出会うデータに対しても高い予測精度を誇るモデルを作ることです。この未知のデータに対する予測能力を測る重要な指標こそが、汎化誤差です。
汎化誤差とは、学習に使っていない全く新しいデータに対して、モデルがどれほど正確に予測できるかを示す尺度です。言い換えると、作り上げたモデルがどれほど実世界の様々な問題に役立つかを評価する指標と言えるでしょう。
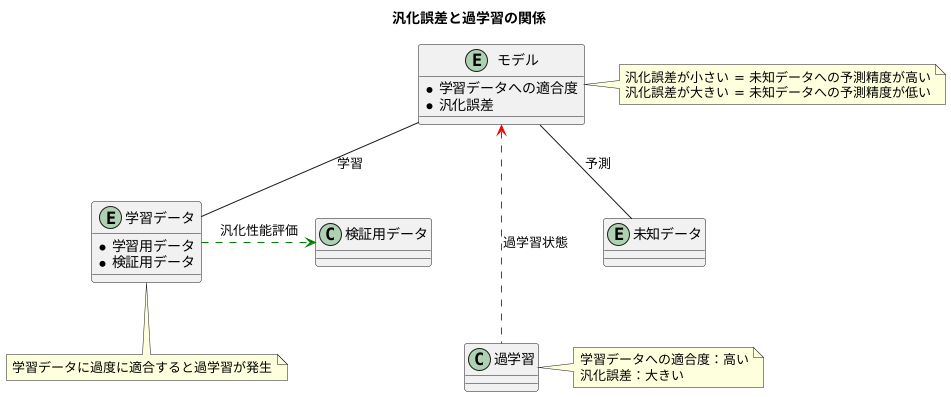
モデルを作る際には、大量のデータを使って学習させますが、この学習データにあまりにもぴったりと合わせてモデルを作ってしまうと、思わぬ落とし穴にはまります。学習データに対しては非常に高い予測精度を示すにもかかわらず、新しいデータに対しては予測が全く外れてしまう、という現象が起こるのです。このような状態を過学習と呼びます。
過学習が起きると、学習データに対する予測精度は非常に高い一方で、汎化誤差は大きくなってしまいます。つまり、見たことのないデータに対する予測能力が著しく低下してしまうのです。これは、まるで特定の試験問題の解答だけを丸暗記した生徒が、少し問題文が変わっただけで全く解けなくなってしまう状況に似ています。試験問題にぴったりと合わせた学習は、一見素晴らしい結果をもたらすように見えますが、応用力が全く養われていないため、真の学力とは言えません。
機械学習モデルの開発においても同様に、汎化誤差を小さく抑え、未知のデータに対しても高い予測精度を持つモデルを作ることが重要です。そのためには、学習データだけに過度に適応しないように、様々な工夫を凝らす必要があります。
例えば、学習データの一部を検証用に取っておき、モデルの汎化性能を定期的に確認する方法があります。また、モデルが複雑になりすぎないように、あえて制限を加える方法も有効です。
このように、汎化誤差を意識することは、高性能な機械学習モデルを開発する上で欠かせない要素と言えるでしょう。
訓練誤差との違い

学習に使ったデータに対する予測の正確さを示す指標を訓練誤差と言います。作った模型が、学習に使ったデータに対してどれくらい正確に予測できるかを表すものです。模型は学習に使ったデータを使って作られるため、訓練誤差が小さければ小さいほど、そのデータに対する予測の精度は上がります。しかし、訓練誤差が小さいからと言って、まだ学習していない未知のデータに対しても正確に予測できるとは限りません。これは、汎化誤差と呼ばれる指標と深く関わっています。汎化誤差は、学習に使っていないデータに対する予測の正確さを示す指標です。
例を挙げると、特定の試験問題と解答だけを丸暗記した生徒を想像してみてください。この生徒は、丸暗記した試験問題に対しては満点を取ることができるでしょう。これは訓練誤差が非常に小さい状態です。しかし、同じ教科でも少し違う問題や応用問題が出題された場合、この生徒は全く対応できない可能性があります。これは、汎化誤差が大きい状態を表しています。つまり、丸暗記したデータ以外への対応力は低いということです。
真に優れた模型を作るには、訓練誤差と汎化誤差の両方を考慮する必要があります。訓練誤差が小さくても汎化誤差が大きい模型は、特定のデータに特化しすぎてしまい、未知のデータへの対応力が低いと言えます。まるで試験問題を丸暗記した生徒のように、応用力が欠けているのです。反対に、汎化誤差が小さい模型は、学習に使ったデータ以外にも対応できる、柔軟性と応用力を備えていると言えます。これは、教科の原理や法則を理解している生徒が、様々な問題に対応できるのと同じです。ですから、本当に優れた模型とは、学習に使ったデータだけでなく、未知のデータに対しても高い予測精度を示す必要があり、そのためには汎化誤差を小さくすることが重要となります。
| 指標 | 説明 | 例 |
|---|---|---|
| 訓練誤差 | 学習に使ったデータに対する予測の正確さを示す指標。 | 特定の試験問題と解答を丸暗記した生徒が、その試験問題に対して満点を取れる。 |
| 汎化誤差 | 学習に使っていないデータに対する予測の正確さを示す指標。 | 丸暗記した生徒が、少し違う問題や応用問題に対応できない。 |
汎化誤差を小さくするには

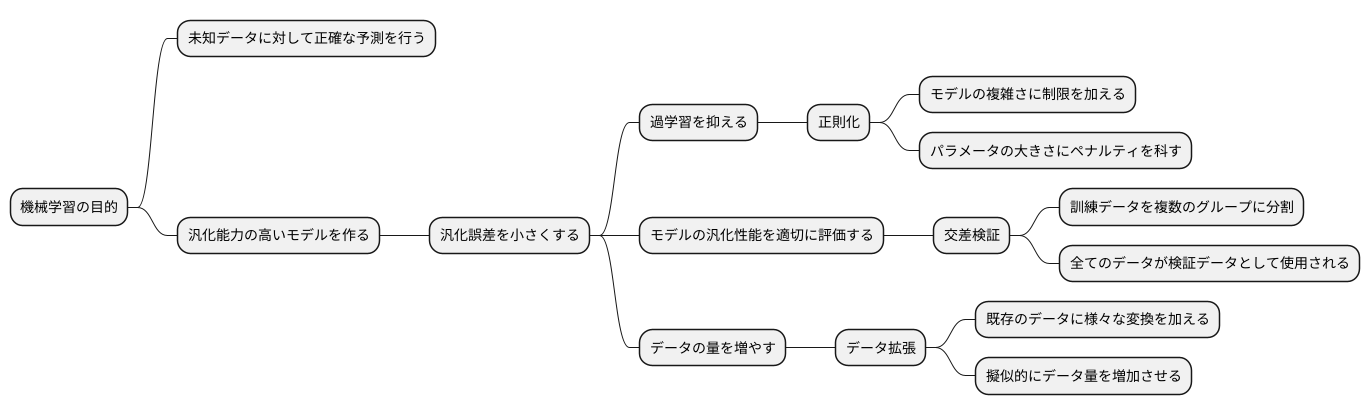
機械学習の目的は、未知のデータに対して正確な予測を行う、汎化能力の高いモデルを作ることです。この未知データに対する予測の誤差を汎化誤差と呼び、この値を小さくすることがモデル構築の重要な課題となります。汎化誤差を小さくするためには、様々な工夫が凝らされています。
まず、過学習を抑えることが重要です。過学習とは、訓練データに過度に適合しすぎてしまい、未知データへの対応力が低下する現象です。この過学習を防ぐ代表的な手法が正則化です。正則化とは、モデルの複雑さに制限を加えることで、過学習を抑制する手法です。具体的には、モデルのパラメータの大きさにペナルティを科すことで、パラメータが過度に大きくなることを防ぎます。結果として、モデルは滑らかな曲線となり、未知のデータにも対応しやすくなります。
次に、モデルの汎化性能を適切に評価する必要があります。そこで用いられるのが交差検証です。交差検証では、訓練データを複数のグループに分割し、あるグループを検証データ、残りのグループを訓練データとしてモデルを学習させます。この検証データを順次変更していくことで、全てのデータが検証データとして使用されます。こうして得られた複数の評価結果を平均することで、モデルの汎化性能をより正確に見積もることができます。
最後に、データの量を増やすことも有効です。データが多いほど、モデルはデータの背後にある規則性をより正確に学習できます。しかし、実際には十分なデータ量を確保することが難しい場合もあります。そこで、データ拡張と呼ばれる手法が用いられます。データ拡張とは、既存のデータに様々な変換を加えることで、擬似的にデータ量を増加させる手法です。例えば、画像データであれば、回転、反転、拡大縮小などの変換を加えることで、元データとは異なる新たなデータを生成することができます。
これらの正則化、交差検証、データ拡張といった手法を適切に用いることで、汎化誤差の小さな、つまり未知データに対しても高い予測精度を持つモデルを構築することができます。
汎化誤差の評価

機械学習の目的は、未知のデータに対しても高い予測精度を持つモデルを作ることです。この未知のデータに対する予測精度を測る尺度が汎化誤差です。汎化誤差を正しく評価することは、モデルの性能を測る上で非常に大切です。
汎化誤差を評価するためには、学習に利用していないデータが必要です。これらのデータは、大きく分けて検証データとテストデータの2種類があります。
検証データは、文字通りモデルの性能を検証するためのデータです。具体的には、様々な設定値(ハイパーパラメータと呼ばれます)の中から、最も良いモデルを選ぶために使われます。例えば、ある予測モデルを作る際に、予測の複雑さを調整するパラメータがあるとします。このパラメータの値を様々に変えながらモデルを学習し、それぞれのモデルを検証データで評価することで、最適なパラメータ値を見つけ出します。
テストデータは、最終的なモデルの性能を測るために使われます。検証データでハイパーパラメータを調整した最終的なモデルを、一度だけテストデータに適用し、その性能を評価します。テストデータは一度しか使わないため、テストデータでの性能はまさに未知のデータに対する性能を反映していると考えられます。
汎化誤差を評価する際には、目的に合った指標を用いることが重要です。例えば、分類問題では、正解率、適合率、再現率などが用いられます。正解率は、全体のデータの中で正しく分類できた割合を表します。適合率は、陽性と予測したデータの中で実際に陽性だった割合を表します。再現率は、実際に陽性のデータの中で陽性と予測できた割合を表します。状況に応じて適切な指標を選ぶ必要があります。
回帰問題では、平均二乗誤差などが用いられます。平均二乗誤差は、予測値と実測値の差の二乗の平均を表します。
このように、検証データとテストデータを適切に用い、目的に合った指標を用いることで、モデルの汎化性能を客観的に測ることができます。そして、その評価結果に基づいてモデルを改善していくことで、より精度の高い予測モデルを作ることが可能になります。
| データの種類 | 目的 | 使用方法 | 評価指標(例) |
|---|---|---|---|
| 学習データ | モデルの学習 | モデルのパラメータを調整するために使用 | – |
| 検証データ | モデルの性能検証 | 様々なハイパーパラメータの中から最適なモデルを選択するために使用 | 分類問題:正解率、適合率、再現率など 回帰問題:平均二乗誤差など |
| テストデータ | 最終的なモデルの性能評価 | 最終モデルの汎化性能を評価するために一度だけ使用 | 分類問題:正解率、適合率、再現率など 回帰問題:平均二乗誤差など |
機械学習における重要性

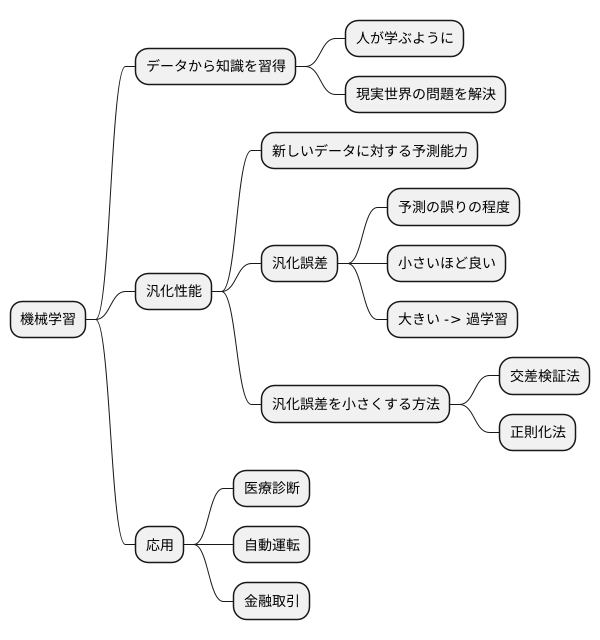
機械学習は、まるで人が学ぶように、コンピュータにデータから知識を習得させる技術です。この技術の最終的な目的は、現実世界の問題を解決する、役に立つ道具を作ることにあります。つまり、ただ単に与えられたデータにうまく対応できるだけでなく、まだ見たことのない新しいデータに対しても正確な予測ができる能力、すなわち汎化性能が非常に重要になります。
この汎化性能を測る物差しとなるのが汎化誤差です。新しいデータに対する予測の誤りの程度を示すこの値は、機械学習モデルの開発において中心的な役割を担っています。汎化誤差が小さければ小さいほど、そのモデルは未知のデータに対しても高い精度で予測できる、信頼性の高いモデルと言えるでしょう。逆に、汎化誤差が大きい場合は、モデルが学習データの特徴を捉えすぎてしまい、新しいデータにうまく対応できない「過学習」と呼ばれる状態に陥っている可能性があります。
汎化誤差を小さくするためには、様々な工夫が凝らされています。例えば、学習データの一部をモデルの評価に用いる交差検証法や、モデルの複雑さを調整する正則化法など、様々な手法が開発され、活用されています。これらの手法を適切に用いることで、過学習を防ぎ、より汎化性能の高い、実用的なモデルを構築することが可能になります。
このように、汎化誤差を理解し、それを最小化する努力は、機械学習の根幹を成す重要な要素と言えるでしょう。医療診断や自動運転、金融取引など、様々な分野で機械学習が実用化されていますが、これらの応用において、信頼性の高い予測結果を提供するためには、汎化誤差の制御が不可欠です。機械学習の進歩は、まさにこの汎化誤差との戦いと言えるかもしれません。