探索と活用:バンディットアルゴリズム

AIを知りたい
先生、「バンディットアルゴリズム」って難しそうだけど、どんなものか簡単に教えてもらえますか?

AIエンジニア
そうだね。簡単に言うと、限られた情報の中で、試行錯誤しながら一番良い結果を探し出す方法だよ。たとえば、新しいお菓子をいくつか作って、どれが一番売れるか試したいとする。いくつかのお店で、それぞれ違うお菓子を売ってみる。売れたお菓子の情報が集まれば、次はそのお菓子をたくさん作ればいいよね。

AIを知りたい
なるほど。でも、ずっと売れ行きを試していると、売れないお菓子はずっと売れないままですよね?

AIエンジニア
その通り。だから、時々売れていないお菓子も売ってみるんだ。もしかしたら、売れるお店もあるかもしれないからね。このように、すでに知っている情報を使うことと、新しい情報を得ることをうまくバランスをとるのがバンディットアルゴリズムの大切なところなんだよ。
バンディットアルゴリズムとは。
人工知能で使われる『バンディットアルゴリズム』について説明します。バンディットアルゴリズムは、試行錯誤を通じて学習していく方法のひとつです。ウェブサイトなどでは、情報が少ない状態でも一番良い結果を出さなければなりません。このアルゴリズムは、経験を積むための『探索』と、これまでの経験を活かす『予測』をうまく調整することで、最良の選択を見つけ出そうとします。例えば、ある利用者には実績のある方法でサービスを提供し、別の利用者にはまだよく分からない方法でサービスを提供して、その結果を参考にしながら、より良いサービスの提供方法を学習していきます。
はじめに

今や誰もが使うようになったインターネットを通じて、様々な情報が飛び交う時代になりました。多くの事業者が、自社の持つ情報網や様々な道具を通して情報を発信し、利用者の満足度を高めるための努力を続けています。より良い品物や仕組みを提供するために、様々な工夫が凝らされています。
そうした中で、限られた材料から、最も良い結果を導き出すための方法として、注目されているのが「バンディット計算手順」です。まるで限られた道具で財宝を探し出す盗賊のように、この計算手順は、少ない情報からでも、繰り返し試行錯誤することで、最も良い行動を学ぶことができるのです。
たとえば、ある買い物場所に来た客に、いくつかのお菓子を勧める場面を想像してみてください。お店側は、どの商品が最も売れるかを知りたいと思っています。しかし、全てのお菓子を全ての人に試してもらうことはできません。そこで、この計算手順を利用します。最初は手探りでいくつかのお菓子を勧めてみます。そして、お客さんがどの商品を選んだかという情報をもとに、売れ筋のお菓子を予測していきます。
この計算手順の優れた点は、情報が少ない段階でも、試行錯誤を通して学習し、徐々に最適な選択に近づいていくことができる点です。新しいお菓子が追加された場合でも、柔軟に対応し、人気商品を素早く見つけることができます。限られた情報から最良の結果を導き出す、まさに現代社会に必要な技術と言えるでしょう。
| 名称 | 概要 | 例 |
|---|---|---|
| バンディット計算手順 | 限られた材料から最良の結果を導き出す方法。少ない情報からでも、繰り返し試行錯誤することで、最も良い行動を学ぶ。 | 買い物客へのお菓子のおすすめ |
| 目的 | より良い品物や仕組みを提供し、利用者の満足度を高める。 | 最も売れるお菓子を見つける。 |
| 利点 | 情報が少ない段階でも、試行錯誤を通して学習し、徐々に最適な選択に近づいていくことができる。新しい選択肢にも柔軟に対応可能。 | 新商品追加時にも素早く人気商品を見つけることができる。 |
ジレンマの解決

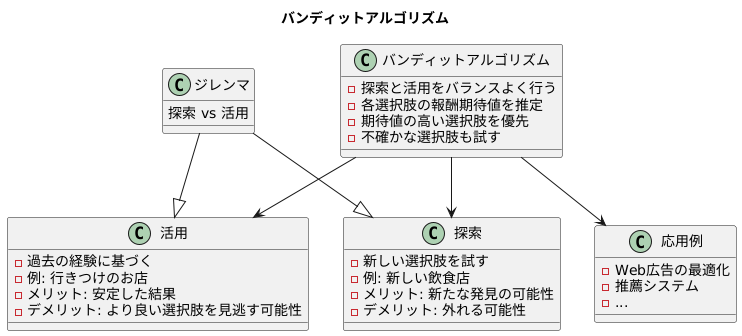
人生においても、仕事においても、様々な場面で選択を迫られることがあります。目の前の利益を追求するか、それとも将来の可能性に賭けるか。これはまさに「探索」と「活用」のジレンマです。例えば、新しい飲食店を開拓するか、それともいつもの行きつけのお店に行くか。新しい店は当たりかもしれないが、外れる可能性もあります。行きつけのお店は安定の味ですが、もっと美味しいお店があるかもしれません。
このジレンマを解決するのが、バンディットアルゴリズムという考え方です。バンディットアルゴリズムは、まるでスロットマシンを扱うかのように、様々な選択肢を試しながら、最適な選択肢を見つけ出します。一つ一つの選択肢をスロットマシンのアームと考え、それぞれのアームを引くことで報酬(飲食店の例では満足度)を得ます。アルゴリズムは、どのアームを引けば最も高い報酬を得られるかを、試行錯誤を通じて学習していきます。
探索は、まだあまり試していないアームを引くことです。新しい飲食店を開拓する行為に相当します。活用は、これまでの経験から最も高い報酬を得られたアームを引くことです。行きつけのお店に行く行為に相当します。バンディットアルゴリズムは、探索と活用をバランスよく行うことで、目先の利益と将来の可能性の両方を追求します。
具体的には、アルゴリズムは、それぞれのアームの報酬の期待値を推定します。そして、期待値が高いアームを優先的に引きますが、同時に、期待値が不確かなアームも試していきます。このように、既知の情報を活かしつつ、未知の情報も積極的に取り入れることで、最適な選択肢にたどり着くのです。このアルゴリズムは、web広告の最適化や推薦システムなど、様々な分野で活用されています。
多様な種類

盗賊退治問題を解くための様々な方法は、それぞれ異なる特性と利点を持っています。状況に応じて最適な方法を選ぶことが重要となります。ここでは代表的な方法をいくつか紹介します。
まず、いつでも最良と思われる行動を選ぶ代わりに、たまに気まぐれで別の行動を試してみる方法があります。これは「気まぐれ選択方法」と呼ばれ、一定の割合で無作為に選択肢を選びます。この割合は、事前に決めておく必要があります。残りの割合では、これまでの経験から最も良い結果をもたらした選択肢を選びます。この方法は、単純で実装しやすいという利点があります。
次に、各選択肢の将来性を見積もり、最も有望な選択肢を選ぶ方法があります。「上限信頼区間(UCB)方法」と呼ばれるこの方法は、それぞれの選択肢がどれだけの成果を上げそうか、そしてまだ試行回数が少ないためにどれだけの不確実性があるのかを計算します。そして、成果の見積もりと不確実性を足し合わせた値が最も高い選択肢を選びます。この方法は、未知の選択肢を積極的に試すことで、より良い選択肢を早く見つける可能性を高めます。
最後に、各選択肢がどれだけの成果を上げそうかを確率的に推定し、その推定に基づいて選択肢を選ぶ方法があります。「確率分布推定サンプリング(トムソンサンプリング)方法」と呼ばれるこの方法は、それぞれの選択肢がどのくらいの確率で成果を上げるかを推定します。そして、その推定に基づいて無作為に選択肢を選びます。この方法は、各選択肢の不確実性をより精密に扱うことができ、結果としてより良い選択肢を見つけ出す可能性を高めます。
このように、盗賊退治問題を解くための方法は様々です。どの方法を選ぶかは、問題の性質や状況によって異なります。それぞれの方法の特性を理解し、適切な方法を選択することが重要です。
| 方法名 | 説明 | 利点 |
|---|---|---|
| 気まぐれ選択方法 | 一定の割合で無作為に選択肢を選び、残りの割合で最も良い結果をもたらした選択肢を選ぶ。 | 単純で実装しやすい。 |
| 上限信頼区間(UCB)方法 | 各選択肢の成果の見積もりと不確実性を足し合わせた値が最も高い選択肢を選ぶ。 | 未知の選択肢を積極的に試すことで、より良い選択肢を早く見つける可能性を高める。 |
| 確率分布推定サンプリング(トムソンサンプリング)方法 | 各選択肢が成果を上げる確率を推定し、その推定に基づいて無作為に選択肢を選ぶ。 | 各選択肢の不確実性をより精密に扱うことができ、結果としてより良い選択肢を見つけ出す可能性を高める。 |
応用事例

探求と活用のバランスをうまくとることで知られるバンディット手法は、様々な場面で活用されています。インターネット上の広告表示はその代表例です。ウェブサイトに複数の広告を掲載する場合、どの広告が最も効果的かはすぐにはわかりません。そこで、バンディット手法を用いることで、表示する広告の種類と頻度を調整しながら、ウェブサイト全体の広告効果を高めることができます。具体的には、最初は様々な広告を均等に表示し、どの広告がクリックされるかなどの反応を調べます。クリック率の高い広告が見つかれば、その広告の表示回数を増やし、クリック率の低い広告の表示回数を減らしていきます。このように、データに基づいてリアルタイムに調整を行うことで、全体的なクリック率の向上を目指します。
また、ニュースサイトの記事推薦にもバンディット手法は応用されています。利用者の過去の閲覧履歴を分析し、それぞれの利用者がどんな記事に興味を持っているかを推測します。そして、興味を持ちそうな記事を優先的に表示することで、利用者の満足度を高めることができます。しかし、過去のデータだけに頼ると、利用者がまだ知らない新しい分野の記事が表示されなくなってしまいます。そこで、バンディット手法を用いて、時々意外性のある記事も表示することで、利用者の視野を広げる機会を提供します。これにより、利用者は新しい情報との出会いを楽しみ、サイトへの関心をさらに高めることができます。このように、バンディット手法は限られた情報から最適な選択を見つけ出し、様々なサービス向上に役立っています。
| 活用場面 | 目的 | 手法 |
|---|---|---|
| インターネット広告 | ウェブサイト全体の広告効果向上(クリック率向上) |
|
| ニュースサイトの記事推薦 | 利用者の満足度向上、視野拡大 |
|
今後の展望

これまで見てきたように、バンディットアルゴリズムは様々な場面で役立つ意思決定の方法であり、今後ますますその重要性を増していくと考えられます。人工知能の研究においても、バンディットアルゴリズムは中心的な役割を担っており、機械学習や深層学習といった他の手法と組み合わせられることで、さらに強力な道具となるでしょう。
たとえば、機械学習を用いて大量の情報を処理し、その結果に基づいてバンディットアルゴリズムが最適な行動を選び出すといった連携が考えられます。深層学習との組み合わせも、複雑な状況における意思決定を可能にする革新的な技術となる可能性を秘めています。これらの技術が融合することで、より高度な判断や予測が可能になり、様々な分野で応用されることが期待されます。
特に注目すべきは、一人ひとりに合わせたサービスを提供する技術、いわゆる個人最適化への応用です。インターネット広告や商品の推奨など、利用者の行動や好みに合わせて最適な選択肢を提示する場面で、バンディットアルゴリズムは既に活用されています。今後、この分野はますます発展し、個々の利用者に最適化された医療、教育、金融サービスなど、私たちの生活の様々な側面で、より良い選択をするための手助けとなるでしょう。
さらに、バンディットアルゴリズムは、資源の効率的な利用にも貢献すると期待されています。限られた資源をどのように分配するか、という問題は、社会全体にとって重要な課題です。バンディットアルゴリズムを用いることで、試行錯誤を通じて最適な資源配分を見つけ出し、無駄を省きつつ最大の効果を得ることが可能になります。エネルギー管理、交通制御、災害対策など、様々な分野でその活用が期待され、私たちの社会をより良くしていく力となるでしょう。このように、バンディットアルゴリズムは今後ますます発展し、私たちの生活をより豊かに、より便利にしていく可能性を秘めた、大変重要な技術と言えるでしょう。
| 分野 | バンディットアルゴリズムの応用 | 期待される効果 |
|---|---|---|
| 人工知能 | 機械学習や深層学習との組み合わせ | より高度な判断や予測 |
| 個人最適化 | インターネット広告、商品の推奨、医療、教育、金融サービス | 利用者に最適化されたサービス提供 |
| 資源の効率的利用 | エネルギー管理、交通制御、災害対策 | 無駄を省きつつ最大の効果 |
まとめ

限られた情報から最良の選択を見つけ出す、まるで宝探しのような手法、それがバンディットアルゴリズムです。この手法は、宝探しの冒険家が未知の洞窟を探検するように、「探索」と「活用」のバランスをうまくとることで、最良の選択へと私たちを導いてくれます。
たとえば、ウェブサイトで商品をおすすめしてくれる機能を考えてみましょう。サイト運営者は、どの商品をユーザーにおすすめすれば、より多く買ってもらえるかを知りたいと思っています。しかし、どの商品が人気なのかは、実際に試してみないとわかりません。そこで、バンディットアルゴリズムの出番です。アルゴリズムは、まだあまり表示されていない商品をユーザーに「探索」的に表示してみます。そして、ユーザーがその商品をクリックしたり、購入したりする反応を見て、その商品の「価値」を評価します。同時に、既に人気があるとわかっている商品は積極的にユーザーに「活用」的に表示します。このように、探索と活用を繰り返すことで、アルゴリズムは次第にどの商品が最も効果的かを学習し、ユーザーにとって最適な商品を表示できるようになるのです。
この賢いアルゴリズムは、すでに様々な場面で活躍しています。ウェブサイトでの広告配信はもちろん、ニュース記事の推薦、さらには医療分野での治療方針の決定など、データに基づいて最適な選択を行う必要がある場面で広く利用されています。人工知能技術の進歩とともに、バンディットアルゴリズムはますます進化を遂げ、より複雑な状況にも対応できるようになっています。近い将来、私たちの生活の様々な場面で、このアルゴリズムがより高度な意思決定を支え、より豊かな社会を実現する鍵となるでしょう。今後の進化と応用から、ますます目が離せません。
| 手法 | 特徴 | 例 | 応用分野 |
|---|---|---|---|
| バンディットアルゴリズム | 限られた情報から最良の選択を見つけ出す。「探索」と「活用」のバランスをとる。 | ウェブサイトでの商品推薦:
|
|
