勾配降下法の進化:最適化手法

AIを知りたい
先生、勾配降下法の弱点と、それを改善する方法について教えてください。

AIエンジニア
勾配降下法は、一番誤差が小さくなる重みを探すのに、傾きを使って探していく方法だね。でも、時間がかかったり、一番良い答えじゃなくて、まあまあの答えで満足してしまうことがあるんだ。これを改善する方法として、『勢い』を使う方法と、『だんだん小さくする』方法があるよ。

AIを知りたい
『勢い』を使う方法と『だんだん小さくする』方法とは、具体的にどういうことですか?

AIエンジニア
『勢い』を使う方法は、傾きの大きさによって更新する量を変えることで、まあまあの答えで満足しにくくする方法だよ。一方、『だんだん小さくする』方法は、最初は大きく学習して、だんだん小さくしていくことで、効率よく学習を進める方法なんだ。この二つの良いところどりをしたのが、『アダム』という方法で、色々な場面で使われているんだよ。
勾配降下法の問題と改善とは。
人工知能でよく使われる「勾配降下法」には、問題点があります。勾配降下法とは、誤差を少なくするために最適な値を探す方法ですが、時間がかかりすぎたり、本当に一番良い値ではなく、その場限りの良い値に落ち着いてしまうことがあります。これを解決するために、「モメンタム」や「エイダグラッド」といった方法があります。モメンタムは、誤差の大きさによって値の更新の度合いを変えることで、その場限りの良い値に落ち着く可能性を減らします。エイダグラッドは、最初は学習の速さを大きくし、徐々に小さくしていくことで、効率的に学習を進めます。さらに、この二つの考え方を組み合わせた「アダム」という方法があり、幅広く使われています。
勾配降下法:基本と課題

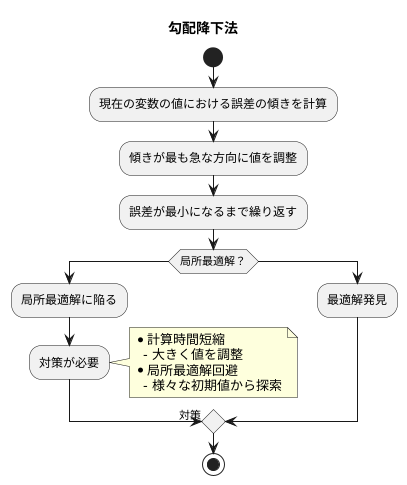
勾配降下法は、機械学習の分野で、最適な変数の値を見つけるための基本的な方法です。この方法は、山を下ることに例えられます。山の斜面は、変数の値によって変わる誤差の大きさを表していて、目標は、誤差が最も小さくなる谷底を見つけることです。
具体的には、現在の変数の値における誤差の傾きを計算します。この傾きは、誤差がどのくらい急激に変化するかを示しています。そして、この傾きが最も急な方向に、変数の値を少しずつ調整します。まるで山の斜面を少しずつ下っていくように、この調整を何度も繰り返すことで、最終的には誤差が最も小さくなる谷底にたどり着くことを目指します。
しかし、この方法にはいくつか難しい点もあります。一つは、計算に時間がかかることです。特に扱う情報が多い場合、谷底にたどり着くまでに膨大な計算が必要になり、時間がかかってしまうことがあります。もう一つは、局所最適解と呼ばれる、浅い谷に捕らわれてしまう可能性があることです。山には複数の谷がある場合、最も深い谷底ではなく、近くの浅い谷で探索が終わってしまうことがあります。この浅い谷は、全体で見れば最適な場所ではないため、真に最適な変数の値を見つけることができません。ちょうど、登山家が深い谷を目指していたのに、途中の小さな谷で満足してしまい、真の目的地にたどり着けない状況に似ています。そのため、勾配降下法を使う際には、これらの課題を理解し、適切な対策を講じることが重要です。例えば、計算時間を短縮するために、一度に大きく値を調整するといった工夫や、局所最適解に陥らないように、様々な初期値から探索を始めるといった工夫が考えられます。
モメンタム:慣性を利用

勾配降下法は、機械学習において広く使われている最適化手法ですが、いくつかの課題も抱えています。例えば、複雑な関数においては、浅い谷に捕まり、最適な解にたどり着けない「局所最適解」の問題や、学習の進行が遅いといった点が挙げられます。これらの課題を解決するために、様々な改良手法が開発されてきました。その一つが、物理の慣性の概念を取り入れた「モメンタム」です。
勾配降下法では、各段階で関数の傾きが最も急な方向へとパラメータを調整します。まるで山の斜面を下るように、一歩一歩、谷底を目指して進んでいくイメージです。しかし、この方法では、小さな谷に落ち込んでしまうと、そこから抜け出すのが難しくなります。
モメンタムは、この問題を解決するために、過去の調整量を「慣性」として利用します。これは、ボールが斜面を転がる様子を想像すると分かりやすいでしょう。ボールは、現在の斜面の傾きだけでなく、過去の運動量も影響を受けて進みます。そのため、小さな谷に落ち込んでも、過去の勢いによって谷を乗り越え、より深い谷底へと進むことができます。
モメンタムは、局所最適解を回避するだけでなく、学習速度の向上にも貢献します。関数の傾きが一定の方向を向いている場合、過去の調整量が積み重なることで、より大きな一歩でパラメータを調整できます。これは、平坦な道を進む際に、速度を上げて移動する様子に似ています。結果として、最適な解にたどり着くまでの時間を短縮することができるのです。
このように、モメンタムは慣性の概念を利用することで、勾配降下法の課題を効果的に克服し、より効率的な学習を実現する手法と言えるでしょう。
適応型学習率:AdaGrad

学習をより効率的に行うために、様々な工夫が凝らされています。その一つが、AdaGrad(適応勾配アルゴリズム)と呼ばれる学習率の調整方法です。
機械学習では、パラメータと呼ばれる値を繰り返し調整することで、予測の精度を高めていきます。この調整を行う際に、一度にどの程度値を変化させるかを決めるのが学習率です。
AdaGradは、それぞれのパラメータに対して、過去の変化量に基づいて学習率を個別に調整します。具体的には、これまでパラメータがどれだけ変化してきたかを記録し、変化量の二乗和を計算します。そして、この二乗和が大きいパラメータほど、学習率を小さく設定します。
これは、頻繁に更新されてきたパラメータは、すでに最適な値に近づいている可能性が高いという考え方に基づいています。そのため、小さな学習率で慎重に調整することで、最適な値を通り過ぎてしまうことを防ぎます。
逆に、あまり更新されていないパラメータは、まだ最適な値から遠い可能性が高いとされます。このようなパラメータには、大きな学習率を設定することで、最適な値へと迅速に近づけることができます。
このように、AdaGradはそれぞれのパラメータに適した学習率を用いることで、学習の効率を高める手法と言えるでしょう。パラメータの更新履歴を活用することで、より精度の高い予測モデルを構築することが期待できます。
| 手法 | 説明 | 利点 |
|---|---|---|
| AdaGrad (適応勾配アルゴリズム) | パラメータごとに過去の変化量に基づいて学習率を調整する。変化量の二乗和が大きいパラメータほど学習率を小さくする。 | 学習の効率を高め、より精度の高い予測モデルを構築できる。頻繁に更新されたパラメータは最適値に近づいているため学習率を小さくし、更新が少ないパラメータは最適値から遠いため学習率を大きくすることで、それぞれのパラメータに適した学習率を設定できる。 |
Adam:二つの利点を融合

学習の効率を高める手法として、様々な方法が研究されていますが、その中で現在最も広く使われている手法の一つがAdam(適合的な積率推定)です。これは、これまでの勾配降下法の改良型で、二つのすぐれた手法、運動量法とAdaGradそれぞれの利点を組み合わせたものです。
まず、運動量法に着目してみましょう。運動量法は、過去の更新量を考慮することで、勾配の振動を抑え、谷間のような狭い局所最適解に陥らず、より良い解を見つけやすくする効果があります。まるでボールが坂を転がり落ちるように、過去の運動量の勢いを保ちながら最適解へと進んでいくイメージです。
次に、AdaGradについて見ていきましょう。AdaGradは、パラメータごとに学習率を調整する手法です。これにより、更新頻度の少ないパラメータは大きく更新し、更新頻度の高いパラメータは小さく更新することで、学習の効率を高めます。
Adamはこの二つの手法の利点をうまく組み合わせることで、より速く、より確実に最適解へと近づくことができます。具体的には、過去の勾配の一次積率(平均)と二次積率(分散)をそれぞれ推定し、それらを用いてパラメータの更新量を調整します。一次積率は運動量法のように過去の勾配の影響を考慮し、二次積率はAdaGradのようにパラメータごとの学習率を調整する役割を果たします。
このような特性から、Adamは多くの機械学習の計算手順集に組み込まれており、様々な課題に対して高い性能を示すことが知られています。特に、多くの層を持つ複雑なモデルである深層学習においても、Adamは効率的かつ効果的な最適化を実現する強力な手法として活用されています。画像認識や自然言語処理など、様々な分野でAdamは学習を支える重要な役割を担っています。
手法選択の重要性

機械学習において、目的を達成するためには様々な手法が存在しますが、どの手法を選ぶかが結果に大きく影響します。特に、勾配降下法を改良した手法はそれぞれ異なる特性を持つため、問題の性質やデータの特徴に合わせて適切なものを選ばなければなりません。
例えば、扱うデータの次元数が多い場合を考えてみましょう。AdaGradは過去の勾配の二乗和の平方根で学習率を調整するため、高次元データでは学習の初期段階で学習率が急速に小さくなり、学習が停滞することがあります。これは、各次元に対して個別に学習率が調整されるため、次元数が増えると調整が過剰になるためです。
一方、モメンタムは過去の勾配の情報を蓄積し、慣性のように学習を進めるため、高次元データに対しても比較的安定した性能を示します。これは、過去の勾配の方向を考慮することで、局所的な最適解に陥りにくくなるためです。
Adamは、モメンタムとAdaGradの両方の利点を組み合わせた手法です。過去の勾配の情報を用いることで、モメンタムのように安定した学習を実現しつつ、AdaGradのように各パラメータに対して適切な学習率を調整します。そのため、多くの問題において優れた性能を発揮します。
しかし、Adamが常に最適な手法であるとは限りません。問題によっては、他の手法がより適している場合もあります。例えば、データの特性やモデルの複雑さによっては、RMSpropやNesterov加速勾配降下法など、他の改良手法がAdamよりも優れた結果を出すことがあります。
最適な手法を選ぶためには、様々な手法を試してみて、実際に性能を比較することが重要です。さらに、各手法には調整可能なパラメータが存在します。これらのパラメータを調整することで、手法の性能をさらに向上させることができます。
適切な手法とパラメータを選ぶことは、機械学習モデルの学習効率を向上させ、精度の高いモデルを構築するために不可欠です。時間をかけて様々な手法とパラメータを試すことで、最終的に望ましい結果を得ることができるでしょう。
| 手法 | 特徴 | 長所 | 短所 | 適する状況 |
|---|---|---|---|---|
| AdaGrad | 過去の勾配の二乗和の平方根で学習率を調整 | 各パラメータに適した学習率調整 | 高次元データで学習率が急速に低下、学習停滞の可能性 | 低次元データ |
| モメンタム | 過去の勾配の情報を蓄積、慣性のように学習 | 高次元データでも安定した性能、局所最適解に陥りにくい | – | 高次元データ |
| Adam | モメンタムとAdaGradの利点を組み合わせ | 安定した学習と各パラメータへの適切な学習率調整、多くの問題で優れた性能 | 常に最適とは限らない | 多くの問題 |
| RMSprop | – | Adamより優れる場合も | – | データ特性やモデルの複雑さによる |
| Nesterov加速勾配降下法 | – | Adamより優れる場合も | – | データ特性やモデルの複雑さによる |
