深層学習で学ぶ強化学習:DQN入門

AIを知りたい
先生、DQNの説明でQテーブルを更新していくってありましたが、具体的にどういうことですか?

AIエンジニア
いい質問だね。例えば、スタート地点Aからゴール地点Iに行くことを考えると、AからBに移動するとゴールに近づくから報酬は+1だね。このとき、QテーブルのAからBへの行動の価値が、計算式によって更新されるんだ。具体的には、現在の状態の報酬と、次の状態での最も高いQ値に割引率をかけた値を足し合わせたものになる。

AIを知りたい
なるほど。でも、割引率ってなんですか?

AIエンジニア
割引率は、将来の報酬をどれくらい重要視するかを決める値だよ。例えば、割引率が小さいと、今すぐもらえる報酬を重視するようになる。逆に割引率が大きいと、将来もらえる報酬も今と同じくらい重要視するようになるんだ。
DQNとは。
ディープマインド社が発表した、人工知能の強化学習の方法の一つである「DQN」について説明します。まず、始点をA、終点をIとした道筋を考えてみましょう。ゴールに近づく行動にはプラス1点、遠ざかる行動にはマイナス1点、ゴールに辿り着いたらプラス100点といったように、行動の結果に対する点数を設定します。そして、それぞれの状況と行動に対する点数を記録する「Qテーブル」を用意します。Qテーブルの最初の値は全て0です。DQNはこのQテーブルの値を繰り返し更新することで学習を進めます。テーブルの中の値が大きいほど、良い行動だと判断するわけです。Qテーブルの値は、計算式を使って更新されます。この式の中には「割引率」と呼ばれる値が含まれていて、行動の回数が増えるほど、その行動の価値を低く評価するように調整する役割を果たします。
はじめに

近頃、様々な機械に知恵を与える技術である人工知能は、目覚ましい発展を遂げています。この技術の中でも、強化学習と呼ばれる方法は特に注目を集めており、様々な分野で応用が始まっています。強化学習とは、まるで人間が学習するように、試行錯誤を繰り返しながら、目的とする行動を身につける方法です。
例えば、未知のゲームに挑戦する場面を考えてみましょう。最初は遊び方が全く分からなくても、何度も遊ぶうちに、高い得点を得るための戦略を自然と学ぶことができます。強化学習もこれと同じように、最初は何も知らない状態から、成功と失敗を繰り返すことで、最適な行動を見つけ出していきます。この学習方法は、ロボットの動きを制御したり、複雑なゲームを攻略したり、自動運転技術を向上させるなど、幅広い分野で役立っています。
この強化学習の中でも、深層学習と組み合わせた深層強化学習という方法が、近年大きな成果を上げています。深層強化学習は、人間の脳の仕組みを模倣した深層学習を用いることで、より複雑な状況にも対応できるようになりました。その代表例が、今回紹介する「深層Q学習網(DQN)」と呼ばれる手法です。「Q学習網」とは、将来得られるであろう価値を予測しながら学習を進める方法です。ここに深層学習を組み合わせたDQNは、従来の方法では難しかった高度な問題解決を可能にしました。
DQNは、囲碁や将棋といったゲームで人間を上回る強さを示した人工知能の開発にも貢献しており、人工知能の発展に大きく貢献しました。この技術は、今後さらに様々な分野で応用されていくことが期待されています。
| 項目 | 説明 |
|---|---|
| 人工知能 | 様々な機械に知恵を与える技術 |
| 強化学習 | 試行錯誤を繰り返しながら、目的とする行動を身につける学習方法 |
| 深層強化学習 | 深層学習と強化学習を組み合わせた学習方法。より複雑な状況に対応可能。 |
| 深層Q学習網(DQN) | 将来得られるであろう価値を予測しながら学習するQ学習網に深層学習を組み合わせた手法。高度な問題解決が可能。 |
| 応用例 | ロボットの制御、複雑なゲーム攻略、自動運転技術向上、囲碁・将棋AIなど |
経路探索問題

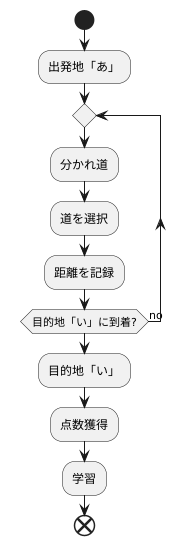
道順を見つける問題は、私たちの日常生活でもよく出会うものです。例えば、初めて訪れる場所への行き方を調べたり、渋滞を避けるための抜け道を考えたりする時などがそうです。ここでは、人工知能の学習方法の一つである、深い確報学習という手法を学ぶために、簡単な道探しを例に考えてみましょう。出発地から目的地までの最短ルートを見つけることが目的です。
出発地を「あ」、目的地を「い」とします。「あ」から「い」までは、いくつかの分かれ道を通る必要があります。それぞれの分かれ道で、どの道を選ぶかによって、目的地までの距離が変わってきます。深い確報学習は、この道探しを、何度も試行錯誤を繰り返しながら最適なルートを学習するという方法で解決します。
はじめは、行き当たりばったりに道を選びます。まるで迷路の中で、手探りで出口を探しているようなものです。そして、目的地に着くまでにどの道を通ったのか、また、その道のりがどれくらいだったのかを記録します。この記録をもとに、どの分かれ道でどの道を選べば目的地に早く着けるのかを学習していきます。
目的地に早く着くほど高い点数がもらえるように設定しておきます。まるでゲームのスコアのように、より良い選択をするほど高い点数が得られる仕組みです。深い確報学習は、この点数を最大にするように、つまり、より短いルートを見つけられるように、分かれ道での道の選び方を学習していくのです。あたかも、何度も迷路に挑戦することで、最短ルートを覚えていくかのようです。このように、深い確報学習は、試行錯誤と学習を繰り返すことで、複雑な問題を解決する方法を自ら見つけていくことができるのです。
報酬とQテーブル

強化学習という考え方の基では、何かを学ぶために、良し悪しを数値で示す必要があります。この良し悪しを表す数値を、報酬といいます。たとえば、迷路の例を考えてみましょう。迷路の出口にたどり着くことが目的であれば、出口に近づく行動にはプラスの報酬を与えます。反対に、出口から遠ざかる行動や、壁にぶつかる行動にはマイナスの報酬を与えます。
このように行動の良し悪しを報酬で表すことで、どの行動が良いかを学習していきます。しかし、迷路のように複雑な課題では、単純に行動の良し悪しだけでなく、将来にわたって得られる報酬の合計も考える必要があります。たとえば、今は遠回りでも、最終的に出口にたどり着く道を選ぶ方が良い場合があります。
そこで登場するのが「Qテーブル」です。Qテーブルとは、それぞれの場所で、どのような行動をとれば、最終的にどれだけの報酬が得られるかを表にしたものです。迷路の例で言えば、各分岐点で、どの道を選ぶべきかを判断するための情報がQテーブルに記録されています。
Qテーブルの各項目には、状態と行動の組み合わせに対する、将来得られる報酬の期待値が格納されています。具体的には、ある場所で特定の行動をとった場合に、最終的に得られると期待される報酬の合計が記録されています。この値が大きいほど、その場所でその行動をとることが良いと判断されます。
学習の過程では、試行錯誤を繰り返しながら、実際の行動で得られた報酬に基づいて、Qテーブルの値を更新していきます。最初はランダムな行動をとりながら、得られた報酬をもとにQテーブルを修正していきます。学習が進むにつれて、Qテーブルの値はより正確になり、最適な行動を選択できるようになっていきます。このように、報酬とQテーブルは強化学習において重要な役割を果たしています。
| 用語 | 説明 |
|---|---|
| 報酬 | 行動の良し悪しを表す数値。出口に近づく行動にはプラス、遠ざかる行動にはマイナスの報酬を与える。 |
| Qテーブル | 各場所でどのような行動をとれば最終的にどれだけの報酬が得られるかを表にしたもの。各項目には、状態と行動の組み合わせに対する将来得られる報酬の期待値が格納されている。 |
| 学習過程 | 試行錯誤を繰り返しながら、実際の行動で得られた報酬に基づいてQテーブルの値を更新していく。最初はランダムな行動をとり、学習が進むにつれてQテーブルの値はより正確になり、最適な行動を選択できるようになる。 |
Q値の更新

行動の価値を学習する手法である「Q学習」では、行動の良し悪しを数値で表す「Q値」を用います。このQ値は、ある状態である特定の行動をとった場合の将来得られる報酬の期待値を表しており、Q値の更新によって学習を進めていきます。
Q値の更新は、数式に基づいて行われます。この数式は、現在の状態における行動で得られる報酬と、次の状態における最も良い行動をとった場合のQ値、そして「割引率」と呼ばれる値から成り立っています。
現在の状態での報酬は、まさにその場で得られる直接的なものです。例えば、迷路でゴールに到達すれば高い報酬が得られ、落とし穴に落ちれば低い報酬が得られる、といった具合です。
次の状態における最も良い行動をとった場合のQ値は、将来得られるであろう報酬の期待値です。迷路の例で言えば、次のマスに移動した際に、そこからゴールまでの道筋で得られるであろう報酬の期待値を意味します。
割引率は、将来の報酬をどのくらい重視するかを調整する値です。割引率の値は、0から1の間で設定されます。割引率が小さい場合は、将来の報酬をあまり重視せず、目先の報酬を優先するようになります。逆に、割引率が大きい場合は、将来の報酬を重視し、長期的に見てより多くの報酬を得られる行動を選択するようになります。
この更新の式を何度も繰り返し適用することで、Q値は徐々に最適な値に近づいていきます。つまり、各状態においてどの行動をとるのが最も良いのかを学習していくのです。そして最終的には、どの状態からでも最も報酬が得られる行動の組み合わせ、すなわち最適な行動方針を導き出すことができるようになります。
| 項目 | 説明 |
|---|---|
| Q学習 | 行動の価値を学習する手法 |
| Q値 | 行動の良し悪しを表す数値。ある状態である特定の行動をとった場合の将来得られる報酬の期待値 |
| Q値の更新 | 現在の状態における行動で得られる報酬、次の状態における最も良い行動をとった場合のQ値、割引率を用いて計算 |
| 現在の状態での報酬 | その場で得られる直接的な報酬 |
| 次の状態における最も良い行動をとった場合のQ値 | 将来得られるであろう報酬の期待値 |
| 割引率 | 将来の報酬をどのくらい重視するかを調整する値 (0~1) |
| 割引率が小さい場合 | 将来の報酬をあまり重視せず、目先の報酬を優先 |
| 割引率が大きい場合 | 将来の報酬を重視し、長期的に見てより多くの報酬を得られる行動を選択 |
| Q値の更新の繰り返し | Q値を最適な値に近づけ、各状態においてどの行動をとるのが最も良いのかを学習 |
| 学習結果 | どの状態からでも最も報酬が得られる行動の組み合わせ(最適な行動方針)を導き出す |
深層学習の活用

深層学習は、人間の脳の仕組みを模倣した技術であり、近年様々な分野で目覚ましい成果を上げています。特に、深層学習と強化学習を組み合わせた手法は、複雑な問題を解決する上で非常に強力な道具となっています。その代表例が、DQN(深層Q学習)です。従来の強化学習では、Qテーブルと呼ばれる表を用いて、状態と行動の組み合わせに対する価値(Q値)を記録していました。しかし、この方法は状態や行動の種類が増えると、テーブルのサイズが爆発的に大きくなり、扱いが困難になるという問題を抱えていました。
DQNは、この問題を解決するために、Qテーブルの代わりに深層学習モデルを使うという革新的なアイデアを採用しました。この深層学習モデルは、現在の状態を入力として受け取り、それぞれの行動に対するQ値を出力します。つまり、膨大な数の状態と行動の組み合わせを、コンパクトなモデルで表現できるようになったのです。これにより、従来の方法では不可能だった、複雑な状態を持つ問題にも対応できるようになりました。
DQNは、ゲームの分野で大きな成功を収めました。例えば、ブロック崩しやパックマンといった古典的なゲームにおいて、人間を凌駕するスコアを叩き出しました。さらに、囲碁や将棋といった複雑なゲームでも、深層学習を取り入れたAIがプロ棋士に勝利するなど、目覚ましい成果を上げています。
DQNの応用範囲はゲームにとどまりません。ロボット制御の分野では、DQNを用いてロボットに複雑な動作を学習させる試みが盛んに行われています。また、自動運転技術の開発においても、DQNは重要な役割を担っています。周囲の状況を認識し、安全かつ効率的な運転を学習させることで、自動運転の実現に大きく貢献することが期待されています。このように、DQNは様々な分野で革新をもたらしており、今後も更なる発展が期待される技術です。
| 項目 | 説明 |
|---|---|
| 深層学習 | 人間の脳の仕組みを模倣した技術 |
| 強化学習 | 深層学習と組み合わせることで、複雑な問題解決に強力な道具となる |
| DQN (深層Q学習) | 深層学習と強化学習を組み合わせた手法。Qテーブルの代わりに深層学習モデルを使用 |
| Qテーブル | 従来の強化学習で使用。状態と行動の組み合わせに対する価値(Q値)を記録 |
| Qテーブルの問題点 | 状態や行動の種類が増えるとテーブルサイズが爆発的に大きくなり、扱いが困難 |
| DQNの利点 | 膨大な状態と行動の組み合わせをコンパクトなモデルで表現可能 |
| DQNの適用分野 | ゲーム(ブロック崩し、パックマン、囲碁、将棋)、ロボット制御、自動運転 |
今後の展望

深層強化学習の手法の一つである深層Q学習網(DQN)は、人工知能(AI)の発展に大きく貢献しました。ゲームの攻略や自動運転など、これまで難しいと考えられていた制御の難題を次々と解決できる可能性を示し、この分野に大きな進歩をもたらしたのです。しかし、DQNは完璧ではなく、いまだにいくつかの課題を抱えています。
まず、学習の安定性が課題として挙げられます。DQNは、試行錯誤を通じて学習を進めますが、この学習過程は必ずしも順調ではありません。時には学習が不安定になり、なかなか性能が向上しない場合もあります。また、学習の効率性も重要な課題です。複雑な問題を解くためには膨大な量のデータと計算時間が必要となる場合があり、より効率的な学習手法の開発が求められています。さらに、探索と活用のバランスも難しい問題です。AIは、既知の情報に基づいて行動を選択する活用と、未知の情報を得るための探索を適切に組み合わせる必要がありますが、このバランスをうまくとることが難しいのです。
しかし、これらの課題を克服するために、DQNを改良する様々な研究が進められています。例えば、学習の安定性を高めるための手法や、学習効率を向上させるためのアルゴリズムなどが提案されています。また、探索と活用のバランスを最適化する手法も研究されています。これらの改良により、DQNは今後さらに発展し、より複雑で難しい問題を解決できるようになると期待されています。
DQNの応用範囲も広がりつつあります。ゲームや自動運転だけでなく、医療や金融、製造業など、様々な分野での応用が期待されています。例えば、病気の診断支援や投資戦略の最適化、工場の生産工程の効率化など、DQNは私たちの生活に役立つ様々なAIシステムの開発に貢献する可能性を秘めているのです。今後の研究により、DQNの性能が向上し、応用範囲がさらに広がることで、私たちの生活はより豊かになるでしょう。
| 項目 | 内容 |
|---|---|
| 手法名 | 深層Q学習網(DQN) |
| 貢献 | 人工知能(AI)の発展に大きく貢献、ゲーム攻略や自動運転など制御の難題解決 |
| 課題 | 学習の安定性、学習の効率性、探索と活用のバランス |
| 課題への対策 | 学習安定性向上、学習効率向上アルゴリズム、探索活用バランス最適化手法 |
| 応用範囲 | ゲーム、自動運転、医療、金融、製造業など |
| 応用例 | 病気の診断支援、投資戦略の最適化、工場の生産工程の効率化 |
| 将来展望 | 性能向上、応用範囲拡大による生活の向上 |
