t-SNEでデータの可視化

AIを知りたい
先生、「t-SNE」って次元削減の手法の一つだってことはわかったんですけど、普通の次元削減と何が違うんですか?

AIエンジニア
いい質問だね。t-SNEは、データの「密集度」をなるべく保ったまま次元を下げることを得意としているんだ。たとえば、高次元空間でいくつかのまとまりに分かれているデータを二次元に落とすことを考えてみよう。普通の方法だと、それぞれのまとまりが重なってしまって区別がつかなくなることもある。でも、t-SNEは、それぞれのまとまりがなるべく重ならないように二次元上に配置してくれるんだ。

AIを知りたい
なるほど。つまり、データの「似たもの同士は近く、そうでないものは遠く」を保ちながら次元を下げるってことですね?

AIエンジニア
その通り!より正確に言うと、高次元でのデータの近さを確率で表し、低次元でも同じように確率で表して、その二つの確率分布がなるべく近くなるように次元削減を行うんだ。この確率分布の近さを測るのに使われているのがKLダイバージェンスという指標だよ。
t-SNEとは。
『t-SNE』というAI用語について説明します。t-SNEとは、t-distributed stochastic neighbor embeddingの略で、SNEを改良した次元削減手法です。次元削減とは、たくさんのデータの特徴をできるだけ損なわずに、少ない情報で表現する手法のことです。t-SNEでは、まずもとのデータで、二つのデータの近さを確率で表します。次に、次元を減らした後のデータでも、同じように二つのデータの近さを確率で表します。そして、もとのデータでの確率と、次元削減後のデータでの確率の差を、KLダイバージェンスという尺度を使って測ります。この尺度は、二つの確率分布の似ている度合いを表すもので、値が小さいほどよく似ています。t-SNEは、このKLダイバージェンスの値が小さくなるように、つまり、次元削減後もデータ同士の近さがなるべく変わらないように、次元を削減します。
次元削減とは

たくさんの情報を持つデータのことを、高次元データと言います。例えば、ある商品の購入者のデータには、年齢、性別、居住地、年収、趣味など、様々な情報が含まれているとします。これらの情報一つ一つがデータの特徴を表す要素であり、次元と呼ばれるものです。次元が多ければ多いほど、データは多くの情報を持っていることになりますが、同時に処理が複雑になり、全体像を掴むのが難しくなります。まるで、たくさんの道が入り組んだ迷路に入り込んでしまったかのようです。
そこで登場するのが、次元削減という技術です。次元削減とは、データの特徴をなるべく損なわずに、次元の数を減らす技術のことです。迷路の全体像を把握するために、不要な道を少しずつ減らしていく作業に似ています。次元削減を行うことで、データの処理を簡素化し、全体像を容易に把握できるようになります。また、データの中に潜む重要な関係性を見つけやすくなるという利点もあります。
次元削減には様々な方法がありますが、それぞれ得意な分野が異なります。例えば、t-SNEと呼ばれる方法は、データを視覚的に分かりやすく表現することに優れています。高次元データを二次元や三次元に圧縮することで、人間の目で見て理解できる形に変換するのです。まるで、複雑な迷路を上空から見て、全体構造を把握するようなものです。このように、次元削減は、複雑なデータを分析しやすく、理解しやすくするための、強力な道具と言えるでしょう。
t-SNEの仕組み

t-SNE(ティー・スニー)とは、高次元のデータを低次元(主に二次元や三次元)に落とし込み、可視化する手法です。高次元空間にあるデータ点同士の距離関係を維持したまま、低次元空間へ写像することで、データの全体像を把握しやすくなります。
t-SNEの仕組みは、高次元空間におけるデータ点の近さを確率に変換することから始まります。あるデータ点に着目したとき、その点の近くに他のデータ点が存在する確率を計算します。この確率は、高次元空間でのデータ点間の距離に基づいて算出されます。近いデータ点ほど確率は高く、遠いデータ点ほど確率は低くなります。
次に、低次元空間にも同様の確率分布を構築します。高次元空間での確率分布と低次元空間での確率分布ができるだけ一致するように、低次元空間におけるデータ点の配置を調整していきます。この調整は、二つの確率分布間の違いを測る尺度であるKLダイバージェンスを用いて行われます。KLダイバージェンスが小さくなるように、つまり二つの確率分布が似るように、低次元空間のデータ点を移動させていきます。
このように、t-SNEは高次元空間でのデータ点の近さを確率分布として捉え、その確率分布を低次元空間で再現することで次元削減を実現しています。高次元空間で近かったデータ点は低次元空間でも近くに、遠かったデータ点は遠くになるように配置されるため、データの構造を視覚的に把握しやすくなります。ただし、確率に基づいた手法であるため、低次元空間での距離は必ずしも高次元空間での距離を正確に反映しているとは限りません。そのため、t-SNEの結果を解釈する際には注意が必要です。また、計算に時間がかかるという欠点もあります。
| 項目 | 説明 |
|---|---|
| 手法名 | t-SNE (ティー・スニー) |
| 目的 | 高次元データを低次元(主に2次元/3次元)に落とし込み、可視化 |
| 仕組み | 高次元空間のデータ点同士の距離関係を維持したまま低次元空間へ写像 |
| ステップ1 | 高次元空間のデータ点の近さを確率に変換
|
| ステップ2 | 低次元空間にも同様の確率分布を構築
|
| 特徴 | 高次元空間で近かったデータ点は低次元空間でも近くに、遠かったデータ点は遠くに配置
|
SNEからの改良点

SNEを改良して生まれたのが、t-SNEという手法です。この改良によって、データの可視化における課題が解決され、より分かりやすい表現が可能となりました。
SNEでは、高次元空間にあるデータ同士の距離を測るために、確率分布の一つであるガウス分布を利用していました。そして、この高次元空間での距離関係を維持したまま、低次元空間へデータを配置しようとします。低次元空間でのデータ同士の距離は、t分布を使って表現していました。つまり、高次元空間ではガウス分布、低次元空間ではt分布と、異なる確率分布を使う非対称な手法でした。
しかし、この非対称性であるがゆえに、「混雑問題」と呼ばれる現象が生じやすくなりました。これは、低次元空間へ落とし込む際に、データ点が互いに密集し、本来離れているべきデータ点同士がくっついて見えてしまう問題です。たくさんの点がぎゅっと集まってしまい、データの構造が見えにくくなってしまうのです。
t-SNEでは、この混雑問題を解消するために、低次元空間でもt分布を使うようにしました。高次元、低次元空間の両方で同じt分布を使うことで、対称性を保ち、混雑問題を軽減することに成功したのです。t分布はガウス分布に比べて裾野が広く、中心から離れた値も考慮に入れやすい特徴があります。そのため、データ間の距離関係をより適切に表現することができ、高次元空間の構造を低次元空間へより正確に反映できるようになりました。
このように、t-SNEはSNEの弱点を克服し、高次元データをより分かりやすく可視化する、強力な手法として知られています。
| 手法 | 高次元空間の距離 | 低次元空間の距離 | 対称性 | 混雑問題 |
|---|---|---|---|---|
| SNE | ガウス分布 | t分布 | 非対称 | 発生しやすい |
| t-SNE | t分布 | t分布 | 対称 | 軽減 |
可視化の利点

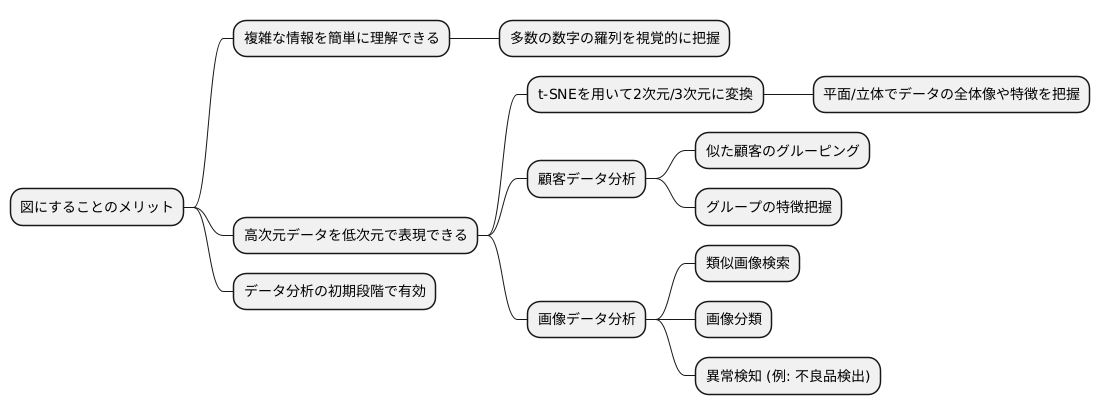
図にすることには多くの良い点があります。たくさんの数字の羅列では全体を掴むのが難しいことがありますが、図にすることで、複雑な情報もすぐに理解できるようになります。
高次元データとは、たくさんの情報が絡み合っているデータのことです。このようなデータはそのままでは理解が難しいのですが、t-SNEという手法を使うことで、二次元や三次元の図として表現することができます。二次元とは平面、三次元とは立体のことです。このように次元を下げることで、データの全体像や、それぞれのデータの特徴が分かりやすくなります。
例えば、お店の顧客のデータがあるとします。顧客一人ひとりの年齢や購入履歴などの情報がたくさんあると、全体を把握するのは大変です。しかし、t-SNEを使って図にすると、似たような顧客が近くに集まって表示されます。これにより、顧客をいくつかのグループに分けたり、それぞれのグループがどのような特徴を持っているのかを、目で見てすぐに理解することができます。
また、画像データの場合も同様です。たくさんの画像データの中から、似た画像を見つけ出すのは容易ではありません。しかし、t-SNEを使うと、似た画像は図の中で近くに配置されるため、画像の分類や、通常とは異なる画像を見つけるのに役立ちます。例えば、工場で製造される製品の画像データを使って、不良品を自動的に検出するシステムを作ることも可能になります。
このように、t-SNEを使って図にすることで、データの全体像を把握し、隠れた特徴を発見することができます。データ分析の最初の段階において、t-SNEは強力な道具となるでしょう。
パラメータ調整の重要性

図表を視覚的に分かりやすく示す手法の一つに、次元を縮小して表示する方法があります。この手法は、多次元の情報を二次元や三次元に変換することで、人間の目で見て理解しやすい形にするものです。この際に、変換の過程で情報の歪みを最小限に抑え、元のデータの特徴をなるべく正確に反映させることが重要となります。次元縮小の手法の一つであるt-SNE(ティー・スニー)では、「近傍数」と呼ばれる設定値が、変換の精度に大きく影響します。この近傍数は、変換の際にどの程度の範囲のデータ点を互いに関連づけて扱うかを決定するものです。
この近傍数を適切に設定することで、データの持つ本来の構造をより正確に反映した視覚化結果を得ることが可能となります。近傍数は「パープレキシティ」とも呼ばれ、この値の設定がt-SNEを用いたデータ可視化の成否を分ける鍵となります。もし、パープレキシティの値が小さすぎると、データの局所的な、つまり狭い範囲の関係性のみが強調されてしまい、全体像を把握することが難しくなります。例えば、日本地図を描く際に、近所の家の配置ばかりに注目して、都道府県の位置関係を無視してしまうようなものです。逆に、パープレキシティの値が大きすぎると、今度は大域的な、つまり広い範囲の関係性のみが強調され、細かな構造が見えなくなってしまいます。これは、日本地図を描く際に、日本全体の形状だけを捉えて、各都市の位置を無視してしまうようなものです。
最適なパープレキシティの値は、扱うデータの特性によって異なります。そのため、データに合わせて適切な値を見つけ出す必要があります。一般的には、5から50の範囲で、実際に試しながら最適な値を探し出すことが推奨されています。様々な値を試すことで、データの全体像と細かな構造の両方をバランスよく表現できる、最適な可視化結果を得ることができるでしょう。
| t-SNEのパラメータ | 値が小さすぎる場合 | 値が大きすぎる場合 | 最適な値 |
|---|---|---|---|
| 近傍数(パープレキシティ) | 局所的な関係性のみ強調 (例: 近所の家の配置のみ注目) |
大域的な関係性のみ強調 (例: 日本全体の形状のみ) |
データ特性による (一般的に5-50で試行) |
t-SNEの活用事例

t-SNE(ティー・スニー)は、高次元データを低次元空間、特に二次元平面に落とし込む手法です。この手法を使うことで、複雑なデータの構造を視覚的に把握し、隠れたパターンや関係性を発見することができます。さまざまな分野で、データ解析の強力な道具として活用されています。
生物学の分野では、遺伝子発現データの解析によく使われます。それぞれの細胞は、どの遺伝子がどれだけ活発に働いているかという情報で特徴付けられます。これは多くの遺伝子を扱うため、非常に高次元なデータとなります。t-SNEを用いることで、この高次元データを二次元平面に投影し、似た遺伝子発現パターンを持つ細胞を近くに配置することができます。これにより、細胞の種類や状態の違いを視覚的に把握することが可能となり、例えば、健康な細胞とがん細胞の集団を区別したり、発生過程における細胞の変化を追跡したりすることができます。
自然言語処理の分野でも、t-SNEは重要な役割を果たしています。単語の意味をベクトルで表現する「単語分散表現」は、数百次元といった高次元空間で表現されることが一般的です。「王様」や「女王様」といった意味の近い単語は、この高次元空間で近くに位置していると考えられます。t-SNEを用いることで、これらの単語分散表現を二次元平面に落とし込み、視覚化することができます。これにより、単語間の意味的な近さや関係性を視覚的に捉えることができ、言葉の意味構造の理解に役立ちます。
画像認識の分野では、画像の特徴量を可視化するためにt-SNEが利用されます。画像は、色や形、模様といった様々な特徴を持つ複雑なデータです。これらの特徴を数値化し、ベクトルとして表現したものが特徴量です。t-SNEを用いることで、高次元の特徴量空間を二次元平面に投影し、似た特徴を持つ画像を近くに配置することができます。これにより、画像の分類や異常検知に役立ちます。例えば、正常な製品の画像と不良品の画像をt-SNEで可視化することで、不良品の特徴を捉え、検出精度を高めることが期待できます。このように、t-SNEは高次元データを扱う様々な分野において、データの理解を深めるための強力なツールとなっています。
| 分野 | t-SNEの活用例 |
|---|---|
| 生物学 | 遺伝子発現データの解析。細胞の種類や状態の違いを視覚化し、健康な細胞とがん細胞の区別、発生過程における細胞の変化の追跡などを可能にする。 |
| 自然言語処理 | 単語分散表現の視覚化。単語間の意味的な近さや関係性を視覚的に捉え、言葉の意味構造の理解に役立つ。 |
| 画像認識 | 画像の特徴量の可視化。似た特徴を持つ画像を近くに配置することで、画像の分類や異常検知に役立つ。 |
