深層強化学習における連続値制御

AIを知りたい
先生、「連続値制御」って難しくてよくわからないんですけど、簡単に説明してもらえますか?

AIエンジニア
いいかい? 例えば、ロボットに何かを掴ませたいとしよう。ただ掴むだけでなく、どのくらいの強さで掴むかも大事だよね。この「強さ」のように、色々な値をとれるのが連続値なんだ。連続値制御は、AIがこのような連続値をうまく調整できるように学習させることだよ。

AIを知りたい
なるほど。掴む強さ以外にも、他にどんな例がありますか?

AIエンジニア
自動運転で車のハンドルをどのくらい切るのか、ロボットの腕をどの角度に動かすのかなども連続値だね。 こういった微妙な調整が必要な場面で、連続値制御は活躍するんだよ。
連続値制御とは。
人工知能の分野でよく使われる『連続値制御』について説明します。特に、深層強化学習という技術で、どのように『行動』を学習させるかという話に深く関わってきます。『左へ行く』『右へ行く』といった行動は、とびとびの値(離散値)として出力されます。しかし、スピードやロボットの進む角度などは、滑らかに変化する値(連続値)として出力する必要があります。このような、連続値で出力を調整する必要がある問題設定のことを『連続値制御問題』と言います。
連続値制御とは

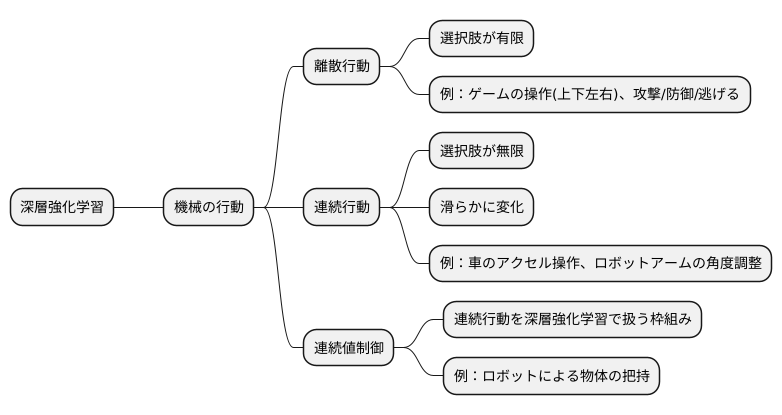
深層強化学習という技術は、機械に試行錯誤を通して物事を学習させる方法の一つです。まるで人間が経験から学ぶように、機械も様々な行動を試してみて、その結果から何が良かったのか、どうすればもっと良くなるのかを自分で考えていくのです。この学習の過程で、機械が取る行動には大きく分けて二つの種類があります。
一つ目は「離散行動」と呼ばれるものです。これは、選択肢がいくつか決まっていて、その中から一つを選ぶという行動です。例えば、テレビゲームでキャラクターを動かす時、「上」「下」「左」「右」のコマンドから一つを選びますよね。あるいは、「攻撃する」「防御する」「逃げる」といった選択肢から行動を決める場合もこれに当たります。このように、行動の選択肢が飛び飛びになっているのが離散行動の特徴です。
二つ目は「連続行動」です。こちらは選択肢が無限にあり、滑らかに変化する行動を指します。例えば、車の運転を想像してみてください。アクセルペダルをどのくらい踏むかによって、車の速度は微妙に変化します。少しだけ踏めばゆっくりと加速し、深く踏めば急発進します。ロボットアームの角度を調整する場合も同様です。微妙な角度の違いでロボットの動きは大きく変わります。このように、連続的な値で行動を調整するのが連続行動です。
そして、この連続行動を深層強化学習で扱う枠組みが「連続値制御」です。機械は、連続的な値を取りうる行動の中から、目的を達成するために最適な行動を学習しなければなりません。例えば、ロボットに物を掴ませる訓練をする場合、ロボットアームをどの角度、どの速度で動かせば掴めるのかを、連続値制御によって学習させるのです。
離散値制御との違い

物の動かし方を細かく指示するやり方と、そうでないやり方の違いについて説明します。
細かく指示するやり方、つまり離散値制御では、選べる行動の種類が決まっていて数が少ないです。例えば、ロボットに「前へ進む」「後ろへ下がる」「右へ曲がる」「左へ曲がる」の4つの行動だけを指示できるとします。この場合、それぞれの行動が良いか悪いかを簡単に調べることができます。それぞれの行動を試してみて、どの行動が一番良い結果になるかを記録すれば良いからです。数が少ないので、全部試すのも難しくありません。このように、一つ一つの行動の価値を調べて、一番価値の高い行動を選ぶというやり方が、離散値制御ではうまくいきます。
一方で、細かく指示しないやり方、つまり連続値制御では、選べる行動の種類が数え切れないほどたくさんあります。例えば、ロボットアームの角度を自由に設定できるとします。角度はほんの少しだけ変えることもできるので、可能な角度の組み合わせは無限に存在します。この場合、全ての行動を試すことは不可能です。全部試そうとすると、永遠に時間がかかってしまいます。そこで、連続値制御では別の方法を使います。
一つ目の方法は、行動を確率で表すというものです。ロボットアームの例で言うと、特定の角度にするのではなく、「この角度付近にする確率が高い」というように確率で表現します。そして、その確率に基づいてランダムに角度を選びます。こうすることで、色々な角度を試すことができます。
二つ目の方法は、行動を直接計算する式を作るというものです。この式を使えば、状況に応じて適切な角度を計算することができます。例えば、「目標物が右側にある場合は右に○度動かす」というような式を学習します。
このように、連続値制御では、離散値制御とは異なる、より複雑な計算方法が必要になります。しかし、そのおかげで、滑らかで正確な動きを実現することができます。
| 項目 | 離散値制御 | 連続値制御 |
|---|---|---|
| 行動の種類 | 有限個(例:前後左右) | 無限個(例:ロボットアームの角度) |
| 行動の決定方法 | 各行動の価値を評価し、最良の行動を選択 | 確率を用いる、または行動を計算する式を用いる |
| 評価方法 | 全行動を試すことが可能 | 全行動を試すことは不可能 |
| 例 | ロボットの移動方向 | ロボットアームの角度制御 |
| 特徴 | シンプル、理解しやすい | 複雑、滑らかで正確な動き |
連続値制御の応用例

連続値制御は、私たちの身の回りの様々な場面で活躍しています。滑らかに変化する量を扱う制御技術であるため、複雑な動きや繊細な調整が必要な場面で特に力を発揮します。
例えば、工場などで働くロボットアームを考えてみましょう。ロボットアームは、決められた位置に正確に部品を配置したり、溶接などの作業を行ったりします。これらの作業をスムーズかつ正確に行うためには、各関節の角度を連続的に制御する必要があります。連続値制御によって、ロボットアームは急激な動きをすることなく、目的の位置に正確に移動することができます。
自動運転技術においても、連続値制御は重要な役割を担っています。車の速度調整やハンドル操作は、連続的な入力によって行われます。アクセルペダルやブレーキペダルをどれくらい踏み込むか、ハンドルをどれくらい切るのかといった微妙な調整を連続値制御によって行うことで、車はスムーズに走行し、安全性を確保することができます。例えば、カーブを曲がるとき、ハンドルを一定の角度で固定するのではなく、カーブの曲率に合わせて滑らかに角度を変化させることで、快適な乗り心地を実現できます。
さらに、ゲームの世界でも連続値制御は欠かせません。ゲームキャラクターの自然で滑らかな動きは、連続値制御によって実現されています。例えば、格闘ゲームでキャラクターが繰り出す技の数々は、ボタンを押す長さやタイミングだけでなく、スティックの微妙な操作によって変化します。これらの複雑な操作を連続値制御によって処理することで、プレイヤーはキャラクターを思い通りに動かし、多彩な技を繰り出すことができます。また、レースゲームにおいても、アクセル、ブレーキ、ハンドルの微妙な操作が、マシンの挙動に大きな影響を与えます。連続値制御によって、プレイヤーは現実さながらの運転体験を楽しむことができます。
このように、連続値制御は、ロボット工学、自動運転、ゲームなど、様々な分野で利用されており、私たちの生活をより豊かに、より便利にするために欠かせない技術と言えるでしょう。
| 分野 | 例 | 連続値制御の役割 |
|---|---|---|
| ロボット工学 | ロボットアーム | 関節の角度を連続的に制御し、スムーズで正確な動作を実現 |
| 自動運転 | 車の速度調整、ハンドル操作 | 連続的な入力でスムーズな走行と安全性を確保 |
| ゲーム | キャラクターの動き、レースゲームの操作 | 滑らかで自然な動き、リアルな操作感を実現 |
課題と今後の展望

連続値制御という技術は、様々な可能性を秘めていますが、同時にいくつかの難題も抱えています。まず、「探索」と「活用」のバランスをうまくとることが重要です。連続的な行動の範囲の中では、最適な行動を見つけるために広い範囲を探し回る必要があります。しかし、既に見つけた良い行動をうまく活用して、学習を効率的に進めることも欠かせません。この両方のバランスをどのようにとるかが、大きな課題となっています。
次に、多くの要素が絡み合う複雑な状況での学習を、いかに効率化するかという問題があります。たとえば、多くの関節を持つロボットアームを制御する場合、動きの組み合わせは非常に多くなります。このような複雑な状況では、従来の方法では学習に時間がかかりすぎてしまいます。そのため、より効率的な学習方法を見つけることが急務となっています。
これらの課題を乗り越えることができれば、連続値制御の使い道は大きく広がると考えられます。たとえば、人とロボットが一緒に作業する場面や、家庭内でロボットが家事を手伝うといった、より複雑な作業を自動化できる可能性があります。さらに、深層学習といった新しい技術の進歩も、連続値制御の発展を後押ししています。今後、これらの技術がどのように発展していくか、注目していく必要があるでしょう。
| 課題 | 詳細 | 解決策の展望 |
|---|---|---|
| 探索と活用のバランス | 連続的な行動範囲で、最適な行動の探索と既知の良い行動の活用を両立させる必要がある。 | – |
| 複雑な状況での学習の効率化 | 多くの要素が絡み合う状況(例: ロボットアームの制御)での学習は、従来の方法では時間がかかりすぎる。 | より効率的な学習方法の開発が急務。 |
代表的なアルゴリズム

様々な場面で役立つ自動制御、特に滑らかに変化する値を扱う連続値制御においては、すぐれた計算手順が不可欠です。ここでは、代表的な計算手順をいくつか紹介します。
まず、決定論的方策勾配法を基にした計算手順である「深い決定論的方策勾配(DDPG)」があります。この手順は、方策と呼ばれる行動決定の指針を、状況に応じて確実に一つの行動を返す関数として学習します。つまり、同じ状況が与えられれば、常に同じ行動が返ってきます。この計算手順は、複雑な状況における制御問題で力を発揮します。
次に、「柔性俳優批評家(SAC)」と呼ばれる計算手順があります。これは、方策を確率的に表現する、つまり、同じ状況でも異なる行動をとる可能性があるように設計されています。また、この手順は「乱雑さ最大化」という工夫を取り入れており、様々な行動を試すことで、より良い行動を見つける可能性を高めています。SACは、DDPGと比べてより安定した学習が可能であり、様々な状況に柔軟に対応できるという利点があります。
DDPGとSAC以外にも、連続値制御に適した計算手順は存在します。例えば、「信頼領域方策最適化(TRPO)」や「近接方策最適化(PPO)」などです。TRPOは、方策の変化を制限することで安定した学習を実現する一方、PPOは計算コストを抑えつつTRPOと同等の性能を達成することを目指した計算手順です。
このように、連続値制御を実現するための計算手順には様々な種類があり、それぞれに得意な状況や不得意な状況が存在します。そのため、制御対象の特性を理解し、適切な計算手順を選択することが重要です。状況に応じて最適な計算手順を選ぶことで、より効果的な自動制御を実現できます。
| 計算手順名 | 説明 | 特徴 |
|---|---|---|
| 深い決定論的方策勾配 (DDPG) | 決定論的方策勾配法に基づき、状況に応じて確実に一つの行動を返す関数を学習する。 | 複雑な状況における制御問題で力を発揮する。 |
| 柔性俳優批評家 (SAC) | 方策を確率的に表現し、同じ状況でも異なる行動をとる可能性があるように設計。「乱雑さ最大化」を取り入れ、様々な行動を試すことで、より良い行動を見つける可能性を高める。 | DDPGと比べてより安定した学習が可能。様々な状況に柔軟に対応できる。 |
| 信頼領域方策最適化 (TRPO) | 方策の変化を制限することで安定した学習を実現する。 | 安定した学習が可能。 |
| 近接方策最適化 (PPO) | 計算コストを抑えつつTRPOと同等の性能を達成することを目指した計算手順。 | 計算コストが低い。TRPOと同等の性能。 |
