行動価値関数:最善手を見つける道しるべ

AIを知りたい
先生、「行動価値関数」って、難しくてよくわからないです。簡単に説明してもらえますか?

AIエンジニア
そうだね、難しいよね。「行動価値関数」は、ある状況である行動をとった時に、将来どれくらい良い結果が得られるかを数値で表したものだよ。ゲームで例えると、今の場所でどのボタンを押すと、最終的に高い得点を得られるかを教えてくれる関数のようなものだね。

AIを知りたい
つまり、今どんな行動をすれば、最終的に一番いい結果になるかを教えてくれるってことですか?

AIエンジニア
その通り!まさにそういうことだよ。迷路で例えるなら、それぞれの分かれ道で、どの道を選べばゴールまで一番早く着けるかを教えてくれる地図のようなものだね。AIは「行動価値関数」を使って、一番良い結果が得られる行動を選び続けることで、目的を達成していくんだ。
行動価値関数とは。
人工知能の分野でよく使われる「行動価値関数」について説明します。行動価値関数は、ある状況から次の状況に移るときに、とる行動それぞれに割り当てられた値のことです。強化学習という学習方法では、最終的に得られる報酬の合計を最大にすることが目標です。そのため、状況価値関数と行動価値関数が重要になります。人工知能のエージェントは、行動価値関数の合計が最大になるように行動することで、最も短い道筋を見つけることができます。
行動価値関数の役割

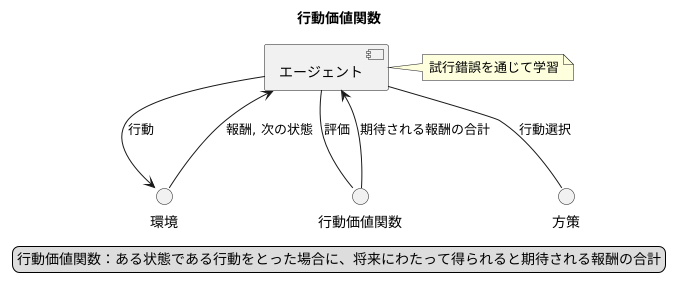
行動価値関数は、強化学習において行動の良し悪しを評価する重要な役割を担っています。強化学習とは、試行錯誤を通じて学習を行う仕組みであり、学習する主体であるエージェントが環境の中で最適な行動を習得することを目指します。最適な行動とは、長期的に見て最も多くの報酬を得られる行動のことです。
行動価値関数は、ある状態において特定の行動をとった場合に、将来にわたって得られると期待される報酬の合計値を表します。これは、目先の報酬だけでなく、将来得られる報酬も考慮に入れた評価基準となっています。例えば、将棋を考えると、目の前の駒を取る行動がすぐに大きな報酬をもたらすとは限りません。後々、より有利な展開に繋がる行動もあるからです。行動価値関数は、そのような将来の報酬まで見越した評価を可能にします。
エージェントは、この行動価値関数を基に行動を選択します。それぞれの行動に対応する行動価値関数の値を比較し、最も高い値を持つ行動を選ぶことで、長期的な報酬を最大化する戦略をとることができます。迷路を解くロボットを例に考えると、ロボットは各分岐点で、どの道に進むべきかを判断しなければなりません。各道に対応する行動価値関数の値が、その道を通ってゴールに到達するまでの期待される報酬を表しているとします。ロボットは、最も高い行動価値を持つ道を選ぶことで、ゴールへたどり着く可能性を高めることができます。
このように、行動価値関数は、エージェントが最適な行動を学習し、選択する上で、なくてはならない役割を果たしていると言えるでしょう。より多くの報酬を得られる行動を適切に評価することで、エージェントの学習を効率的に進めることができます。
状態と行動の繋がり

物事の状態と、それに対する行動には深い関わりがあります。 行動価値関数とは、ある状態における行動の価値を数値で表すものです。これは、現在の状況と行動の組み合わせによって決まります。たとえば、将棋を考えてみましょう。盤面の駒の配置、つまり現在の盤の状態が「状態」です。そして、どの駒をどこに動かすかという駒の動かし方が「行動」です。
行動価値関数は、特定の状態において、ある行動をとった場合に、将来的にどれだけの利益が得られるかを予測します。たとえば、ある局面で「飛車を二段目に動かす」という行動をとった場合、その後の展開でどれくらい有利になるかを予測するのです。この予測は、過去の対局データや、コンピュータが自ら学習した結果に基づいて行われます。将棋のプログラムは、様々な盤面と指し手の組み合わせを膨大に学習し、どの手がどれくらい有利かを計算します。
行動価値関数の値が高いほど、その行動は良い行動であると判断されます。将棋プログラムは、様々な行動の価値を計算し、最も価値の高い行動、つまり最も有利な手を選びます。このように、行動価値関数は、状態と行動の繋がりを数値化することで、どの行動が最適かを判断するのに役立ちます。
状態と行動の繋がりを理解することは、行動価値関数の本質を理解する上で非常に重要です。状態が変われば、最適な行動も変わります。盤面の状態によって、飛車を動かすのが良い手なのか、角を動かすのが良い手なのかが変わってくるのと同じです。状態と行動の繋がりを深く理解することで、人工知能がどのように学習し、判断を下しているのかをより良く理解することができます。
| 概念 | 説明 | 例(将棋) |
|---|---|---|
| 状態 | 物事の現在の状況 | 盤面の駒の配置 |
| 行動 | 状態に対する働きかけ | 駒の動かし方 |
| 行動価値関数 | ある状態における行動の価値を数値で表す関数。将来得られる利益を予測する。 | 特定の盤面で「飛車を二段目に動かす」という行動の価値(将来どれくらい有利になるか) |
累計報酬の重要性

行動の良し悪しを判断するには、目先の報酬だけでなく、その行動が将来もたらす報酬すべてを考え合わせる必要があります。これを測る尺度となるのが行動価値関数です。行動価値関数は、ある行動をとったときに、今すぐ得られる報酬だけでなく、その後に続くすべての報酬の合計を計算します。つまり、長期的な視点で行動の価値を評価するのです。
例えば、投資の世界を考えてみましょう。ある投資家は、短期的な利益に目がくらんで、リスクの高い投機に走ってしまうかもしれません。しかし、行動価値関数は、短期的な利益だけでなく、将来にわたって得られるであろう利益、そして損失の可能性も考慮します。賢明な投資家は、目先の利益にとらわれず、長期的な資産増加を見据えて行動します。これが、行動価値関数が示す考え方です。
将来の報酬を現在の価値に置き換えるために、割引係数というものが使われます。これは、将来の100円が現在の何円に相当するかを表す数値です。割引係数は、0から1の間の値をとります。割引係数が小さいほど、将来の報酬を軽視し、目先の報酬を重視するようになります。例えば、割引係数が0に近い場合、遠い将来に得られる報酬はほとんど無視されます。逆に、割引係数が1に近いほど、将来の報酬を重視し、長期的な利益を追求するようになります。
この割引係数は、状況に合わせて適切に設定する必要があります。例えば、すぐに結果が求められる状況では、割引係数を小さく設定することで、短期的な成果を重視することができます。一方、長期的な視点が重要な状況では、割引係数を大きく設定することで、将来の大きな利益を目指せます。このように、割引係数を調整することで、短期的な利益と長期的な利益のバランスをとることができるのです。
| 概念 | 説明 | 例 |
|---|---|---|
| 行動価値関数 | ある行動をとったときに得られる、現在と将来のすべての報酬の合計を計算する関数。長期的な視点で行動の価値を評価する。 | 投資において、短期的な利益だけでなく、将来にわたる利益と損失の可能性を考慮する。 |
| 割引係数 | 将来の報酬を現在の価値に置き換えるための係数。0から1の間の値をとる。 | 割引係数が小さい(0に近い)ほど目先の報酬を重視し、大きい(1に近い)ほど将来の報酬を重視する。 |
学習による最適化

物事を行う際の価値を数値で表したものを、行動価値関数といいます。この関数は、固定されたものではなく、経験を通して学習し、より良いものへと変化していきます。
たとえば、迷路を解くロボットを想像してみてください。ロボットは、まず様々な行動を試します。この時点では、どの行動が良いのか、ロボット自身も分かっていません。つまり、行動価値関数の値は最初ははっきりしていません。
ロボットが迷路の中を動き回る中で、壁にぶつかったり、ゴールにたどり着いたりといった経験をします。これらの経験から、どの行動がどの程度の価値を持つかを学習していきます。たとえば、壁にぶつかる行動は価値が低く、ゴールに近づく行動は価値が高いと判断します。
ロボットは、経験を積むごとに行動価値関数を更新していきます。価値の高い行動はより多く選択されるようになり、価値の低い行動は避けられるようになります。このように、試行錯誤を繰り返すことで、迷路を解くための最適な行動を見つけ出すのです。
この学習方法には、様々な種類があります。よく知られているものとして、キュー学習やサーサ学習などがあります。これらの学習方法は、行動価値関数を効率よく学習するための手順を定めたものです。
学習の目標は、最適な行動戦略を見つけることです。最適な行動戦略とは、どのような状況でも、最も高い価値を生み出す行動を選択できるようになることです。ロボットの例でいえば、最短経路で迷路を脱出できるようになることです。このように、行動価値関数の学習は、様々な場面で最適な行動を選択するために役立ちます。
| 用語 | 説明 | 例 |
|---|---|---|
| 行動価値関数 | 物事を行う際の価値を数値で表したもの。経験を通して学習し、より良いものへと変化する。 | 迷路を解くロボットの場合、各地点でどの方向に進むのが良いかを数値で表す。 |
| 学習プロセス | 最初は行動価値関数の値ははっきりしない。経験(例:壁にぶつかる、ゴールに到達する)を通して、どの行動がどの程度の価値を持つかを学習し、行動価値関数を更新。価値の高い行動はより多く選択され、価値の低い行動は避けられるようになる。 | ロボットが迷路内を移動し、壁にぶつかったりゴールに到達したりする中で、各地点での移動方向の価値を更新していく。 |
| 学習方法の種類 | キュー学習、サーサ学習など。行動価値関数を効率よく学習するための手順を定めたもの。 | ロボットが迷路を学習する際に、キュー学習やサーサ学習を用いる。 |
| 学習の目標 | 最適な行動戦略を見つけること。どのような状況でも、最も高い価値を生み出す行動を選択できるようになること。 | ロボットが最短経路で迷路を脱出できるようになる。 |
最短経路の探索

目的地まで最速でたどり着く方法は誰もが知りたい情報です。この探し方を最短経路探索といい、カーナビや地図アプリなどで日々使われています。最近では、ゲームのキャラクターの動きにも使われていて、私たちの生活に欠かせない技術となっています。
この技術を実現するのに重要な役割を果たしているのが、行動価値関数です。行動価値関数は、ある地点から目的地までの移動にかかる時間や費用などを数値化したものと考えてください。例えば、道路の混雑状況や信号の待ち時間、電車の乗り換え時間などを数値で表します。カーナビで考えると、ある交差点に差し掛かった時、右に曲がると目的地までの時間が10分、左に曲がると5分、直進すると7分かかるといった情報が行動価値関数に反映されます。
最短経路探索では、この行動価値関数を用いて、目的地までのコストが最小になる経路を探します。例えば、先ほどの交差点の例では、左に曲がるのが最も早く目的地にたどり着けるので、カーナビは左折を指示します。このように、各地点で行動価値関数を比較し、最も小さな値を持つ行動を選択していくことで、最終的に目的地までの最短経路を見つけ出すことができます。
行動価値関数は、状況の変化に合わせて柔軟に対応できるという利点もあります。例えば、道路の事故情報が入ってきた場合、カーナビは行動価値関数を更新し、事故を避けたルートを再計算します。これにより、常に最新の状況を反映した最適な経路案内が可能となります。このように、行動価値関数を用いた最短経路探索は、様々な分野で活用され、私たちの生活をより便利にしています。
| 用語 | 説明 |
|---|---|
| 最短経路探索 | 目的地まで最速でたどり着く方法を探すこと。カーナビや地図アプリ、ゲームのキャラクターの動きなどに使われている。 |
| 行動価値関数 | ある地点から目的地までの移動にかかる時間や費用などを数値化したもの。道路の混雑状況、信号の待ち時間、電車の乗り換え時間などが反映される。 |
| 行動価値関数の活用例 | 交差点で、右折10分、左折5分、直進7分かかる場合、左折が最短経路と判断される。 |
| 行動価値関数の利点 | 状況の変化に柔軟に対応できる。道路の事故情報などに応じて、ルートを再計算できる。 |
行動価値関数の限界

行動価値関数は、ある状態である行動をとったときの将来の累積報酬の期待値を表すもので、強化学習において重要な役割を担っています。まさに、エージェントがどの行動を選択すべきかを判断するための指針となるからです。しかし、万能のように見えるこの行動価値関数にも、いくつかの限界が存在します。
まず、状態空間や行動空間が膨大な場合、行動価値関数を正確に計算することが困難になります。例えば、囲碁のようなゲームを考えてみましょう。盤面の状態や可能な手の数は天文学的数字になり、すべての状態と行動の組み合わせについて価値を計算するのは現実的ではありません。このような場合は、関数近似や階層型強化学習といった手法を用いて、計算量を削減する工夫が必要となります。関数近似では、複雑な関数をより単純な関数で近似することで計算を簡略化します。階層型強化学習では、複雑なタスクを複数の階層に分解し、それぞれの階層で学習を行うことで、全体としての学習効率を高めます。
次に、環境が動的に変化する場合、せっかく学習した行動価値関数が最適ではなくなる可能性があります。例えば、ロボットが動作する環境に突如障害物が現れたとします。学習済みの行動価値関数は障害物のない環境を前提としているため、そのままでは適切な行動を選択できません。このような状況に対応するためには、オンライン学習や適応学習といった手法が有効です。オンライン学習では、刻々と変化する環境の情報を取り込みながら、行動価値関数を逐次更新します。適応学習では、過去の経験を活かしつつ、変化した環境に適応するように学習を行います。
最後に、行動価値関数は報酬関数に基づいて学習されます。報酬関数は、エージェントがどのような行動をすれば良いかを指示する役割を担いますが、この報酬関数の設計が不適切だと、エージェントは意図しない行動を学習してしまう可能性があります。例えば、掃除ロボットにゴミを吸い取る量だけを報酬として与えると、ロボットはゴミをまき散らしてから吸い取るという行動を学習するかもしれません。これは、ゴミを吸い取る量が増えるため、報酬が高くなるとロボットが判断するからです。このように、報酬関数の設計は慎重に行わなければなりません。適切な報酬関数を設計するためには、目的とする行動を明確に定義し、その行動に繋がる報酬を与える必要があります。
これらの限界を理解し、適切な対策を講じることで、行動価値関数をより効果的に活用し、強化学習による成果を最大化することができます。
| 限界 | 説明 | 対策 |
|---|---|---|
| 状態空間・行動空間の膨大さ | 状態や行動が多すぎると、全ての行動価値を計算するのが困難。 | 関数近似、階層型強化学習 |
| 環境の動的変化 | 学習済みの行動価値関数が、変化した環境では最適ではなくなる。 | オンライン学習、適応学習 |
| 報酬関数の設計の難しさ | 不適切な報酬関数だと、意図しない行動を学習する可能性がある。 | 目的とする行動を明確に定義し、それに繋がる報酬を与える。 |
