学習の加速:モーメンタム

AIを知りたい
先生、「モーメンタム」っていうAIの用語がよくわからないのですが、教えていただけますか?

AIエンジニア
いいですよ。「モーメンタム」は、AIの学習を速くするための方法です。 例えば、山登りを想像してみてください。平らな場所に来ると、どっちに登ればいいのかわからなくなってしまいますよね?モーメンタムは、そういう場所で、前に進んでいた勢いを利用して、そのまま進んでみるような仕組みです。

AIを知りたい
なるほど。平らな場所って、勾配が0の点のことですか?

AIエンジニア
そうですね。勾配が0に近い、ほとんど平らな場所のことを『鞍点』と呼びます。 そこでは、どちらに進んでいいのかわからず、学習が止まってしまうことがあります。モーメンタムは、これまでの学習の勢いを利用することで、この鞍点を乗り越えやすくするのです。
モーメンタムとは。
人工知能の分野でよく使われる『勢い』という用語について説明します。『勢い』とは、1990年代に考え出された方法で、学習の進み具合が止まってしまう『鞍点』と呼ばれる地点から抜け出すための技術です。学習を進める良い方向へ、より速く学習を進めることで、この停滞を打破します。鞍点の周辺では、学習の向きを示す『勾配』はゼロではありません。そのため、学習を加速することで、鞍点から抜け出すことができるのです。
はじめに

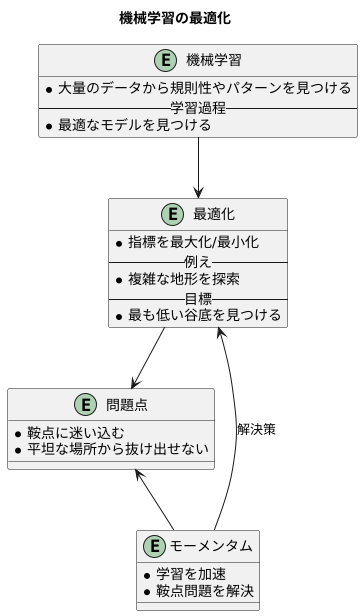
機械学習は、大量のデータから規則性やパターンを見つけることを目的とした技術です。この学習過程では、最適なモデルを見つけることが非常に重要になります。モデルの良し悪しを評価する指標があり、この指標を最大化あるいは最小化するモデルを見つける作業を最適化と呼びます。この最適化は、複雑な地形を探索する作業に例えられます。
最適化の目標は、指標を表す地形の最も低い谷底を見つけることです。低い場所ほど良いモデルを表しており、最も低い谷底が最も良いモデルに対応します。しかし、この地形は単純なものではなく、山や谷が複雑に入り組んでいます。そのため、単純な探索方法では、なかなか最適な谷底にたどり着けません。特に、鞍点と呼ばれる平坦な場所に迷い込んでしまうことがしばしばあります。鞍点は、ある方向から見ると谷底のように見えますが、別の方向から見ると頂上です。このため、通常の探索方法では、鞍点から抜け出すのが難しく、最適なモデルにたどり着けないという問題が発生します。
この問題を解決するために、1990年代にモーメンタムと呼ばれる手法が開発されました。この手法は、最適化の進行方向に学習を加速させるという画期的な考え方を取り入れています。ボールが斜面を転がり落ちるように、最適化の勢いを利用することで、鞍点のような平坦な場所でも勢いよく通り抜けることができます。このモーメンタムという手法は、機械学習の最適化において、鞍点問題を解決するための重要な技術となっています。これにより、より良いモデルの探索が可能になり、機械学習技術の発展に大きく貢献しています。
勾配降下法の課題

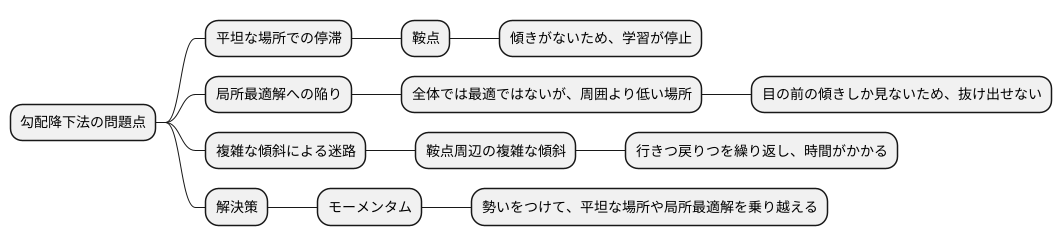
坂を下ることで最も低い場所を探す方法、勾配降下法には、いくつかの問題点が潜んでいます。この方法は、現在の場所の傾きだけを手がかりに進むため、平坦な場所に差し掛かると、まるで迷子のように彷徨ってしまいます。傾きがほとんど無い平坦な場所は、鞍点と呼ばれ、勾配降下法にとって大きな障壁となります。ちょうど、ボールが平地で止まってしまうように、学習の進みが止まってしまうのです。
鞍点の問題は、単に学習が遅くなるだけではありません。鞍点の周辺は、傾斜が複雑に変化していることが多く、まるで迷路のように、何度も行きつ戻りつを繰り返すことになります。そのため、真に最も低い場所、つまり最適な解にたどり着くまでに、非常に長い時間がかかってしまうのです。目的地まで真っ直ぐ行けると思いきや、何度も遠回りをしてしまう、そんなイメージです。
さらに、局所最適解という落とし穴も存在します。これは、全体で見れば最も低い場所ではないものの、周囲と比べて低い場所のことです。勾配降下法は、目の前の傾きしか見ていないため、このような局所最適解に捕まってしまうと、そこから抜け出せなくなってしまいます。まるで深い穴に落ちてしまったように、そこから脱出するのは困難です。
このような勾配降下法の抱える問題点を解決するために、様々な改良が試みられています。例えば、「勢い」をつけて進むことで、平坦な場所や局所最適解を乗り越えやすくする工夫などが提案されています。この勢いをつける方法は「モーメンタム」と呼ばれ、勾配降下法の弱点を克服する一つの手段として注目されています。
モーメンタムの仕組み

学びの道筋をうまく見つけるための方法の一つに、勢いを大切にする考え方があります。この考え方を『モーメンタム』と呼び、まるでボールが坂道を転がるように、過去の動きの情報を活かして、より早く、より確実に学びを進めることができます。
ボールが坂道を転がる様子を思い浮かべてみてください。坂道を下るにつれて、ボールはどんどん速さを増していきます。そして、平らな場所にたどり着いても、しばらくは進み続けますよね。これは、ボールがそれまでの動きの勢いを保っているからです。モーメンタムもこれと同じように、過去の学びで得られた傾きの情報を蓄積し、現在の傾きと組み合わせることで、学びの勢いを保ち続けるのです。
学びの道のりは、必ずしも平坦ではありません。山あり谷ありで、時には平坦な場所が現れることもあります。このような平坦な場所は、まるで馬の鞍のような形をしていることから『鞍点』と呼ばれ、学びが進みにくくなる難所として知られています。しかし、モーメンタムは、過去の勢いを活かすことで、この鞍点のような平らな場所でも勢いよく突き進むことを可能にし、難所を突破する助けとなります。
さらに、モーメンタムには、学びの道のりを安定させる効果もあります。学びの過程では、最適な道筋を探るために、右に行ったり左に行ったりと、まるで迷子のように彷徨ってしまうことがあります。このような迷いを『振動』と呼びますが、モーメンタムは過去の傾きの情報を考慮することで、この振動を抑え、より安定した学びを実現します。
このように、モーメンタムは、過去の学びを活かすことで、より速く、より安定した学びを可能にする、強力な方法なのです。
| 概念 | 説明 | 類 analogy |
|---|---|---|
| モーメンタム | 過去の動きの情報を活かして、より早く、より確実に学びを進める考え方。 | 坂道を転がるボール |
| 鞍点 | 学びの道のりで、平坦で進みにくい場所。 | 馬の鞍 |
| 振動 | 最適な道筋を探る過程で、右往左往してしまう迷い。 | 迷子 |
| モーメンタムの効果 | 鞍点の突破、振動の抑制、学習の加速と安定化 | – |
モーメンタムの利点

機械学習において、学習過程を速く安定させることは非常に重要です。そのために広く使われている手法の一つに、運動量を意味する「モーメンタム」があります。モーメンタムは、まるでボールが坂道を転がるように、過去の動きを現在の更新に反映させることで、学習の効率と安定性を高めます。
まず、モーメンタムは学習速度を向上させます。勾配降下法などの最適化アルゴリズムは、パラメータを少しずつ調整しながら、損失関数が最小となる値を探します。しかし、平坦な領域(鞍点)に遭遇すると、勾配がほぼゼロになるため、パラメータの更新が停滞し、学習が遅くなります。モーメンタムは、過去の動きの影響を保持することで、この鞍点から抜け出しやすく、より速く最適な解へと導きます。
次に、モーメンタムは学習の安定性を向上させます。勾配降下法では、谷間のように入り組んだ損失関数の地形において、パラメータの更新が振動し、学習が不安定になることがあります。モーメンタムは、過去の動きを平均化することで、この振動を抑制し、学習過程を滑らかにします。これにより、安定した学習が可能となり、より良いモデルが得られる可能性が高まります。
さらに、モーメンタムは局所最適解に陥るリスクを軽減します。局所最適解とは、一見すると最適な解のように見えますが、実際には全体で見ると最適ではない解のことです。例えるなら、複数の谷がある地形の中で、最も深い谷ではない谷底に迷い込んでしまうようなものです。モーメンタムは、過去の動きを利用することで、小さな谷底を飛び越え、より良い解、つまりより深い谷底へと到達する可能性を高めます。
このように、速度向上、安定性向上、局所最適解回避といった多くの利点を持つモーメンタムは、多くの機械学習アルゴリズムにおいて重要な役割を担っています。
| モーメンタムの利点 | 説明 |
|---|---|
| 学習速度の向上 | 過去の動きの影響を保持することで、損失関数の平坦な領域(鞍点)から抜け出しやすく、より速く最適な解へと導きます。 |
| 学習の安定性の向上 | 過去の動きを平均化することで、パラメータ更新の振動を抑制し、学習過程を滑らかにします。 |
| 局所最適解に陥るリスクの軽減 | 過去の動きを利用することで、小さな谷底を飛び越え、より良い解へと到達する可能性を高めます。 |
モーメンタムの適用例

機械学習の分野では、学習をより速く、より正確に進めるための様々な工夫が凝らされています。その中で、「モーメンタム」と呼ばれる手法は、近年注目を集めている重要な技術の一つです。この手法は、まるでボールが坂道を転がり落ちるように、学習の方向性を少しずつ調整することで、より良い結果へと導いてくれます。
具体的には、画像を見て何が写っているかを判断する画像認識や、人間が話す言葉を理解する自然言語処理、そして音声を認識する音声認識など、様々な場面でモーメンタムは活躍しています。特に、複雑な構造を持つ深層学習モデルや、膨大な量のデータを扱う際には、その効果が際立ちます。
モーメンタムを用いない場合、学習の過程は山登りに例えることができます。頂上(最適な状態)を目指して一歩ずつ登っていくのですが、谷に迷い込んでしまう可能性があります。モーメンタムは、この谷に落ち込むことを防ぎ、よりスムーズに頂上へと導く役割を果たします。過去の学習の履歴を考慮することで、現在の学習方向を調整し、より効率的に最適な状態へと近づけるのです。
例えるなら、自転車に乗ることを想像してみてください。ペダルを漕ぐのを急にやめても、自転車はすぐには止まりません。しばらくの間、慣性によって進み続けます。モーメンタムも同様に、過去の学習の「勢い」を保持することで、急な方向転換を避け、より安定した学習を実現します。
このように、モーメンタムは最新の学習方法の土台となる重要な技術であり、今後の機械学習の進歩においても、中心的な役割を担うことが期待されています。より速く、より正確な学習を実現するための、更なる発展が期待される、大変重要な技術なのです。
| 項目 | 説明 |
|---|---|
| 手法名 | モーメンタム |
| 概要 | 学習の方向性を少しずつ調整することで、より良い結果へと導く手法。過去の学習の履歴を考慮し、現在の学習方向を調整することで、より効率的に最適な状態へと近づく。 |
| 利点 | 学習をより速く、より正確に進める。谷に落ち込むことを防ぎ、スムーズに最適な状態へと導く。急な方向転換を避け、安定した学習を実現。 |
| 応用例 | 画像認識、自然言語処理、音声認識など |
| 効果的な場面 | 複雑な構造を持つ深層学習モデル、膨大な量のデータを扱う場合 |
| 例え | ボールが坂道を転がり落ちる様子、自転車の慣性 |
| 将来性 | 今後の機械学習の進歩において中心的な役割を担うことが期待されている。 |
まとめ

機械学習では、膨大なデータから規則性やパターンを見つけるために、最適な設定値を見つけ出す作業が欠かせません。この最適な設定値を見つける作業を最適化といい、そのために様々な工夫が凝らされています。その中で、モーメンタムは重要な手法の一つです。
モーメンタムは、勾配降下法と呼ばれる最適化手法を改良したもので、過去の勾配情報を活用することで、より効率的に最適な設定値に近づけることができます。勾配降下法は、現在の位置から見て最も急な下り坂の方向に進むことで、最適な設定値を探します。しかし、この方法には、谷がいくつもある複雑な地形では、局所的な谷に捕まってしまい、真の最適値に到達できないという問題点があります。
モーメンタムは、この問題を解決するために、過去の移動方向の情報を加味することで、慣性のような効果を生み出します。つまり、過去の移動方向の影響を受けて、局所的な谷を乗り越え、より良い設定値へと進みます。ボールが斜面を転がる様子を想像してみてください。ボールは、斜面の傾斜だけでなく、これまでの運動量も加味して動き続けます。モーメンタムも同様に、過去の勾配情報を運動量として利用することで、最適化の過程をスムーズに進めます。
これにより、学習速度が向上するだけでなく、鞍点と呼ばれる平坦な領域からの脱出も容易になります。鞍点では勾配がほぼゼロになるため、勾配降下法はそこで停止してしまいますが、モーメンタムは過去の運動量によって鞍点を乗り越えることができます。
モーメンタムは、様々な機械学習のアルゴリズムで広く使われており、画像認識や自然言語処理など、多くの分野で成果を上げています。近年、より高度な最適化手法が登場していますが、モーメンタムは今もなお重要な役割を果たし続けています。モーメンタムの基本的な仕組みを理解することは、機械学習の仕組みを深く理解する上で非常に重要です。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 勾配降下法 | 現在の位置から見て最も急な下り坂の方向に進むことで最適な設定値を探す。 | 実装が簡単。 | 局所的な谷に捕まりやすい。 鞍点で停止しやすい。 |
| モーメンタム | 勾配降下法に過去の移動方向の情報を加味した手法。慣性のような効果を生み出し、局所的な谷を乗り越えやすくなる。 | 学習速度が向上する。 鞍点からの脱出が容易になる。 |
– |
