ε-greedy方策:探索と活用のバランス

AIを知りたい
先生、『ε-greedy方策』って、どんなものですか?

AIエンジニア
そうだね。『ε-greedy方策』は、強化学習で使う方法の一つだ。簡単に言うと、いつも一番良さそうな行動を選ぶんじゃなくて、ときどき、わざと違う行動を試してみるんだよ。

AIを知りたい
わざと違う行動をするんですか? なぜですか?

AIエンジニア
いい質問だね。いつも一番良さそうに見える行動だけを選んでいると、もっと良い行動を見逃してしまうかもしれないだろ? だから、ときどき違う行動を試すことで、本当に一番良い行動を見つけられる可能性が高くなるんだ。ε-greedy方策では、εの値で、どれくらいの頻度で違う行動を試すかを決めるんだよ。
ε-greedy方策とは。
人工知能の分野でよく使われる『イープシロン-グリーディーほうさく』について説明します。これは、学習するコンピュータがより良い結果を得るための方法の一つです。コンピュータは、最終的には一番良い結果になるように行動することを目指しますが、いつも一番良さそうな行動だけをしていると、他の良い行動を見逃してしまう可能性があります。そこで、この『イープシロン-グリーディーほうさく』では、たまにわざとランダムな行動をとってみるのです。具体的には、『イープシロン』と呼ばれる確率で、でたらめに色々な行動を試します。そして、残りの確率(1からイープシロンを引いた確率)では、現在持っている情報の中で一番良さそうな行動を選びます。このように、ときどき冒険をすることで、より良い行動を見つけ出す可能性を高めているのです。
はじめに

強化学習とは、機械学習の一種であり、試行錯誤を通して学習する枠組みです。まるで迷路の中でゴールを目指すように、学習する主体である「エージェント」は、様々な行動を試しながら、どの行動が最も良い結果をもたらすかを学んでいきます。この学習の目的は、長期的視点に立った報酬を最大化することにあります。 一回の行動で得られる報酬だけでなく、将来にわたって得られる報酬の合計を最大にする行動を見つけ出すことが重要です。
しかし、最適な行動を見つけるのは簡単ではありません。すでに知っている情報に基づいて、最も良いと思われる行動を選ぶ「活用」だけでは、本当に最適な行動を見逃してしまう可能性があります。例えば、いつも同じ店でお昼ご飯を食べる「活用」ばかりしていると、もっと美味しいお店を見つける機会を失ってしまうかもしれません。そこで、未知の行動を試す「探索」が必要になります。新しいお店を探してみることで、今よりもっと美味しいお昼ご飯にありつけるかもしれません。
この「活用」と「探索」のバランスは、強化学習において非常に重要な課題であり、「活用」と「探索」のジレンマと呼ばれています。常に「活用」ばかりしていると、局所的な最適解に陥り、真に最適な行動を見つけることができません。逆に、常に「探索」ばかりしていると、せっかく良い行動を見つけても、それを十分に活用できず、報酬を最大化することができません。
ε-greedy方策は、この「活用」と「探索」のジレンマに対する、単純ながらも効果的な解決策の一つです。ε-greedy方策では、ある小さな確率εでランダムに行動を「探索」し、残りの確率(1-ε)で現在の知識に基づいて最も良いと思われる行動を「活用」します。このεの値を調整することで、「活用」と「探索」のバランスを制御することができます。εの値が大きいほど「探索」の割合が増え、小さいほど「活用」の割合が増えます。このように、ε-greedy方策は、限られた情報の中でも、効果的に最適な行動を学習するための手法と言えるでしょう。
方策の仕組み

方策とは、ある状況においてどのような行動をとるかを決めるための手順のことです。 方策の種類は様々ですが、その中でもε-greedy方策は、探索と活用のバランスを確率的に調整する方法として広く知られています。
ε-greedy方策では、まず小さな値εを設定します。このεは0から1の間の値で、探索の度合いを調整する役割を果たします。一般的には0.1などの小さな値が用いられます。
各場面において、計算機はεの確率で無作為な行動を選びます。これが探索にあたります。 無作為な行動は、これまで試したことのない行動を試す機会となり、より良い行動を見つける可能性を広げます。言わば、未知の領域を探検するようなものです。
一方、残りの1-εの確率では、これまでの経験から最も価値が高いと判断された行動を選びます。これが活用にあたります。 過去の経験から得られた知識を最大限に活かし、確実性の高い行動をとることで、より多くの報酬を得ることが期待できます。これは、過去の成功体験を基に最善と思われる行動をとるようなものです。
このように、ε-greedy方策は、εの値で探索と活用のバランスを調整することで、未知の行動の探索と既知の行動の活用を両立させ、最適な行動を見つけることを目指します。 εの値が大きいほど探索の割合が増え、小さいほど活用の割合が増えます。状況に応じてεの値を調整することで、より効率的に学習を進めることができます。
| 方策 | 説明 | 確率 |
|---|---|---|
| 探索(ランダムな行動) | これまで試したことのない行動を試す | ε |
| 活用(最善の行動) | これまでの経験から最も価値が高いと判断された行動をとる | 1-ε |
パラメータ調整

「パラメータ調整」は、機械学習において非常に重要な工程です。 パラメータとは、機械学習モデルの動作を制御する設定値のようなものです。この設定値を適切に調整することで、モデルの性能を最大限に引き出すことができます。
今回の記事では、特に「ε(イプシロン)」というパラメータについて詳しく説明します。εは、「探索」と「活用」のバランスを調整する役割を担います。
「探索」とは、未知の行動を試すことです。新しい可能性を探ることで、より良い結果に繋がるかもしれません。一方、「活用」とは、これまでの経験から最も良いと思われる行動を選ぶことです。確実な成果を得るためには、過去の成功事例を活かすことが重要です。
εの値が大きい場合、探索の割合が増加します。つまり、多くの新しい行動を試すことになります。これは、未知の領域に潜む最適な解を見つけるチャンスを広げます。しかし、既知の最適な行動を軽視してしまう可能性も秘めています。
逆に、εの値が小さい場合、活用の割合が増加します。つまり、過去の経験に基づいて最良と思われる行動を優先的に選択します。これにより、安定した成果を得やすくなります。ただし、局所的な最適解に囚われてしまい、真の最適解を見逃してしまう可能性も懸念されます。
最適なεの値は、扱う問題の種類や学習の進み具合によって変化します。一般的には、学習の初期段階ではεの値を大きく設定します。そして、学習が進むにつれて徐々にεの値を小さくしていきます。
学習の初期段階では、様々な行動を試すことで、最適な行動を見つける可能性を高めます。学習がある程度進んだ段階では、これまでの経験を活かして、最適な行動に焦点を絞っていくことが効率的です。このように、εの値を調整することで、探索と活用のバランスを最適化し、機械学習モデルの性能向上を図ることが可能になります。
| ε (イプシロン)の値 | 探索 | 活用 | 結果 |
|---|---|---|---|
| 大きい | 増加 (多くの新しい行動を試す) | 減少 | 未知の最適解発見の可能性向上、既知の最適行動軽視の可能性 |
| 小さい | 減少 | 増加 (過去の経験に基づいた行動選択) | 安定した成果、局所最適解に囚われる可能性 |
| 学習初期 | 大きい | 小さい | 様々な行動を試す |
| 学習後期 | 小さい | 大きい | 最適な行動に焦点を絞る |
利点と欠点

ε-greedy方策には、良い点と悪い点があります。まずは良い点から説明します。ε-greedy方策は、とても単純で実装しやすいことが大きな特徴です。複雑な計算は必要なく、少ない計算資源で動かすことができます。また、探索と活用のバランスを調整するパラメータはεだけで、この値を変えるだけで調整ができるため、とても簡単です。
次に悪い点について説明します。ε-greedy方策では、εの値があらかじめ決まっており、学習の進み具合に合わせて自動的に調整することができません。つまり、学習の初期段階では広い範囲を探索するためにεを大きく設定する必要がありますが、学習が進むにつれてεを小さく設定して活用の割合を増やす必要があります。しかし、ε-greedy方策ではεの値は固定されているため、このような動的な調整ができません。
また、ε-greedy方策では、εの確率でランダムな行動を選択します。これは、探索を行う上で重要な要素ですが、時には非効率な行動を選択してしまう可能性があります。例えば、既に最適な行動が見つかっているにも関わらず、ランダムな行動を選択してしまうことで、最適な行動を見逃してしまう可能性があります。
さらに、ε-greedy方策は局所的な最適解に陥る可能性があります。局所的な最適解とは、全体で見ると最適ではないものの、その周辺では最適な解のことです。ε-greedy方策では、εの確率でランダムな行動を選択するため、大域的な最適解に到達する前に、局所的な最適解に捕まってしまう可能性があります。つまり、より良い解が存在するにも関わらず、それを見つけられない可能性があるということです。これらの欠点を克服するために、εの値を動的に調整する手法や、より高度な探索アルゴリズムなどが提案されています。
| メリット | デメリット |
|---|---|
| 単純で実装が容易 | εの値が固定で、学習の進捗に合わせた動的な調整ができない |
| 計算資源が少なくて済む | εの確率でランダムな行動を選択するため、非効率な行動を選択する可能性がある |
| 探索と活用のバランス調整がεだけで容易 | 局所的な最適解に陥る可能性がある |
他の手法との比較

強化学習において、試行錯誤を通じて最適な行動を見つけるためには、「探索」と「活用」のバランスが重要です。すでに効果が高いと分かっている行動を「活用」する一方で、まだ試していない行動を「探索」することで、より良い行動を見つける可能性があります。ε-greedy方策は、このバランスを取るための簡単な手法の一つですが、他にも様々な手法が存在します。
ε-greedy方策は、一定の確率εでランダムな行動を「探索」し、残りの確率1-εで最も効果が高いと現在分かっている行動を「活用」します。この手法は単純で実装しやすいという利点がありますが、常に一定の確率でランダムな行動を取ってしまうため、非効率な探索となる可能性があります。
一方、Upper Confidence Bound (UCB) アルゴリズムは、それぞれの行動に「楽観的な評価値」を割り当て、その評価値が最も高い行動を選択します。この楽観的な評価値は、行動の平均報酬に加えて、その行動を試した回数が少ないほど大きくなる不確実性を考慮した項を含みます。つまり、UCBアルゴリズムは、試行回数の少ない、不確実性の高い行動を優先的に探索します。
Thompson Samplingは、それぞれの行動が持つ真の報酬の分布を推定し、その分布からサンプリングした値に基づいて行動を選択します。この手法は、不確実性をより直接的に考慮しており、UCBアルゴリズムと同様に、試行回数の少ない行動を効率的に探索することができます。
これらの手法は、ε-greedy方策よりも複雑な計算を必要としますが、多くの場合でより良い性能を発揮します。しかし、問題の性質や利用可能な計算資源によっては、ε-greedy方策の単純さが有利になる場合もあります。例えば、計算資源が限られている場合や、問題の構造が非常に複雑な場合には、ε-greedy方策のシンプルさが実装の容易さや計算速度の面でメリットとなります。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| ε-greedy | 一定確率εでランダム行動、1-εで最良行動 | 単純、実装しやすい | 非効率な探索の可能性 |
| UCB | 楽観的評価値が最も高い行動を選択(平均報酬+不確実性) | 試行回数の少ない行動を優先的に探索 | ε-greedyより複雑な計算 |
| Thompson Sampling | 真の報酬分布を推定し、サンプリング値で行動選択 | 不確実性を直接考慮、効率的な探索 | ε-greedyより複雑な計算 |
適用事例

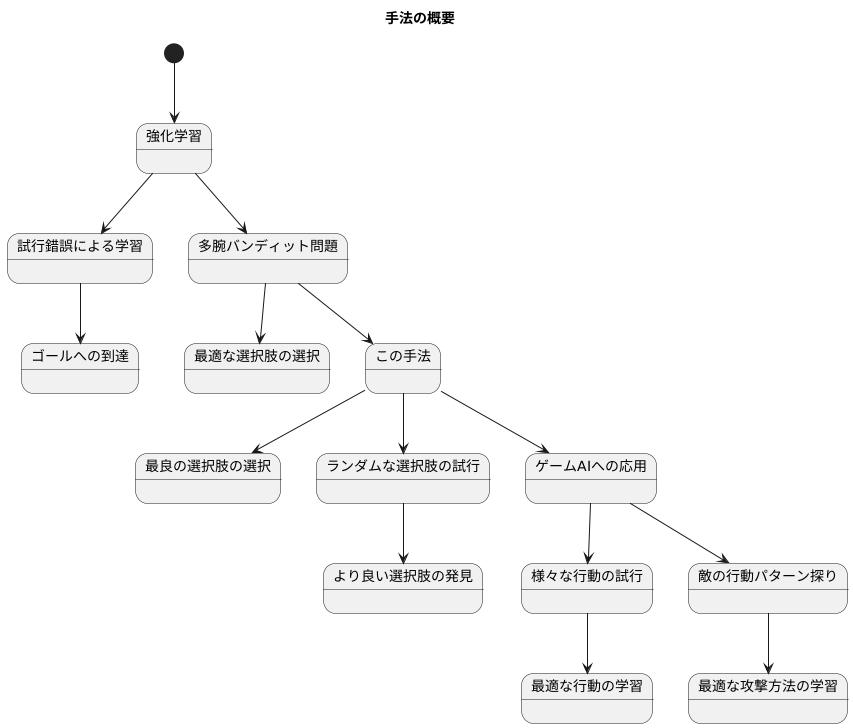
この手法は、様々な場面で使われています。特に、機械学習の中でも強化学習と呼ばれる分野でよく見られます。強化学習とは、試行錯誤を通じて学習していく方法です。まるで、迷路の中でゴールを目指すように、様々な行動を試してみて、どの行動が最も良い結果に繋がるのかを学んでいきます。
例えば、複数の選択肢から最適なものを選ぶ問題を考えてみましょう。これは、「多腕バンディット問題」と呼ばれています。複数のスロットマシンから、最もよく当たる台を選ぶ場面を想像してみてください。この問題を解くのに、この手法が役立ちます。
この手法は、常に最良だと思われる選択肢を選ぶだけでなく、ときどきランダムに別の選択肢を試します。このランダムな試行のおかげで、一見すると良くないように見える選択肢の中にも、実はより良い選択肢が隠れている可能性を探ることができます。いつも同じスロットマシンばかりを選んでいたら、他の台がもっと当たるかどうかは分かりませんよね?この手法は、まさにそのような探索を可能にします。
ゲームにおける人工知能の開発にも、この手法は応用されています。ゲームのキャラクターは、様々な行動を取ることができます。例えば、敵に攻撃したり、防御したり、逃げるなどです。どの行動が最適かは、敵の行動や状況によって変化します。この手法を使うことで、キャラクターは様々な行動を試しながら、どの行動が最も効果的かを学習できます。
敵の行動パターンを探りながら、最適な攻撃方法を学習する場面を想像してみてください。常に同じ攻撃ばかりしていると、敵にパターンを読まれてしまうかもしれません。しかし、ときどきランダムに違う攻撃を試すことで、敵の弱点を見つけたり、より効果的な攻撃方法を発見できるかもしれません。このように、この手法はゲームAIの学習に役立ちます。