ε-greedy方策:探索と活用のバランス

AIを知りたい
先生、「ε-greedy方策」って、結局どういうことですか? 最適な行動をとればいいのに、どうしてわざわざランダムな行動をとるんですか?

AIエンジニア
いい質問だね。いつも一番良いと思う行動だけをとっていると、他の選択肢を試す機会がなくなって、もっと良い行動があるかもしれないのに見逃してしまう可能性があるんだ。ε-greedy方策では、たまにランダムな行動をとることで、新しい行動を試して、より良い行動を見つけようとしているんだよ。

AIを知りたい
なるほど。でも、ランダムな行動をとるせいで、悪い結果になることもあるんじゃないですか?

AIエンジニア
その通り。確かに悪い結果になる可能性もある。でも、ランダムに行動する確率εは小さく設定されているから、多くの場合は最適な行動をとる。そして、たまにランダムな行動をとることで、長い目で見るとより良い行動を見つける可能性が高くなり、最終的にはより大きな報酬を得られる可能性があるんだ。
ε-greedy方策とは。
人工知能の学習方法の一つに、より良い結果を得るために試行錯誤を繰り返す「強化学習」というものがあります。その中で、「ε-グリーディー方策」という方法があります。これは、ほとんどの場合(1-εの確率で)は、現在持っている情報の中で一番良いと思われる行動を選びますが、ときどき(εの確率で)は、あえてランダムに行動を選びます。これは、いつも同じ行動ばかりしていると、他に良い行動があることに気づけない可能性があるからです。あえて違う行動を試すことで、より良い行動を見つけ出す可能性を広げているのです。
ε-greedy方策とは

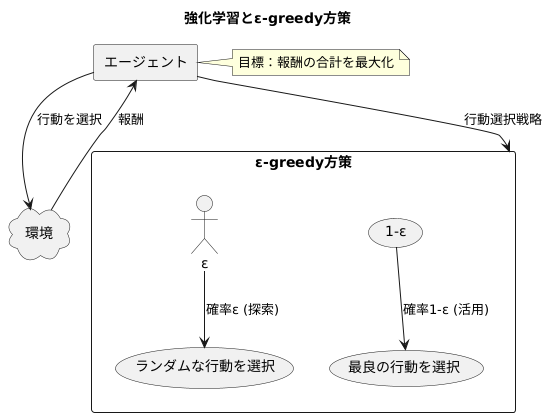
強化学習とは、機械学習の一種であり、試行錯誤を通して学習を行う仕組みです。まるで人間が新しい環境で生活を始めるように、初めは何も分からない状態から、様々な行動を試すことで、何が良くて何が悪いのかを徐々に学んでいきます。具体的には、学習を行う主体であるエージェントが、周りの環境と相互作用しながら行動を選択します。そして、その行動に対して環境から報酬が与えられます。ちょうど、良い行動をとれば褒められ、悪い行動をとれば叱られるようなものです。エージェントの最終的な目標は、行動によって得られる報酬の合計を最大にすることです。
このような強化学習において、ε-greedy方策は、エージェントが行動を選択するための効果的な戦略の一つです。ε-greedy方策の最大の特徴は、探索と活用のバランスをうまくとることです。探索とは、未知の行動を試すことで、より良い行動を見つける可能性を探ることです。活用とは、現時点で最も良いとわかっている行動を繰り返し行うことで、確実に報酬を得ることです。
ε-greedy方策では、あらかじめ小さな値ε(例えば0.1)を設定します。そして、エージェントは確率εでランダムな行動を選択します。これは探索に対応します。まるで、いつもと同じ道ではなく、たまには違う道を通ってみるようなものです。もしかしたら、近道が見つかるかもしれません。一方、残りの確率(1-ε)で、エージェントは現時点で最も良いとされている行動を選択します。これは活用に対応します。いつもと同じ道を通ることで、確実に目的地にたどり着くことができます。このように、ε-greedy方策は、探索と活用のバランスを調整することで、より多くの報酬を得るための行動選択を実現します。
探索の重要性

常に一番良いと思うことだけを選んで行動していると、もっと良い方法を見つける機会を逃してしまうことがあります。たとえば、食事をするお店でいつも決まったものばかり頼んでいると、実はもっと自分の好みに合う料理があることに気づかないかもしれません。
これは、機械学習における「探索」と「活用」という考え方にも当てはまります。「活用」とは、現在持っている知識に基づいて、最も良いと思われる行動を選ぶことです。一方、「探索」とは、現状より良い行動を見つけるため、あえて普段選ばない行動を試すことです。
ε-greedy方策という学習方法では、ある程度の確率でわざとランダムな行動を選びます。これは、いつも同じ行動ばかり取っていては、より良い行動にたどり着けない可能性があるからです。このランダムな行動が、まさに探索に相当します。
探索によって、これまで知らなかった、より良い行動を見つける可能性が広がります。特に学習の初期段階では、探索が非常に重要になります。なぜなら、学習を始めたばかりの段階では、機械はまだ周りの状況についてよく理解していません。そのため、色々な行動を試すことで多くの情報を集め、学習のスピードを速めることができるからです。
たとえば、新しいゲームを始めたばかりの時は、色々なボタンを押したり、キャラクターを色々な場所に移動させてみたりすることで、ゲームのルールや操作方法を早く覚えることができます。これと同じように、機械学習においても、初期段階での様々な試行錯誤が、後の学習効率を大きく左右するのです。
このように、常に最善と思われる行動だけを選ぶのではなく、時々は思い切った行動をとることで、最終的にはより良い結果に繋がる可能性があります。機械学習の世界では、このバランスが重要であり、適切な探索と活用のバランスによって、効率的な学習を実現できるのです。
| 概念 | 説明 | 機械学習における対応 | 例 |
|---|---|---|---|
| 活用 | 現在持っている知識に基づいて、最も良いと思われる行動を選ぶこと | ε-greedy方策において、確率の高い行動を選択 | いつも同じレストランで同じメニューを注文する |
| 探索 | 現状より良い行動を見つけるため、あえて普段選ばない行動を試すこと | ε-greedy方策において、確率の低い行動(ランダムな行動)を選択 | 新しいレストランで色々なメニューを試してみる 新しいゲームで色々なボタンや操作を試す |
| 探索の重要性 | 特に学習の初期段階では、より良い行動を見つけるために重要 多くの情報を集め、学習スピードを速める |
学習初期に様々な行動を試すことで、後の学習効率向上に繋がる | ゲーム初期に様々な操作を試すことで、ゲームのルールや操作方法を早く覚える |
| 探索と活用のバランス | 常に最善と思われる行動だけでなく、時々は思い切った行動をとることで、最終的に良い結果に繋がる | 適切なバランスによって、効率的な学習を実現 | – |
活用の重要性

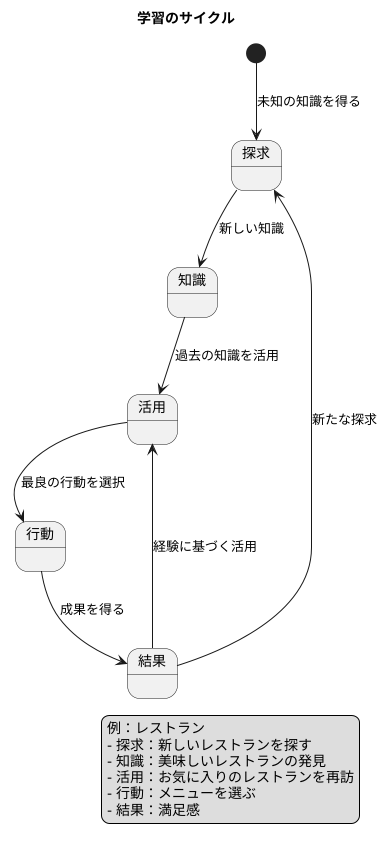
学習は、未知の世界を探求し新しい知識を得ることと、すでに得た知識を活用することの両輪で成り立っています。まるで、初めて訪れた町を散策するようなものです。まず、色々な場所を巡り、町の雰囲気やお店の場所などを把握します。この探索を通して、美味しいレストランを発見することもあるでしょう。しかし、常に新しいお店を探し続けるだけでは、既に見つけたお気に入りのレストランを再訪する機会を失ってしまいます。美味しいと分かっているお店に再び行くことは、過去の経験を活かして満足を得る行動です。これは、学習における「活用」の概念に繋がります。
例として、レストランで食事をする場面を考えてみましょう。様々な料理の中から、どれを選ぶか迷うこともあるでしょう。もし、毎回食べたいものを選ぶのではなく、ランダムにメニューを決めていたとしたらどうでしょうか?以前、とても気に入った料理があったとしても、再びそれを味わえるとは限りません。せっかく美味しいと知っているのに、それを選ぶ機会を逃してしまうのはもったいないことです。一方、過去の経験を基に「あの料理が美味しかった」と思い出し、同じメニューを選べば、再び満足を得られる可能性が高まります。これが活用の利点です。活用とは、過去の経験から得た知識を基に、最も良い結果が期待できる行動を選択することです。
学習が進むにつれて、この活用の重要性は増していきます。最初は、どの行動が良いか分からず、色々な選択肢を試す必要があります。しかし、経験を積むにつれて、どの行動がどの程度の成果に繋がるのか、徐々に分かってきます。環境についての知識が深まるほど、最良の行動を選択できるようになり、より大きな成果に繋がるのです。活用の重要性は、学習の成果を最大限に引き出すために不可欠です。過去の経験を活かし、より良い選択をすることで、学習の効果を最大化できるのです。
パラメータεの調整

ε-欲張り方策と呼ばれる手法は、うまく調整することで、行動の選択をうまく制御できます。この手法の鍵となるのがεと呼ばれる数値であり、この数値が方策の性能を大きく左右します。εは、探索と活用のバランスを調整する役割を担っています。
εの値を大きくすると、探索が活発になります。探索とは、未知の行動を試すことで、より良い行動を見つけ出す可能性を高めることです。まるで地図のない土地を探検するように、様々な行動を試すことで、思いがけない良い結果に繋がる可能性があります。学習の初期段階では、環境についてまだ十分な情報がないため、εを大きく設定して、積極的に探索を行うことが重要です。
一方、εの値を小さくすると、活用が重視されます。活用とは、過去の経験から最良と思われる行動を繰り返し選択することです。これまでの経験から得られた知識を最大限に活かすことで、効率的に報酬を得ることができます。学習が進むにつれて、環境についての理解が深まり、最適な行動が予測できるようになってきます。この段階では、εを小さく設定して、活用の割合を増やすことで、より多くの報酬を得ることが期待できます。
εの調整は、徐々に小さくしていくことが一般的です。学習の初期段階ではεを大きく設定して探索を重視し、学習が進むにつれてεを小さくして活用を重視するように調整します。これにより、最初は様々な行動を試しながら環境についての知識を蓄積し、徐々に最適な行動に収束していくことができます。まるで最初は広い範囲を探検し、徐々に有望な地域に絞り込んでいくようなイメージです。
ただし、εを小さくしすぎると、局所最適解に陥る可能性があります。局所最適解とは、全体で見れば最適ではないものの、その周辺では最適な解のことです。εが小さすぎると、探索が不足し、より良い解を見つける機会を失ってしまう可能性があります。常に一定の探索を続けることで、より良い解を発見する可能性を維持することができます。そのため、εの値は慎重に調整する必要があります。
| εの値 | 探索/活用 | 説明 | 適切な時期 |
|---|---|---|---|
| 大きい | 探索 | 未知の行動を試すことで、より良い行動を見つけ出す可能性を高める。 | 学習の初期段階 |
| 小さい | 活用 | 過去の経験から最良と思われる行動を選択し、効率的に報酬を得る。 | 学習が進んだ段階 |
εは徐々に小さくしていくことが一般的です。
εを小さくしすぎると、局所最適解に陥る可能性があります。
他の行動選択戦略との比較

強化学習における行動選択は、学習の効率と最終的な成果に大きく影響します。様々な行動選択戦略があり、それぞれに利点と欠点があります。ε-greedy方策は、最も基本的な戦略の一つであり、入門として広く使われています。この方法は、設定した確率εでランダムな行動を選び、残りの確率(1-ε)で最も価値が高いと推定される行動を選びます。このシンプルな仕組みのおかげで、実装が容易であり、多くの場面でまずまずの結果を得ることができます。しかし、常に一定の確率でランダムな行動をとるため、最適な行動を見つけた後でも、ときどき最適ではない行動を選んでしまう可能性があります。
一方、ソフトマックス方策は、各行動の価値を確率に変換して行動を選択します。価値が高い行動ほど選ばれる確率が高くなりますが、低い価値の行動にも選ばれるチャンスがあります。このため、ε-greedy方策よりも探索の幅が広がり、より良い行動を見つけられる可能性があります。ただし、計算コストがε-greedy方策よりも高くなる傾向があります。また、行動価値の差が小さい場合、選択の確率に大きな差がつきにくいため、最適な行動に収束しにくくなる場合があります。
UCB方策は、探索と活用のバランスをより洗練された方法で調整します。UCB方策は、各行動の価値に加えて、その行動がどれだけ試されたかを考慮に入れます。試行回数の少ない行動は不確実性が高いとみなし、価値にボーナスを加えて選択されやすくします。この仕組みにより、探索が不足している行動を積極的に試すことができます。結果として、ε-greedy方策よりも効率的に最適な行動を見つけられる可能性が高まります。ただし、UCB方策は実装が複雑になる場合があり、パラメータ調整も重要になります。
このように、それぞれの行動選択戦略には特徴があり、問題の性質や求められる性能に応じて適切な戦略を選択することが重要です。ε-greedy方策はシンプルで実装しやすい反面、最適な行動を見つける効率は他の戦略に劣る場合もあります。ソフトマックス方策は探索能力が高いですが、計算コストが高くなる可能性があります。UCB方策は探索と活用のバランスに優れていますが、実装の複雑さとパラメータ調整が課題となります。どの戦略を選ぶかは、状況に応じて慎重に検討する必要があります。
| 戦略 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| ε-greedy方策 | 確率εでランダムな行動を選択、確率(1-ε)で最も価値が高い行動を選択 | 実装が容易 多くの場面でまずまずの結果 |
最適な行動を見つけた後も、最適ではない行動を選んでしまう可能性がある |
| ソフトマックス方策 | 各行動の価値を確率に変換して行動を選択。価値が高い行動ほど選ばれる確率が高くなる | ε-greedy方策よりも探索の幅が広い より良い行動を見つけられる可能性がある |
計算コストが高い 行動価値の差が小さい場合、最適な行動に収束しにくい |
| UCB方策 | 各行動の価値と試行回数を考慮。試行回数の少ない行動にボーナスを加えて選択されやすくする | ε-greedy方策よりも効率的に最適な行動を見つけられる可能性が高い | 実装が複雑 パラメータ調整が重要 |
まとめ

まとめとして、ε-グリーディー方策は、強化学習における行動の選び方を決める基本的な方法です。この方法は、現状で最も良いとされている行動を選ぶ「活用」と、まだ試していない他の行動を試す「探索」のバランスを取ることが重要です。ε-グリーディー方策では、εという小さな値を使ってこのバランスを調整します。
具体的には、ランダムに選んだ0から1までの数値がεよりも小さい場合、探索を行います。つまり、現状で最適と考えられる行動とは関係なく、ランダムに他の行動を選択します。逆に、ランダムに選んだ数値がεよりも大きい場合は、活用を行います。つまり、現状で最も良いとされている行動を選びます。
εの値は、探索と活用の割合を調整する上で重要な役割を果たします。εの値が大きいほど探索の割合が増え、様々な行動を試すことができます。これにより、より良い行動が見つかる可能性が高まりますが、既知の最適行動を選ぶ機会が減るため、学習の速度が遅くなる可能性があります。一方、εの値が小さいほど活用の割合が増え、現状で最適とされる行動を頻繁に選択します。これにより、学習の速度は速くなりますが、局所的な最適解に陥り、真に最適な行動を見逃す可能性があります。
そのため、εの値は、問題の性質や学習の段階に応じて適切に調整する必要があります。例えば、学習の初期段階ではεの値を大きく設定して探索を重視し、学習が進むにつれてεの値を小さく設定して活用を重視するといった方法が有効です。
ε-グリーディー方策は、その簡潔さと効果から、強化学習の実用場面で広く使われています。さらに、より複雑な強化学習の手法を学ぶ上でも、ε-グリーディー方策は重要な基礎となります。探索と活用のバランスという考え方は、強化学習だけでなく、様々な場面での意思決定においても重要な視点となります。
| ε-グリーディー方策 | 説明 |
|---|---|
| 概要 | 強化学習における行動選択の基本的な方法。活用(現状で最良の行動)と探索(他の行動を試す)のバランスを調整。 |
| ε の役割 | 0 から 1 までの小さな値。探索と活用の割合を制御。 |
| 探索 | ランダムな数値が ε より小さい場合、ランダムに他の行動を選択。 |
| 活用 | ランダムな数値が ε より大きい場合、現状で最良の行動を選択。 |
| ε 値大 | 探索重視。学習速度は遅いが、より良い行動が見つかる可能性大。 |
| ε 値小 | 活用重視。学習速度は速いが、局所最適解に陥る可能性あり。 |
| ε 値調整 | 問題の性質や学習段階に応じて調整。初期は大きく、徐々に小さくするなどの方法。 |
| 利点 | 簡潔で効果的。強化学習の実用で広く使用。より複雑な手法の基礎。 |
