推移律：関係の連鎖を理解する

推移律：関係の連鎖を理解する

推移律：関係の連鎖を理解する

AIを知りたい

先生、「推移律」って難しくてよくわからないです。もう少し簡単に説明してもらえますか？

AIエンジニア

わかった。簡単に言うと、AさんとBさんが友達で、BさんとCさんも友達だったら、AさんとCさんも友達みたいな関係のことだよ。これを「AとBの関係」と「BとCの関係」から「AとCの関係」を導き出すルールと考えると、当てはまる場合もあるし、当てはまらない場合もあるんだ。

AIを知りたい

なるほど。友達の例えだとイメージしやすいです！でも、当てはまらない場合もあるんですか？

AIエンジニア

そうなんだ。例えば、「AさんはBさんの先生」で「BさんはCさんの先生」だとしても、「AさんはCさんの先生」とは限らないよね？推移律は、物事の関係を考える時の便利な道具だけど、いつでも使えるわけではないことを覚えておこうね。

推移律とは。

「人工知能でよく使われる言葉、『推移律』について説明します。推移律とは、ＡとＢに関係があり、ＢとＣにも関係があれば、ＡとＣにも自動的に関係ができるという法則です。例えば、『人』と『哺乳類』、『哺乳類』と『動物』という関係を考えたとき、『人』は『哺乳類』であり、『哺乳類』は『動物』であるなら、『人』は『動物』である、という関係が成り立ちます。これは『～は～である』という関係での推移律の例です。また、『東京』と『日本』、『日本』と『アジア』という関係を考えたとき、『東京』は『日本』の一部であり、『日本』は『アジア』の一部であるなら、『東京』は『アジア』の一部であるという関係も成り立ちます。これは『～は～の一部である』という関係での推移律の例です。ただし、関係の種類によっては推移律が成り立たない場合もあるので、注意が必要です。

推移律とは

推移律とは、物事の間にある種の関係があるとき、その関係が次々と繋がって成り立つ性質のことです。言い換えると、ＡとＢに特定の関係があり、同時にＢとＣにも同じ関係がある場合、ＡとＣにも必然的にその関係が成立する、という規則性を指します。

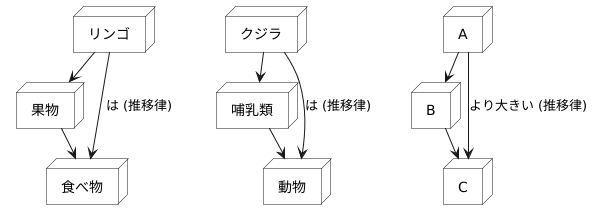
身近な例で考えてみましょう。例えば、「リンゴ」と「果物」の関係を考えてみます。リンゴは果物の一種なので、「リンゴ」は「果物」です。また、「果物」と「食べ物」の関係を見ると、果物は食べられるものなので、「果物」は「食べ物」です。これらの二つの関係から、推移律によって「リンゴ」は「食べ物」であるという新たな関係が導き出せます。これが推移律の働きです。

この性質は、様々な場面で応用できます。例えば、生き物の分類を理解する際に役立ちます。「クジラ」は「哺乳類」であり、「哺乳類」は「動物」です。これらの二つの関係から、推移律を用いると、「クジラ」は「動物」であるという結論が得られます。このように、既に分かっている二つの関係から、新たな関係を推論することができるのです。

また、大きさの比較でも推移律は成り立ちます。もし「Ａ」が「Ｂ」よりも大きく、「Ｂ」が「Ｃ」よりも大きいならば、必ず「Ａ」は「Ｃ」よりも大きいと言えるでしょう。これは、大小関係における推移律の典型的な例です。

このように、推移律は物事の関係性を理解し、新たな知識を導き出すための重要な考え方です。身の回りの様々な事柄に潜むこの性質を意識することで、より深く物事を理解できるようになるでしょう。

成立する例：is-a関係

「これはあれである」と言える関係を、専門的には「is-a関係」と呼びます。この関係は、あるものが別のものの種類に属することを示すものです。例えば、「犬は哺乳類である」というのが、is-a関係の一例です。犬は、哺乳類という大きなグループの中に含まれる一種である、という意味になります。

is-a関係には、「推移律」と呼ばれる重要な性質があります。推移律とは、AがBであり、BがCであるならば、AはCである、という論理的な規則のことです。is-a関係において、この推移律が成り立つということは、「犬は哺乳類である」そして「哺乳類は動物である」という二つのis-a関係から、「犬は動物である」という三つ目のis-a関係が必然的に導き出せることを意味します。

このis-a関係と推移律は、物事を整理して理解する上で大変役に立ちます。is-a関係を使うことで、色々な概念を階層構造として表現することができます。階層構造とは、上位概念と下位概念をピラミッドのように積み重ねた構造のことで、物事を分類したり、全体像を把握したりするのに役立ちます。

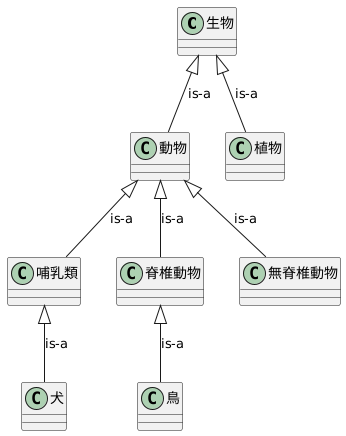
例えば、生物の分類を見てみましょう。生物全体を一番上に置き、その下に「動物界」や「植物界」といった大きなグループを置きます。さらに動物界の下には「脊椎動物門」や「無脊椎動物門」といったグループが続き、脊椎動物門の下には「哺乳綱」や「鳥綱」といったグループが続きます。このように、is-a関係を使って上位概念と下位概念を繋いでいくことで、複雑な生物界全体を整理された階層構造として表現することができます。生物学だけでなく、様々な分野でis-a関係と推移律は、物事を理解するための基本的な考え方として用いられています。

成立する例：part-of関係

あるものが別のものの一部であるという関係を『部分全体関係』と言います。この関係は、推移的な性質を持つため、考えを進める助けとなります。例えば、『東京都は関東地方の一部』であり、『関東地方は日本の一部』です。これらの二つの関係から、『東京都は日本の一部』という新しい関係が自然と導き出されます。これが、推移的な性質が成り立っている具体例です。

この『部分全体関係』は、様々な場面で活用できます。特に、物体の構成要素を表す際に有効です。例えば、複雑な機械を分解すると、多数の部品が現れます。それぞれの部品は機械の一部であり、さらに細かい部品で構成されている場合もあります。ネジや歯車は、エンジンの一部であり、エンジンは車全体の一部です。このように、『部分全体関係』を用いることで、複雑な機械の構造を分かりやすく整理できます。

また、地理的な関係を表す際にも、『部分全体関係』は役立ちます。例えば、東京都は関東地方の一部であり、関東地方は本州の一部、そして本州は日本列島の一部です。このように、大きな領域から小さな領域へと順を追って見ていくことで、それぞれの地域がどのような関係にあるのかを明確に理解できます。さらに、国と地方自治体の関係や、大陸と国、島と諸島といった様々な地理的関係も、『部分全体関係』で説明できます。

このように、『部分全体関係』は、物事の関係性を整理し、理解を深める上で重要な役割を果たします。複雑な事柄も、この関係を用いることで、単純で分かりやすい構造として捉えることができるのです。

成立しない例

物事の間のつながり方を示す法則である推移律は、どんなつながり方でも成り立つわけではありません。ある特定の条件が成り立つ場合、そこから導かれる結論が常に正しいとは限らないのです。

例えば、人のつながりを考えてみましょう。「AさんはBさんと友達である」と「BさんはCさんと友達である」という二つの関係があったとします。この時、推移律を適用すると「AさんはCさんと友達である」という結論が導き出されます。しかし、現実は必ずしもそうではありません。AさんとCさんが全く面識がない、つまり知り合いでないということもあり得るからです。Bさんを介して間接的につながってはいるものの、AさんとCさん自身が直接の友達関係にあるとは限りません。

他にも例を挙げましょう。「リンゴは果物である」と「果物は食べ物である」という二つの関係は正しいです。ここから推移律を適用すると、「リンゴは食べ物である」という結論になり、これは確かに正しいです。しかし、すべての関係において、このように推移律が成り立つとは限りません。

推移律が成り立つかどうかは、対象となる物事の関係の性質によって異なります。友達関係のように、直接的なつながりが必要な関係では、推移律は必ずしも成り立ちません。一方、リンゴと果物、果物と食べ物のような包含関係や、数学的な関係などでは、推移律が成り立つことが多いです。

推移律が適用できるかどうかを判断するには、関係の性質をしっかりと理解し、具体的な状況を丁寧に吟味することが重要です。そうでなければ、誤った結論に至ってしまう可能性があります。物事の間のつながり方を考える際には、常に注意深く、慎重に判断することが求められます。

前提1	前提2	結論（推移律適用）	結論の正しさ	関係の性質
AさんはBさんと友達	BさんはCさんと友達	AさんはCさんと友達	×	友達関係（直接的なつながり）
リンゴは果物	果物は食べ物	リンゴは食べ物	〇	包含関係

推移律の活用と注意点

ものの繋がりを考える上で、推移律はとても役に立つ考え方です。これは、ＡとＢに繋がりがあり、ＢとＣにも繋がりがある場合、ＡとＣにも繋がりがあると考えることです。例えば、りんごは果物であり、果物は食べ物であるならば、りんごは食べ物である、といった具合です。

推移律は、物事を整理したり、筋道を立てて考える際に力を発揮します。例えば、生物の分類を考える時、犬は哺乳類に属し、哺乳類は動物に属するならば、犬は動物に属すると考えることができます。このように、複雑な関係性を整理し、理解しやすくすることができます。

しかし、どんな繋がりにも推移律が当てはまるわけではありません。例えば、人間関係を考えてみましょう。ＡさんがＢさんの友達で、ＢさんがＣさんの友達だとしても、必ずしもＡさんとＣさんが友達であるとは限りません。これは、友達関係という繋がりが、必ずしも推移律に従わないからです。

また、親子関係でも同じことが言えます。ＡさんがＢさんの親で、ＢさんがＣさんの親だったとしても、ＡさんはＣさんの親ではありません。ＡさんはＣさんの祖父母にあたります。つまり、繋がり方の種類によって、推移律が成り立つかどうかが変わってくるのです。

推移律を使う際には、どのような繋がりについて考えているのかを注意深く見極める必要があります。物事の分類や包含関係などでは、多くの場合推移律が成り立ちますが、人間関係や位置関係などでは成り立たない場合も多いため、注意が必要です。状況に応じて、繋がり方の性質をしっかりと確認することで、誤った考え方を防ぎ、より正確に物事を理解することができるようになります。

繋がり	推移律の成立	例
りんご → 果物 → 食べ物	成立	りんごは果物であり、果物は食べ物であるならば、りんごは食べ物である。
犬 → 哺乳類 → 動物	成立	犬は哺乳類に属し、哺乳類は動物に属するならば、犬は動物に属する。
Aさん(友達)Bさん(友達)Cさん	不成立	AさんがBさんの友達で、BさんがCさんの友達だとしても、必ずしもAさんとCさんが友達であるとは限らない。
Aさん(親)Bさん(親)Cさん	不成立	AさんがBさんの親で、BさんがCさんの親だったとしても、AさんはCさんの親ではなく祖父母である。

まとめ

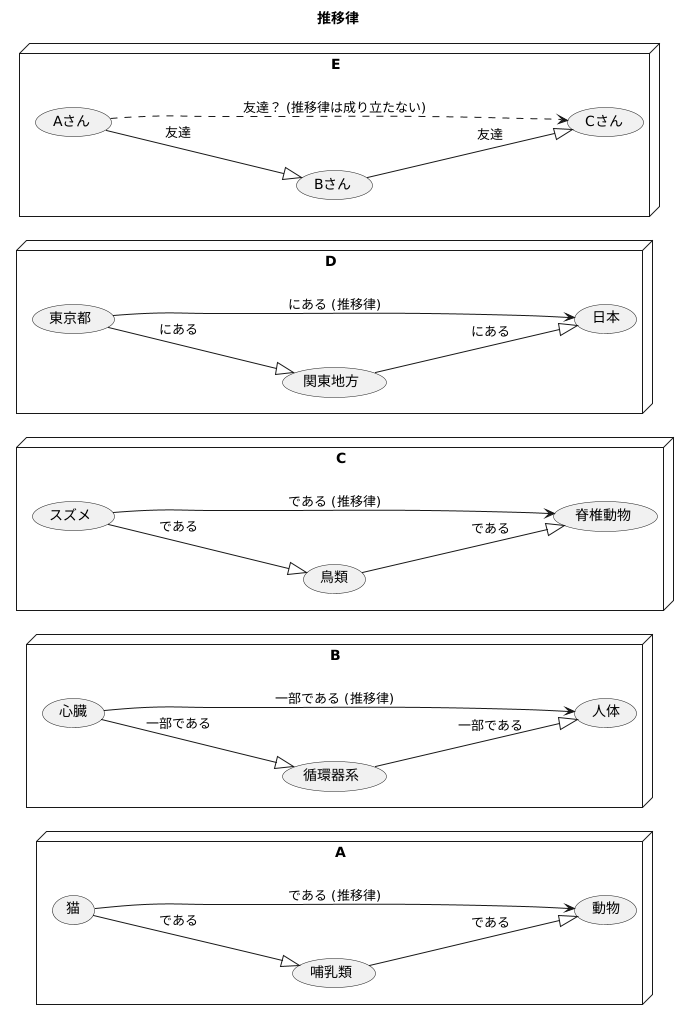
物事の間にある繋がりを考える上で、推移律という考え方を知っておくと便利です。推移律とは、ＡとＢ、そしてＢとＣに繋がりがあると分かっている時に、ＡとＣにも繋がりがあると推測できる性質のことです。この性質は、ある種の繋がりにおいてのみ成り立ちます。例えば、「ＡはＢである」という関係や「ＡはＢの一部である」という関係では、推移律が成り立ちます。具体的に考えてみましょう。もし「猫は哺乳類である」ことと、「哺乳類は動物である」ことが分かっていれば、推移律によって「猫は動物である」と推測できます。同様に、「心臓は循環器系の一部である」ことと「循環器系は人体の一部である」ことが分かっていれば、「心臓は人体の一部である」と推測できます。これらの例のように、推移律を使うことで、複雑な繋がりを整理し、新しい知識を導き出すことができます。

生物の分類や地理的な関係を理解する際にも、推移律は役立ちます。例えば、スズメは鳥類であり、鳥類は脊椎動物であることから、スズメは脊椎動物であると分かります。また、東京都は関東地方にあり、関東地方は日本にあることから、東京都は日本にあると分かります。このように、推移律は物事を階層的に理解するのに役立ち、知識の整理に役立ちます。しかし、全ての繋がりにおいて推移律が成り立つわけではありません。例えば、「ＡさんはＢさんと友達である」ことと「ＢさんはＣさんと友達である」ことが分かっていても、「ＡさんはＣさんと友達である」とは限りません。友達関係のように、推移律が成り立たない繋がりも存在します。ですから、推移律を当てはめる際には、その繋がりの種類をよく考えることが重要です。推移律を正しく理解し、適切に使うことで、筋道を立てて考え、問題を解決する能力を高めることができます。そのためには、様々な繋がりにおける推移律の条件や使える範囲を理解し、状況に応じて正しく判断する必要があります。