勾配消失問題:深層学習の壁

AIを知りたい
先生、「勾配消失問題」って、どういう意味ですか?難しそうです…

AIエンジニア
そうだね、少し難しいけど、図を使って説明するね。勾配消失問題は、高い建物の屋上から1階まで降りることを想像してみて。階段を一段ずつ降りるように、AIも学習データを使って少しずつ賢くなっていくんだ。この階段が「勾配」だよ。「勾配消失問題」は、階段を降りる途中で、階段が急に小さくなってしまい、ほとんど進めなくなってしまう状態なんだ。

AIを知りたい
なるほど。階段が小さくなる…ということは、AIが賢くなるのが遅くなるってことですか?

AIエンジニア
その通り!賢くなるのが遅くなるどころか、ほとんど賢くならなくなってしまうんだ。例えば、階段の段差を決める関数をシグモイド関数と呼ぶんだけど、この関数が階段をすごく小さくしてしまう原因の一つなんだよ。
勾配消失問題とは。
人工知能の分野でよく使われる言葉に「勾配消失問題」というものがあります。これは、深い階層を持つニューラルネットワークを学習させる際に起こる問題です。ニューラルネットワークの学習では、出力側から入力側に向かって誤差を伝播させていくことで、より正確な結果を出せるように調整していきます。この誤差伝播の際に、層が深くなるにつれて勾配と呼ばれる数値がほぼゼロに近づいてしまい、学習がうまく進まなくなる現象が勾配消失問題です。誤差を伝える過程では、勾配を掛け算していくのですが、もし勾配の値が小さくなるような活性化関数を使っていると、この問題が起こりやすくなります。例えば、シグモイド関数という活性化関数は、勾配の最大値が0.25と小さいので、勾配消失問題を引き起こしやすい代表的な例として知られています。
問題の概要

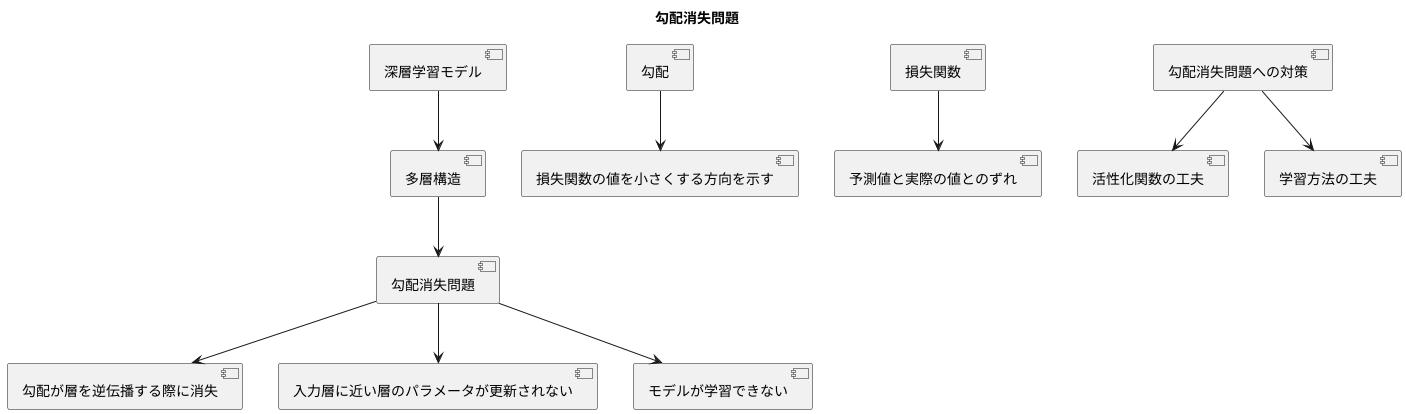
深層学習は、人間の脳の仕組みを模倣した多層構造を持つ学習モデルを用いることで、複雑な事象を学習できます。しかし、この多層構造が勾配消失問題と呼ばれる困難な課題を引き起こすことがあります。この問題は、特に層の数が多くなるほど顕著に現れます。
勾配消失問題は、学習の際に必要な情報がネットワークの層を逆伝播していく過程で徐々に薄れていく現象です。この学習に必要な情報は勾配と呼ばれ、損失関数の値を小さくする方向を示す重要な役割を担います。損失関数は、予測値と実際の値とのずれを表す指標であり、この値を小さくすることでモデルの精度を高めることができます。勾配は、この損失関数の値をどの程度、どの方向に調整すれば良いのかを示す道しるべのようなものです。
層の数が多い深いネットワークでは、この勾配が層を逆伝播するたびに小さくなってしまい、入力層に近い層に届く頃にはほとんど消えてしまいます。これは、ちょうど高い山の頂上から麓まで水が流れる間に、少しずつ水が地面にしみ込んでしまい、麓に届く頃にはほとんど水がなくなってしまう状況に似ています。
勾配が小さくなりすぎると、入力層に近い層のパラメータはほとんど更新されなくなります。パラメータはモデルの学習に不可欠な要素であり、これが更新されないということは、モデルが学習できないことを意味します。つまり、せっかく多くの層を重ねて複雑な事象を学習しようとしても、勾配消失問題によって学習が妨げられてしまうのです。
勾配消失問題は、深層学習における大きな壁の一つであり、この問題を解決するために様々な工夫が凝らされています。例えば、活性化関数の工夫や学習方法の工夫など、様々な手法が開発され、深層学習の発展に貢献しています。
発生の仕組み

学習をうまく進める上で重要なのが、誤差逆伝播法という手法です。これは、まるで川を遡上するように、出力層から入力層へと、誤差情報を伝えていくことで、各層の繋がり具合(重み)を調整する仕組みです。この調整によって、学習が進むにつれて、システム全体の予測精度が向上していくのです。
しかし、この誤差逆伝播法には、落とし穴があります。誤差を伝える過程で、活性化関数というものが重要な役割を果たします。活性化関数は、入力された情報を加工し、次の層へ伝えるための関数です。この活性化関数の微分値(関数の傾き)が、誤差の伝わり方に大きく影響します。
活性化関数の微分値が1よりも小さい場合、層が深くなるにつれて、誤差情報が薄れていくのです。これは、小さな数を何度も掛け合わせると、最終的にほぼゼロになってしまうのと同じ理屈です。層が深ければ深いほど、この現象は顕著になり、入力層に近い層には、ほとんど誤差情報が届かなくなります。これが、勾配消失問題と呼ばれる問題です。
勾配とは、簡単に言うと、学習の進み具合を表す指標のようなものです。勾配が小さければ小さいほど、学習は遅くなります。勾配消失問題では、入力層に近い層の勾配がほぼゼロになってしまうため、これらの層は学習が進まず、精度の向上に貢献できないのです。
例えば、以前はシグモイド関数という活性化関数がよく使われていました。しかし、シグモイド関数の微分値は最大でも0.25と小さいため、勾配消失問題を引き起こしやすいことが知られています。そのため、近年では、別の活性化関数が用いられることが多くなっています。
活性化関数と勾配消失

機械学習において、複雑なパターンを学習するために、ニューラルネットワークは複数の層を重ねて構成されます。この際、各層の出力を次の層の入力とする前に、活性化関数と呼ばれる変換を適用します。この活性化関数の選択が、学習の成否を大きく左右する重要な要素となります。特に、勾配消失問題と呼ばれる現象は、活性化関数の選択に密接に関連しています。
勾配消失問題は、ニューラルネットワークの学習において、誤差逆伝播法を用いて各層の重みを調整する際に発生します。誤差逆伝播法は、出力層における誤差を基に、各層の重みを修正していく手法です。この際、層が深くなるにつれて、誤差の値が小さくなっていく現象が勾配消失です。誤差が十分に伝播されなくなると、重みの更新が停滞し、学習がうまく進まなくなります。
従来よく用いられていたシグモイド関数は、入力値が大きい、あるいは小さい場合に、出力の変化が緩やかになる性質を持っています。この性質は関数の微分値が小さくなることを意味し、誤差逆伝播の過程で勾配が消失する原因となります。具体的には、シグモイド関数の微分値は最大でも0.25であり、層が深くなるにつれてこの値が繰り返し掛け合わされるため、勾配が急速に小さくなってしまいます。
こうした勾配消失問題に対処するために、近年では様々な活性化関数が開発されています。その代表例が、正規化線形関数、ReLUです。ReLUは、入力値が正の場合はそのまま出力し、負の場合は0を出力する関数です。入力値が正の場合、ReLUの微分値は常に1であるため、シグモイド関数のように勾配が小さくなることがありません。ReLUの導入により、多くの場合で勾配消失問題が軽減され、学習効率が向上することが確認されています。このように、活性化関数を適切に選択することで、ニューラルネットワークの学習を効率的に行うことが可能になります。
| 活性化関数 | 特徴 | 勾配消失問題 |
|---|---|---|
| シグモイド関数 | 入力値が大きい、あるいは小さい場合に出力の変化が緩やか 微分値は最大でも0.25 |
発生しやすい 層が深くなるにつれて勾配が急速に小さくなる |
| ReLU | 入力値が正の場合はそのまま出力、負の場合は0を出力 入力値が正の場合、微分値は常に1 |
発生しにくい 勾配が小さくなることがない |
問題への対策

人工知能の学習において、勾配消失問題は精度向上の大きな妨げとなります。これは、多層構造のネットワークで学習を進める際に、出力層から入力層へ向かう勾配の値が徐々に小さくなり、入力層に近い層のパラメータがほとんど更新されなくなってしまう現象です。この問題に対処するために、様々な対策が考え出されてきました。
まず、活性化関数の変更が有効な手段の一つです。従来よく使われていたシグモイド関数などは勾配消失問題を引き起こしやすい性質を持っていましたが、近年では、勾配消失問題の影響を受けにくいReLU関数などが広く利用されています。ReLU関数は、入力値が0以下の場合は常に0を出力し、正の値の場合はそのまま入力値を出力する関数です。
次に、重みの初期値を適切に設定することも重要です。初期値が不適切だと、学習がうまく進まないばかりか、勾配消失問題を悪化させる可能性もあります。適切な初期値の設定方法は様々ですが、一般的には小さな乱数で初期化することが推奨されています。
学習率の調整も重要な要素です。学習率が大きすぎると、パラメータの更新が不安定になり、最適な値に収束しにくくなります。逆に学習率が小さすぎると、学習に時間がかかりすぎたり、局所的な最適解に陥ってしまう可能性があります。
近年注目されているバッチ正規化も有効な対策です。これは、各層への入力を正規化することで、学習を安定させる手法です。入力値の分布を一定の範囲に収めることで、勾配消失問題の発生を抑える効果が期待できます。
さらに、ネットワークモデルの構造自体を変えるという方法もあります。LSTMやGRUといったモデルは、勾配消失問題に強い構造を持っており、時系列データの処理などに優れた性能を発揮します。
このように、勾配消失問題には様々な対策が存在します。問題の性質やデータの特性に合わせて、最適な対策を組み合わせることが重要です。
| 対策 | 説明 |
|---|---|
| 活性化関数の変更 | ReLU関数など、勾配消失問題の影響を受けにくい活性化関数を利用する。シグモイド関数などは勾配消失問題を引き起こしやすい。 |
| 重みの初期値設定 | 適切な初期値を設定することで、学習の効率化と勾配消失問題の悪化を防ぐ。一般的には小さな乱数で初期化することが推奨される。 |
| 学習率の調整 | 学習率が大きすぎるとパラメータ更新が不安定になり、小さすぎると学習に時間がかかり局所最適解に陥る可能性があるため、適切な値に調整する。 |
| バッチ正規化 | 各層への入力を正規化することで学習を安定させ、勾配消失問題の発生を抑える。 |
| ネットワークモデル構造の変更 | LSTMやGRUといった、勾配消失問題に強い構造を持つモデルを採用する。 |
深層学習への影響

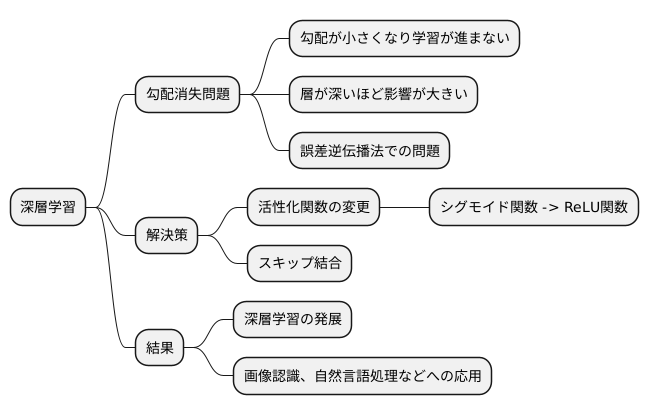
深層学習は、人間の脳の仕組みを模倣した学習方法で、多くの層を持つニューラルネットワークを用いることで複雑な事象を学習することができます。しかし、層を深く重ねるほど、学習の際に問題が生じることがありました。それが勾配消失問題です。
勾配とは、学習の進み具合を示す指標のようなもので、この勾配が小さくなりすぎてしまうと、学習がうまく進まなくなります。深い層を持つニューラルネットワークでは、出力層から入力層に向けて誤差を逆伝播させて学習を進めていくのですが、層が深くなるにつれて勾配がどんどん小さくなってしまい、入力層に近い層ではほとんど学習が進まなくなってしまうのです。これが勾配消失問題です。勾配消失問題は、深層学習の大きな壁となり、複雑な事象を学習できるはずの深層学習の力を十分に発揮できない原因となっていました。
この問題を解決するために、様々な対策が考案されました。その一つが、活性化関数の変更です。従来よく使われていたシグモイド関数などは、勾配消失問題を引き起こしやすい性質を持っていました。そこで、より勾配消失問題の影響を受けにくい「正規化線形関数」、通称ReLU関数が登場しました。ReLU関数は、入力値が0以下の場合は0を出力し、0より大きい場合はそのまま入力値を出力するという単純な関数ですが、勾配消失問題を軽減する効果があり、深層学習の発展に大きく貢献しました。
また、活性化関数の変更以外にも、様々な工夫が凝らされています。例えば、層を飛び越えて接続する「スキップ結合」といった手法も、勾配消失問題の軽減に効果的です。これらの対策によって、勾配消失問題の影響は大幅に軽減され、非常に深い層を持つニューラルネットワークの学習も可能になりました。
その結果、画像認識や自然言語処理など、様々な分野で深層学習が活用され、目覚ましい成果を上げています。今後も、勾配消失問題への対策手法の研究開発が進むことで、深層学習はさらに発展し、私たちの生活をより豊かにしてくれることが期待されます。
今後の展望

深層学習と呼ばれる技術は、人間の脳の仕組みを模倣した学習方法を用いて、様々な問題を解決できる可能性を秘めています。しかし、この学習の過程で「勾配消失問題」という壁に直面することがあります。これは、学習が進むにつれて、情報の伝達が薄れてしまい、学習の効果が弱まってしまう現象です。例えるなら、山の頂上を目指す登山家が、進むにつれて道が険しくなり、頂上に近づくほど一歩一歩の進みが遅くなってしまうようなものです。
この問題に対して、これまで多くの研究者が様々な対策を考案してきました。「ReLU」や「バッチ正規化」といった手法は、情報の伝達をスムーズにすることで、勾配消失問題をある程度解消することに成功しています。これらの手法は、登山道にロープや階段を設置するようなもので、より安全に頂上を目指せるようにしてくれます。しかし、現状ではまだ完璧な解決策は見つかっておらず、更なる改善が必要です。深層学習の技術は日々進歩しており、今後はさらに複雑なモデルが登場することが予想されます。複雑なモデルは、より高い山に登るようなもので、勾配消失問題の影響も大きくなると考えられます。そのため、より高度な対策が必要不可欠となるでしょう。
今後の研究では、情報の伝達効率をさらに高める新たな手法の開発が期待されています。例えば、新たな活性化関数の開発や、学習アルゴリズムの改良などが挙げられます。また、計算機の性能向上も重要な要素です。より高速な計算機は、複雑な計算を素早く処理できるため、学習の効率を高めることができます。これらの研究は、登山道具の改良や、登山ルートの開拓に例えることができ、深層学習の更なる発展に大きく貢献するでしょう。勾配消失問題の克服は、深層学習の進化、ひいては高度な人工知能の実現に向けて、今後も重要な課題であり続けるでしょう。
| 問題 | 説明 | 例え | 対策 | 対策の例え | 今後の課題 |
|---|---|---|---|---|---|
| 勾配消失問題 | 深層学習において、学習が進むにつれて情報の伝達が薄れ、学習効果が弱まる現象。 | 山の頂上を目指す登山家が、進むにつれて道が険しくなり、頂上に近づくほど一歩一歩の進みが遅くなる。 | ReLU、バッチ正規化などの手法 | 登山道にロープや階段を設置する |
|
