ReLU関数:深層学習の活性化関数

AIを知りたい
先生、ReLU関数ってなんですか?

AIエンジニア
ReLU関数は、人工知能の学習において、信号を伝えるか伝えないかを判断する役割を持つ関数の一つです。ゼロ以下の値はゼロとして扱われ、ゼロより大きい値はそのままの値として扱われます。例えば、入力信号が-2の場合は0に、5の場合は5になります。分かりやすく言うと、ランプのような形をした関数で、ランプ関数とも呼ばれます。

AIを知りたい
ランプのような形?ということは、途中で折れ曲がっているんですか?

AIエンジニア
その通りです。ゼロのところで折れ曲がっています。この性質によって、計算が簡単になり、コンピューターの負担を軽くすることができます。ただし、ゼロのところでは滑らかではないため、数学的には少し特殊な扱いが必要になります。それでも、ReLU関数は人工知能の学習を効率的に行う上で、とても重要な役割を果たしています。
ReLU関数とは。
『ランプ関数』とも呼ばれる『ReLU関数』について説明します。この関数は、人工知能に関連する用語です。
負の数が入力された場合は0を、0または正の数が入力された場合は入力された数と同じ数を返します。
この関数の特徴として、変化の割合の最大値が1と大きいことが挙げられます。変化の割合の最大値が小さい『シグモイド関数』のような他の活性化関数と比べると、勾配消失問題が起こりにくくなります。
また、計算が単純なので、計算にかかるコストも小さいです。
ただし、入力がちょうど0の場合は、関数がとぎれるため、微分できません。そのため、実際に使う場合は、便宜的に0や0.5、1などの値として扱います。
活性化関数には、ReLU関数の他にも多くの種類があります。中でも一番よく知られているのは『シグモイド関数』です。
活性化関数についてもっと詳しく知りたい場合は、実際にプログラムを動かせる記事があるので、そちらをご覧ください。(深層学習において重要なシグモイドやReLUなどの活性化関数の特徴を解説)
活性化関数とは

人間の脳の仕組みを参考に作られた人工知能の技術、深層学習では、活性化関数がとても大切な役割を担っています。
私たちの脳の中には、たくさんの神経細胞があります。これらの神経細胞は、他の神経細胞から信号を受け取ると、それを処理して次の神経細胞に伝えます。しかし、どんな小さな信号でも伝えるわけではありません。ある程度の強さの信号を受け取ったときだけ、次の神経細胞に信号を伝えます。この信号の強さを決めるのが、活性化関数です。
深層学習もこれと同じように、たくさんの層が重なってできています。それぞれの層では、前の層から受け取った情報をもとに計算を行い、次の層に情報を伝えます。このとき、活性化関数が、どの情報をどのくらい重要視するかを決めるのです。
活性化関数がないと、深層学習は複雑な問題をうまく処理できません。例えば、たくさんの層があっても、活性化関数がないと、それは1つの層と同じ働きしかできません。複雑な計算ができず、単純な計算しかできないということです。
活性化関数には、いくつか種類があります。よく使われるものとして、しきい値を0とするステップ関数、滑らかな曲線を描くシグモイド関数、ランプ関数とも呼ばれるReLU関数などがあります。それぞれに特徴があり、扱う問題によって使い分けられています。
つまり、活性化関数は、深層学習モデルの表現力を高めるために、なくてはならないものなのです。
| 項目 | 説明 |
|---|---|
| 深層学習 | 人間の脳の仕組みを参考に作られたAI技術。たくさんの層が重なってできている。 |
| 活性化関数 |
|
| 活性化関数の種類 | ステップ関数、シグモイド関数、ReLU関数など |
| 活性化関数がない場合 | 複雑な問題をうまく処理できない。複数の層があっても、1つの層と同じ働きしかできない。 |
ReLU関数の仕組み

ReLU関数は、「修正線形ユニット」と訳され、近年の深層学習で広く使われている活性化関数です。活性化関数とは、人工神経回路網において、入力信号をどの程度出力するかを調整する重要な要素です。ReLU関数は、その簡素さと効果から、多くのモデルで採用されています。入力値が0より大きい場合は、そのままの値を出力し、0以下の場合は0を出力するという、非常に単純な仕組みです。
たとえば、入力値が5の場合、出力も5です。入力値が-3の場合、出力は0になります。この動作をグラフに表すと、横軸が入力、縦軸が出力としたときに、原点で折れ曲がった直線となります。原点から右側の、入力値が正の部分は、傾き1の直線です。一方、原点から左側の、入力値が負の部分は、横軸に沿った水平線となります。
ReLU関数の大きな利点は、計算の手間が少ないことです。他の活性化関数、例えばシグモイド関数などは、指数計算などを含むため、計算に時間がかかります。ReLU関数は、単純な比較と値の選択だけで済むため、計算速度が大幅に向上します。これは、特に大規模なニューラルネットワークを扱う際に重要となります。
さらに、ReLU関数は、「勾配消失問題」と呼ばれる、深層学習における深刻な問題を軽減する効果も持っています。「勾配消失問題」とは、ネットワークの層が深くなるにつれて、学習に必要な情報である勾配が非常に小さくなってしまい、学習がうまく進まなくなる現象です。ReLU関数は、入力値が正の範囲では常に勾配が1であるため、この問題が起こりにくく、安定した学習を実現できます。これらの利点から、ReLU関数は、現在最も広く使われている活性化関数の1つと言えるでしょう。
ReLU関数の利点

活性化関数「修正線形ユニット」、略して「ReLU」には、色々な長所があります。その中でも特に注目すべき点は、計算の手軽さと、勾配消失問題への対策です。
まず、計算が手軽である点について説明します。ReLUは、入力が0より大きければそのまま出力し、0以下であれば0を出力するという単純な仕組みです。他の活性化関数、例えばシグモイド関数などは指数計算を含むため、計算に時間がかかります。それに比べてReLUは単純な比較と代入だけで済むため、計算にかかる時間が大幅に短縮できます。これは、学習時間の短縮に直結します。また、大規模なデータや複雑なモデルにも対応しやすくなるため、近年の深層学習の発展に大きく貢献しています。
次に、勾配消失問題への対策について説明します。勾配消失問題は、深層学習モデルの学習において、勾配が小さくなりすぎて学習が進まなくなる現象です。特に、シグモイド関数などでは、入力値が大きい、もしくは小さい場合に勾配が0に近づいてしまい、この問題が発生しやすくなります。ReLUでは、入力が0より大きい範囲では勾配が常に1であるため、勾配消失問題が生じにくく、安定した学習が可能になります。
これらの長所から、ReLUは現在、深層学習で最もよく使われている活性化関数のひとつとなっています。特に画像認識の分野では、ReLUを使うことで認識精度が向上したという報告が多くあります。ReLUの登場は、深層学習の進歩に大きく貢献したと言えるでしょう。
| 活性化関数ReLUの長所 | 説明 |
|---|---|
| 計算の手軽さ |
|
| 勾配消失問題への対策 |
|
ReLU関数の欠点と対策

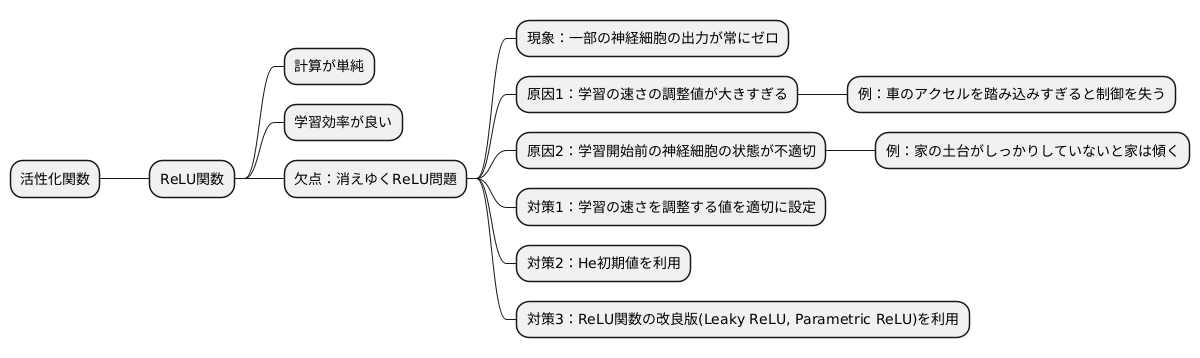
活性化関数とは、人工知能の学習において、まるで人間の脳神経細胞のように、入力された信号に応じて出力を調整する仕組みです。その中で、近年よく使われているのが「ReLU関数」です。ReLU関数は計算が単純で、学習の効率が良いという利点があります。しかし、ReLU関数には「消えゆくReLU問題」という欠点も存在します。
この「消えゆくReLU問題」とは、学習の過程で、一部の神経細胞の出力が常にゼロになってしまう現象です。ちょうど、電池が切れてしまったかのように、これらの神経細胞は学習に全く貢献できなくなってしまいます。そうなると、せっかく多くの神経細胞を用意していても、その一部が機能しなくなり、学習の精度が落ちてしまうのです。
この問題が発生する原因の一つに、学習の速さを調整する値の設定が挙げられます。この値が大きすぎると、学習の過程で修正が行き過ぎてしまい、神経細胞の出力がゼロになってしまうことがあります。ちょうど、車のアクセルを踏み込みすぎると、車が制御を失ってしまうようなイメージです。
また、学習を始める前の神経細胞の状態も重要です。適切な状態に設定されていないと、最初からうまく学習が進まず、神経細胞の出力がゼロになってしまう可能性があります。「家を建てる時の土台作り」と同じで、土台がしっかりしていないと、家は傾いてしまうように、学習の初期状態も適切に設定する必要があります。
この問題への対策としては、まず学習の速さを調整する値を適切に設定することが重要です。小さすぎると学習に時間がかかりすぎ、大きすぎると消えゆくReLU問題を引き起こすため、ちょうど良い値を見つける必要があります。また、「He初期値」と呼ばれる、ReLU関数に適した初期状態を利用することも有効です。これはReLU関数の特性に合わせて設計された初期状態で、学習開始時の神経細胞の状態を適切に設定できます。
さらに、ReLU関数の改良版である「Leaky ReLU」や「Parametric ReLU」なども開発されています。これらの改良版は、消えゆくReLU問題を回避するように設計されており、より安定した学習を実現できます。
このように、ReLU関数には欠点もありますが、適切な対策や改良版を用いることで、その欠点を克服し、効果的に人工知能の学習を進めることができます。
他の活性化関数との比較

様々な計算のやり方がある中で、情報のやり取りを調整する活性化関数には色々な種類があります。よく知られているものとしては、シグモイド関数、tanh(双曲線正接)関数、そしてReLU(正規化線形ユニット)関数などがあります。それぞれに特徴があり、どれを使うかは場合によって変わってきます。
まず、シグモイド関数は、0から1までの間の値を出力します。これは確率として解釈しやすいという利点があり、以前はよく使われていました。しかし、大きな値を入力すると、出力の変化が小さくなってしまうという性質があります。これは勾配消失問題として知られ、学習の速度が遅くなってしまう原因となります。
次に、tanh関数は、-1から1までの間の値を出力します。シグモイド関数と似ていますが、出力の中心が0であるため、勾配消失問題は少し軽減されます。しかし、シグモイド関数と同様に、大きな値を入力すると出力の変化が小さくなります。また、計算に時間がかかるという欠点もあります。
最後に、ReLU関数は、入力が0より小さい場合は0を、0以上の場合は入力と同じ値を出力します。計算が単純で速く、勾配消失問題も起こりにくいため、近年では最もよく使われている活性化関数です。ただし、入力が0より小さい時に出力が常に0になってしまうため、学習に悪影響を与える可能性もあります。これを改善するために、Leaky ReLUなど、様々な改良版が提案されています。
シグモイド関数、tanh関数、ReLU関数、それぞれに利点と欠点があります。目的や状況に応じて最適な活性化関数を選ぶことが、良い結果を得るためには重要です。近年では、より性能の高い活性化関数の研究開発も進んでおり、Swish関数など、新しい選択肢も増えています。
| 活性化関数 | 出力範囲 | 利点 | 欠点 |
|---|---|---|---|
| シグモイド関数 | 0 ~ 1 | 確率として解釈しやすい | 勾配消失問題、学習速度の低下 |
| tanh関数 | -1 ~ 1 | 出力の中心が0、勾配消失問題が軽減 | 勾配消失問題、計算に時間がかかる |
| ReLU関数 | 0 または x (x>=0) | 計算が単純で速い、勾配消失問題が起こりにくい | 入力が0より小さい時に出力が常に0 |
まとめ

情報を一つにまとめると、活性化関数のうち、修正線形ユニット(ReLU)関数は、近年の深い層を持つ学習モデルにおいて、なくてはならないものとなっています。その理由は、計算の手間が少なく済むこと、そして勾配消失問題と呼ばれる、学習の停滞をある程度抑えることができるためです。シグモイド関数や双曲線正接関数といった従来よく使われていた活性化関数に比べて、これらの点で優れているため、ReLU関数は広く用いられるようになりました。
しかしReLU関数にも弱点がないわけではありません。負の入力に対して出力が常にゼロになってしまう「死んだReLU問題」と呼ばれる問題が生じることがあります。これは、一部のニューロンが全く機能しなくなることを意味し、学習の効率を下げてしまう要因となります。この問題に対処するために、ReLU関数を改良した様々な派生形も提案されています。「漏洩ReLU関数」は、負の入力に対してもわずかな傾きを持たせることで、死んだReLU問題を軽減します。また、「パラメータ付きReLU関数」は、この傾きを学習によって最適化することで、より柔軟な表現を可能にします。
活性化関数の選択は、深い層を持つ学習モデルの性能を大きく左右する重要な要素です。ReLU関数は多くの利点を持つ一方で、死んだReLU問題といった欠点も抱えています。他の活性化関数、例えばシグモイド関数や双曲線正接関数、あるいはReLU関数の改良版なども含め、それぞれの特性を理解し、課題やモデルの構造に合わせて適切な活性化関数を選ぶことが、モデルの性能を最大限に引き出す鍵となります。活性化関数の仕組みを深く理解することで、より効果的な深い層を持つ学習モデルの設計と学習が可能になるでしょう。
| 活性化関数 | 利点 | 欠点 | 派生形 |
|---|---|---|---|
| ReLU関数 | 計算コストが低い、勾配消失問題を軽減 | 死んだReLU問題 | 漏洩ReLU関数、パラメータ付きReLU関数 |
| シグモイド関数 | 勾配消失問題 | ||
| 双曲線正接関数 | 勾配消失問題 | ||
| 漏洩ReLU関数 | 死んだReLU問題を軽減 | ||
| パラメータ付きReLU関数 | より柔軟な表現が可能 |
