虹色の強化学習:Rainbow

AIを知りたい
先生、「レインボー」って、たくさんの要素を組み合わせたすごい深層強化学習の手法だって聞きました。具体的にどんな要素を組み合わせているんですか?

AIエンジニア
いい質問だね!レインボーは7つの要素を組み合わせています。基本となるDQNに加えて、ダブルDQN、デュエリングネットワーク、マルチステップラーニング、ノイジーネットワーク、カテゴリカルDQN、そして優先度付き経験再生だよ。

AIを知りたい
7つもあるんですね!覚えるのが大変そうです…。それぞれの要素って、どんな役割を持っているんですか?

AIエンジニア
そうだね、たくさんあるから大変かもしれないけど、それぞれが学習を安定させたり、効率を良くする重要な役割を持っているんだ。例えば、ダブルDQNは過大評価を抑え、デュエリングネットワークは価値と利点を分けて学習するんだよ。他の要素もそれぞれ異なる役割を持っているから、興味があれば調べてみてね。
Rainbowとは。
人工知能に関わる言葉、『レインボー』について説明します。レインボーは二〇一七年に作られた、深く学ぶ強化学習という方法です。この方法は、深く学ぶ強化学習の基本的な方法であるDQNに加えて、いくつかの技術を組み合わせたものです。具体的には、二重DQN、競争ネットワーク、複数段階学習、ノイズを加えたネットワーク、分類DQN、優先順位をつけた経験再生の七つの要素をすべて合わせたものとなっています。結果として、レインボーはこれらの個々の要素を使った場合よりも高い性能を見せています。
虹色の構成要素

{虹のように美しい色の重なり合いを思い起こさせる「虹色」という名前を持つ深層強化学習の手法}についてお話しましょう。この手法は、まるで虹の七色が織りなす美しさのように、複数の要素を組み合わせることで、単独ではなしえない高い成果を生み出します。二〇一七年という、人工知能研究が大きく発展した年に開発されたこの手法は、七つの構成要素を巧みに組み合わせ、単独の要素を用いるよりも優れた性能を発揮します。
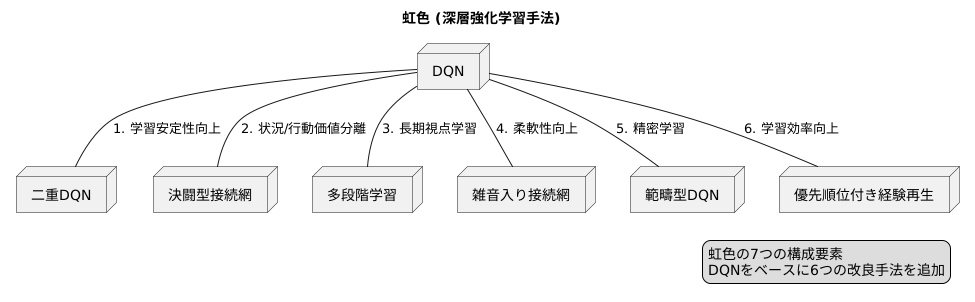
この手法の土台となっているのは、「DQN」と呼ばれる深層強化学習の基礎的な手法です。DQNは、ゲームの攻略などで成果を上げてきましたが、更なる改良を目指し、様々な改良手法が研究されてきました。虹色はこの流れを汲み、DQNに加え、六つの改良手法を取り入れることで、より高い学習能力を実現しています。
一つ目の改良手法は「二重DQN」と呼ばれ、学習の安定性を高める効果があります。二つ目は「決闘型接続網」で、これは状況の価値と行動の価値を分けて評価することで、より的確な判断を可能にします。そして三つ目は「多段階学習」です。これは、将来の報酬を予測することで、より長期的な視点での学習を実現します。
四つ目の「雑音入り接続網」は、学習にランダム性を取り入れることで、より柔軟な対応力を身につけます。五つ目の「範疇型DQN」は、行動の価値を確率分布として表現することで、より精密な学習を可能にします。そして最後の構成要素である「優先順位付き経験再生」は、過去の経験の中から重要なものを優先的に学習することで、効率的な学習を実現します。
これらの七つの要素が、虹色の鮮やかな性能の秘密です。それぞれの要素が持つ特性を組み合わせ、相乗効果を生み出すことで、単独では到達できない高度な学習を実現し、様々な課題を解決する可能性を秘めています。まるで虹の七色が一つに重なり合って美しい光を放つように、虹色もまた、七つの要素が調和することで、深層強化学習の新たな地平を切り開いていると言えるでしょう。
深層強化学習の基礎:DQN

深層強化学習は、人間の学習方法を模倣した機械学習の一種であり、試行錯誤を通じて学習を行う強化学習と、人間の脳の仕組みを模倣した深層学習を組み合わせた技術です。その中でも、DQN(ディープ・キュー・ネットワーク)は、深層強化学習の基礎となる重要な手法です。
DQNは、ゲームの画面を直接入力として受け取ることができます。例えば、テレビゲームの画面をピクセルデータとして入力し、その画面の状態に基づいて、どのボタンを押すべきかを判断します。従来の強化学習では、状態を数値で表現する必要がありましたが、DQNは深層学習を用いることで、画像などの複雑なデータから直接学習することが可能になりました。
DQNの学習は、試行錯誤を通じて行われます。ゲームをプレイしながら、様々な行動を試してみて、その結果に応じて報酬または罰則を受け取ります。例えば、ゲームで敵を倒せば報酬が与えられ、逆に敵にやられてしまえば罰則が与えられます。DQNは、この報酬と罰則の情報をもとに、将来の報酬を最大化するように行動を学習していきます。
DQNの核心部分は、行動価値関数と呼ばれるものを学習する点にあります。行動価値関数は、ある状態において、特定の行動をとった場合に、将来どれだけの報酬が得られるかを予測する関数です。DQNは、深層学習を用いてこの行動価値関数を近似的に表現します。そして、行動価値関数の予測値が最大となる行動を選択することで、最適な行動を決定します。
DQNは、Atariの様々なゲームで人間と同等、または人間を超える性能を達成し、深層強化学習の可能性を示しました。DQNは、その後の深層強化学習の発展に大きく貢献し、Rainbowなどのより高度な手法の土台となっています。DQNを理解することは、深層強化学習を学ぶ上で非常に重要です。
改良型DQN:DDQNとデュエリングネットワーク

深層強化学習の世界で、行動の価値を推定し、最適な行動を学習する手法の一つにDQN(深層Q学習)があります。DQNは画期的な手法でしたが、過大評価や学習の非効率性といった課題も抱えていました。そこで、これらの課題を解決するために、改良型のDQNがいくつか提案されました。本稿では、その中でも代表的な二つの改良型DQN、DDQN(二重DQN)とデュエリングネットワークについて解説します。
まず、DQNは行動価値を推定する際に、最大の行動価値を選択する傾向がありました。このため、実際よりも行動価値を高く見積もってしまう、つまり過大評価の問題が発生していました。DDQNはこの過大評価を抑えるために考案されました。DQNでは、行動価値の推定と行動の選択を同じネットワークで行っていましたが、DDQNでは二つのネットワークを用います。行動価値の推定は従来通り行いますが、行動の選択は別のネットワークを用いて行います。これにより、過大評価のリスクを軽減し、より正確な学習を可能にしています。
次に、デュエリングネットワークは、DQNの学習効率を向上させるために考案されました。DQNでは、各状態における各行動の価値を直接学習していました。一方、デュエリングネットワークでは、状態の価値と、各行動がもたらす追加の価値を別々に学習します。つまり、行動によって状態の価値が大きく変わらない場合でも、行動間の相対的な価値を効率的に学習できるようになります。具体的には、ネットワーク構造を二つの流れに分割し、一つは状態の価値、もう一つは行動の優位性を表す値を出力するように設計します。そして、これらを組み合わせることで、最終的な行動価値を計算します。
これらの改良型DQNは、DQNが抱えていた課題を克服し、深層強化学習の発展に大きく貢献しました。特に、これらの技術はRainbowなどのより高度な強化学習アルゴリズムの基礎となっており、様々な分野への応用が期待されています。
| 改良型DQN | 課題 | 解決策 | 効果 |
|---|---|---|---|
| DDQN (二重DQN) | DQNの過大評価 | 行動価値の推定と行動の選択を別々のネットワークで行う | 過大評価の軽減、より正確な学習 |
| デュエリングネットワーク | DQNの学習効率の低さ | 状態の価値と行動の優位性を別々に学習し、最後に統合 | 学習効率の向上、行動間の相対的な価値の効率的な学習 |
学習の効率化:マルチステップラーニングと優先度付き経験再生

近年の機械学習、特に強化学習の分野では、いかにして効率的に学習を進めるかが重要な課題となっています。膨大な試行錯誤を必要とする強化学習において、学習時間を短縮し、成果を最大化するための様々な手法が研究されています。その中でも、マルチステップラーニングと優先度付き経験再生は、特に注目されている二つの手法です。
まず、マルチステップラーニングについて説明します。従来の一歩先しか見ない学習方法では、遠い将来に得られる報酬の影響を理解するのに時間がかかります。例えば、囲碁で勝利するためには、一手一手の意味だけでなく、最終的な盤面の状態を見据えた戦略が必要です。マルチステップラーニングでは、数ステップ先の未来の報酬まで考慮することで、より長期的な視点に立った学習が可能になります。将来の報酬を予測しながら学習することで、より効率的に最適な行動を見つけ出すことができるのです。
次に、優先度付き経験再生について説明します。学習データは全て同じ価値を持つわけではありません。中には、学習に大きく貢献する重要な経験もあれば、そうでないものもあります。優先度付き経験再生は、過去の経験の中から、学習への影響が大きい重要な経験を優先的に選んで学習するという手法です。例えば、稀にしか起こらないが、大きな報酬や損失につながる経験は、学習にとって非常に重要です。このような重要な経験を優先的に学習することで、学習速度を向上させ、より効果的に学習を進めることができます。
マルチステップラーニングと優先度付き経験再生は、それぞれ異なるアプローチで学習の効率化を目指していますが、これらを組み合わせることで更なる効果が期待できます。遠い未来の報酬を考慮しつつ、過去の重要な経験から優先的に学習することで、限られた時間の中で最大限の学習効果を得ることができるのです。これらの手法は、強化学習の分野において革新的な進歩をもたらし、様々な応用分野で活用されています。
| 手法 | 説明 | メリット |
|---|---|---|
| マルチステップラーニング | 数ステップ先の未来の報酬まで考慮して学習する。 | 長期的な視点に立った学習が可能になり、効率的に最適な行動を見つけ出すことができる。 |
| 優先度付き経験再生 | 過去の経験の中から、学習への影響が大きい重要な経験を優先的に選んで学習する。 | 学習速度が向上し、より効果的に学習を進めることができる。 |
| マルチステップラーニングと優先度付き経験再生の組み合わせ | 遠い未来の報酬を考慮しつつ、過去の重要な経験から優先的に学習する。 | 限られた時間の中で最大限の学習効果を得ることができる。 |
探索能力の向上:ノイジーネットワーク

学習する人工知能は、まるで迷路を進む人のように、様々な行動を試しながらより良い結果を見つけようとします。しかし、常に最良と思われる選択だけをしていると、迷路の行き止まりに突き当たってしまうことがあります。これを局所最適解といいます。局所最適解とは、一見すると良い結果のように見えても、実際にはもっと良い結果が存在する状態です。
この問題を解決するために、人工知能の行動にわざと「ノイズ」、つまり「揺らぎ」を加える方法があります。これがノイジーネットワークと呼ばれる技術です。ノイズを加えることで、人工知能は普段とは異なる、思いがけない行動をとることがあります。迷路で例えるなら、いつもは右に曲がる場所を、ノイズによって左に曲がってみる、といった具合です。この「寄り道」が、より良い結果、つまり迷路の出口につながる可能性を広げるのです。
人工知能の一種であるレインボーは、このノイジーネットワークの考え方をうまく活用しています。レインボーは、ゲームの操作方法を学習する際、ノイズによって様々な操作を試します。これにより、最初は不器用に見えても、試行錯誤を通じてより効果的な操作方法を発見できます。まるで、新しいスポーツを始める初心者が、色々な動きを試しながら上達していく過程に似ています。
ノイジーネットワークは、人工知能が未知の領域を探索し、固定観念にとらわれずに新しい発見をするための重要な技術と言えるでしょう。この技術によって、人工知能は様々な課題を解決するための、より優れた方法を見つけ出すことができるようになるのです。
価値の分布を学習:カテゴリカルDQN

{ものの値打ちを一つに決めるのではなく、値打ちのばらつき具合を学習するのが、カテゴリカルディーキューエヌという考え方です。たとえば、ある行動をとったときに得られる点数を考えると、いつも同じ点数になるとは限りません。同じ行動でも、状況によって高い点数になったり低い点数になったりします。従来の方法では、この点数の一番ありそうな値だけを学習していました。しかし、カテゴリカルディーキューエヌでは、点数のばらつき具合全体を学習します。
具体的には、点数がどの範囲にどのくらいの確率で収まるのかを学習します。低い点数から高い点数まで、いくつかの区間に分けて、それぞれの区間にどのくらいの確率で点数が収まるのかを予測します。これにより、行動の結果にどれだけの不確実さが伴うのかを理解できます。たとえば、ある行動をとると高い点数が得られる可能性も低い点数が得られる可能性もそれなりにある場合と、確実に中くらいの点数が得られる場合では、意思決定の仕方が変わってきます。
不確実性を考慮することで、より賢い行動選択が可能になります。たとえば、確実に中くらいの点数が得られる行動と、高い点数が得られる可能性もあるが低い点数が得られる可能性もある行動があった場合、従来の方法では平均点が高いほうを選んでしまうかもしれません。しかし、低い点数が大きな痛手になる場合は、確実に中くらいの点数が得られる行動を選んだほうが良いでしょう。カテゴリカルディーキューエヌでは、このような状況でも適切な行動を選択できます。
レインボーという高度な学習方法は、このカテゴリカルディーキューエヌを取り入れることで、複雑で予測の難しい状況でも適切な行動を選択する能力を向上させています。様々な状況に対応できる、より柔軟で信頼性の高い学習方法と言えるでしょう。
| 項目 | 説明 |
|---|---|
| カテゴリカルDQN | ものの値打ちのばらつき具合を学習する考え方。行動の結果の点数だけでなく、その点数のばらつき(確率分布)を学習する。 |
| 従来の方法 | 行動の結果の点数の一番ありそうな値(平均値など)だけを学習。 |
| 学習方法 | 点数がどの範囲にどのくらいの確率で収まるのかを、いくつかの区間に分けて予測する。 |
| メリット | 行動の結果にどれだけの不確実さが伴うのかを理解し、より賢い行動選択が可能になる。 |
| 例 | 確実に中くらいの点数が得られる行動と、高い点数が得られる可能性もあるが低い点数が得られる可能性もある行動があった場合、低い点数が大きな痛手になる場合は、確実に中くらいの点数が得られる行動を選んだほうが良い。カテゴリカルDQNはこのような状況でも適切な行動を選択できる。 |
| レインボー | カテゴリカルDQNを取り入れた高度な学習方法。複雑で予測の難しい状況でも適切な行動を選択する能力を向上させる。 |
