Leaky ReLU関数: 改善された活性化関数

AIを知りたい
先生、「なめらかでないReLU関数」って、普通の「ReLU関数」と何が違うんですか?よくわからないです。

AIエンジニア
良い質問だね。普通の「ReLU関数」は、入力が0以下だと出力も0になってしまう。だから、学習の途中で一部の関数が全く働かなくなる「勾配消失」という問題が起こるんだ。そこで、「なめらかでないReLU関数」の出番だよ。

AIを知りたい
「なめらかでないReLU関数」だと、どうなるんですか?

AIエンジニア
入力が0以下のときも、ほんの少しだけ出力に反映させるんだ。そうすることで、「勾配消失」を防ぎ、学習を続けられるようにしているんだよ。だから、「ReLU関数」の弱点を補ったものと言えるね。
Leaky ReLU関数とは。
人工知能で使われる『リーキー・レル関数』について説明します。リーキー・レル関数は、活性化関数と呼ばれるレル関数の仲間です。レル関数は、ある程度、情報の伝わり方が弱くなる問題を防ぐことができます。しかし、入力値が0以下のときは、情報の伝わり方が完全に途絶えてしまい、うまく学習できないという欠点があります。この欠点を補うのが、リーキー・レル関数です。
活性化関数の役割

人間の脳を模倣した仕組みである人工知能は、その構成要素として神経細胞を真似た「ニューロン」と、ニューロン同士の繋がりである「シナプス」の働きを取り入れています。このニューロンとシナプスの繋がりを幾重にも重ねた構造が、人工知能の中核を担う「ニューラルネットワーク」です。このニューラルネットワークにおいて、活性化関数は各層のニューロンの出力を調整する重要な役割を担っています。
活性化関数の役割を理解するために、まずニューラルネットワークの構造を考えてみましょう。ニューラルネットワークは、入力層、中間層(隠れ層)、そして出力層から成り立っています。それぞれの層には複数のニューロンが存在し、前の層のニューロンからの信号を受け取り、次の層へと伝達していきます。この信号の伝達は、入力信号に重みを掛け合わせ、さらにバイアスと呼ばれる値を足し合わせるという計算によって行われます。しかし、この計算は掛け算と足し算という線形変換のみであるため、複雑な事象を学習するには不十分です。たとえ層を深く重ねたとしても、線形変換のみでは単一の層と変わらない単純な表現しかできません。
そこで登場するのが活性化関数です。活性化関数は、ニューロンの出力に非線形変換を加えることで、ネットワーク全体の表現力を飛躍的に向上させる働きをします。例えば、階段関数のように一定の値を超えたら1を出力し、それ以下なら0を出力するといった非線形変換を加えることで、ネットワークはより複雑なパターンを捉えることができるようになります。活性化関数を導入することで、単純な線形変換では表現できない、現実世界の問題を解くことが可能になるのです。
活性化関数の種類は多岐にわたり、それぞれ異なる特徴を持っています。代表的なものとしては、なめらかな曲線を描くシグモイド関数、0より大きい値ではそのまま値を返し、0以下では0を返すランプ関数、階段関数に似たステップ関数などがあります。どの活性化関数を選ぶかは、扱う問題の種類やネットワークの構造によって最適なものが異なり、学習の効率や最終的な性能に大きな影響を与えるため、慎重に検討する必要があります。
ReLU関数の登場と課題

これまで、人工神経回路網の活性化関数としては、主にシグモイド関数やハイパボリックタンジェント関数が用いられてきました。しかし、これらの関数には、層が深くなるにつれて学習効率が著しく低下する「勾配消失問題」という深刻な課題がありました。これは、誤差逆伝播法による学習において、層を遡るごとに勾配が小さくなり、やがて消失してしまう現象です。この問題により、深い層を持つ神経回路網の学習が困難になっていました。
このような状況を打開するために登場したのが、ReLU関数です。ReLU関数は、入力が正の値であればそのまま出力し、負の値であれば0を出力する、非常に単純な関数です。シグモイド関数やハイパボリックタンジェント関数に比べて計算量が少なく、処理速度が大幅に向上しました。また、正の入力に対しては勾配が常に1であるため、勾配消失問題もある程度軽減されるという利点がありました。これにより、以前は学習が難しかったより深い神経回路網の構築が可能になり、人工知能技術の発展に大きく貢献しました。
しかしReLU関数にも課題は存在します。入力が負の値の場合、出力は常に0となり、勾配も0になってしまいます。つまり、一度入力が負の値になると、そのニューロンは学習に全く寄与しなくなり、あたかも死んだように機能しなくなります。これは「死んだニューロン」と呼ばれ、ReLU関数の新たな課題として認識されています。この問題に対処するために、後に様々な改良型ReLU関数が提案されることになります。
| 活性化関数 | 特徴 | 利点 | 課題 |
|---|---|---|---|
| シグモイド関数 / ハイパボリックタンジェント関数 | 従来よく使われていた活性化関数 | – | 勾配消失問題により、深い層の学習が困難 |
| ReLU関数 | 入力が正ならそのまま出力、負なら0を出力 | 計算量が少ない、処理速度が向上、勾配消失問題を軽減 | 死んだニューロン問題(入力が負になると学習に寄与しなくなる) |
Leaky ReLU関数の仕組み

漏洩修正線形ユニット関数(リーキー・レルー)は、従来の修正線形ユニット関数(レルー)を改良した活性化関数です。活性化関数は、人工知能の学習において、データの流れを調整する重要な役割を担います。
従来のレルー関数は、入力値が0以上の場合はそのまま出力し、0未満の場合は0を出力します。これは、計算が単純で、学習速度も速いという利点がありました。しかし、入力値が0未満の場合、出力は常に0となり、学習が進まなくなる「死んだニューロン」と呼ばれる問題が発生することがありました。
この問題を解決するために開発されたのが、漏洩修正線形ユニット関数です。この関数は、入力値が0以上の場合は従来のレルー関数と同様にそのまま出力します。一方、入力値が0未満の場合は、入力値に非常に小さな正の値を掛けた値を出力します。この小さな正の値は、一般的に0.01などの値が用いられます。
この仕組みにより、入力値が0未満の場合でも、微小ながらも勾配が生じ、学習が継続されます。つまり、死んだニューロンの発生を抑制することができるのです。具体的には、入力値が負の領域でもわずかな傾きを持つ直線となり、これが「漏洩」を意味しています。
このように、漏洩修正線形ユニット関数は、従来のレルー関数の高速な処理という長所を維持しつつ、死んだニューロン問題という短所を克服することを目指した、より効果的な活性化関数と言えるでしょう。
| 活性化関数 | 入力値が0以上の場合 | 入力値が0未満の場合 | 利点 | 欠点 |
|---|---|---|---|---|
| ReLU (修正線形ユニット) | そのまま出力 | 0を出力 | 計算が単純、学習速度が速い | 死んだニューロン問題が発生する可能性がある |
| Leaky ReLU (漏洩修正線形ユニット) | そのまま出力 | 入力値に非常に小さな正の値(例:0.01)を掛けた値を出力 | ReLUの利点を維持、死んだニューロン問題を抑制 | – |
Leaky ReLU関数の利点

「漏れている修正線形関数」という聞きなれない名前の関数は、人工知能の分野で近年注目を集めている活性化関数の一つです。その名前の通り、従来よく使われていた「修正線形関数」を改良したもので、いくつかの点で優れています。
まず、「修正線形関数」を使う際に問題となっていたのが、一部の神経細胞が機能しなくなる「死んだ神経細胞」の問題です。これは、入力値が負になると関数の出力が常にゼロになり、学習が進まなくなる現象です。この問題に対し、「漏れている修正線形関数」は負の入力値に対してもわずかながら出力を持ち続けることで解決を図っています。小さな傾きを保つことで、負の入力値が来ても神経細胞は情報を伝達し続け、学習に貢献できるのです。すべての神経細胞が学習に参加することで、神経回路網全体の学習効率が向上します。
また、「漏れている修正線形関数」は「修正線形関数」と同様に計算の手間が少ないという利点も持っています。これは、大規模な神経回路網を扱う際に特に重要です。膨大な数の神経細胞が複雑に絡み合った神経回路網では、一つ一つの計算が単純であればあるほど全体の計算速度が向上し、学習にかかる時間を短縮できます。
これらの利点から、「漏れている修正線形関数」は画像認識や自然言語処理など、様々な分野で「修正線形関数」の代わりとして広く使われています。より精度の高い画像認識や、より自然な言葉の理解を実現するために、この「漏れている修正線形関数」が重要な役割を担っていると言えるでしょう。
| 項目 | 説明 |
|---|---|
| 関数名 | 漏れている修正線形関数 |
| 分野 | 人工知能、活性化関数 |
| 従来の問題点(修正線形関数) | 死んだ神経細胞問題:負の入力値で出力0、学習停止 |
| 改善点 | 負の入力値でもわずかな出力、学習継続、学習効率向上 |
| 利点 | 計算の手間が少ない、計算速度向上、学習時間短縮 |
| 応用分野 | 画像認識、自然言語処理など |
様々なReLU関数ファミリー

人工知能の分野において、活性化関数は神経細胞の働きを模倣する上で重要な役割を果たします。活性化関数の種類によって、学習の効率や精度が大きく変わることもあります。数ある活性化関数の中でも、近年注目を集めているのが、修正線形ユニット、いわゆる「ReLU」とその仲間たちです。
ReLUは、入力が正の値であればそのまま出力し、負の値であればゼロを出力するという単純な関数です。この単純さゆえに計算コストが低く、学習速度が速いという利点があります。しかし、入力が負の領域では常にゼロを出力するため、学習が進まない「勾配消失問題」が起こる可能性も孕んでいます。
この問題に対処するために、ReLUの改良版が数多く提案されてきました。その代表例が、「Leaky ReLU」です。Leaky ReLUは、入力が負の値の場合、小さな傾きを持つ直線で出力します。つまり、入力が負でもわずかながら値を伝えることで、勾配消失問題を軽減しようという工夫です。この小さな傾きは固定値として設定されることが一般的ですが、これを学習によって最適化するのが「Parametric ReLU」です。Parametric ReLUは、データに合わせて最適な傾きを自動的に学習することで、より柔軟な活性化を実現します。
さらに、「Randomized Leaky ReLU」では、この傾きをランダムに決定します。ランダム性を取り入れることで、過学習を抑え、より頑健なモデルを構築できる可能性があります。
このように、ReLU関数には様々な種類があり、それぞれに異なる特性があります。どの活性化関数が最適かは、扱うデータやモデルの構造によって異なります。状況に応じて適切なReLU関数を選択することで、より高い学習効果と精度の向上が期待できます。
| 活性化関数 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| ReLU | 入力が正ならそのまま出力、負なら0を出力 | 計算コストが低い、学習速度が速い | 勾配消失問題の可能性 |
| Leaky ReLU | 入力が負の場合、小さな傾きを持つ直線で出力 | 勾配消失問題の軽減 | 傾きが固定値 |
| Parametric ReLU | Leaky ReLUの傾きを学習によって最適化 | データに合わせて最適な傾きを学習 | – |
| Randomized Leaky ReLU | 傾きをランダムに決定 | 過学習の抑制、頑健なモデル構築の可能性 | – |
今後の展望

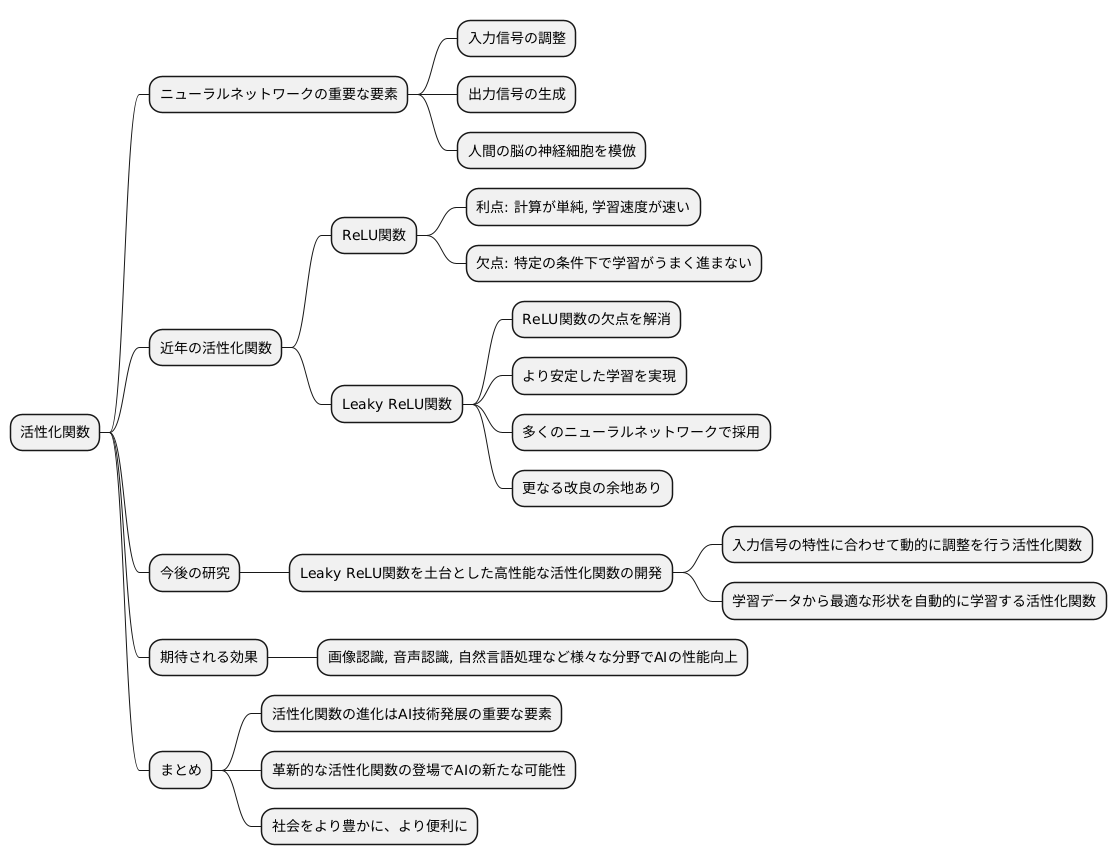
人工知能の中核をなす技術の一つであるニューラルネットワークは、活性化関数と呼ばれる重要な要素によってその性能が大きく左右されます。活性化関数は、入力信号を調整し、出力信号を生み出す役割を担っており、いわば人間の脳における神経細胞の働きを模倣したものです。そして現在、この活性化関数の研究は、世界中で活発に行われています。
近年、活性化関数としてよく用いられているのが、ReLU関数と呼ばれるものです。ReLU関数は、計算が単純で学習速度が速いという利点を持つ一方、特定の条件下では学習がうまく進まないという欠点も抱えていました。この欠点を克服するために開発されたのが、Leaky ReLU関数です。Leaky ReLU関数は、ReLU関数の問題点を解消し、より安定した学習を実現できるため、多くのニューラルネットワークで採用されています。しかし、Leaky ReLU関数も万能ではなく、更なる改良の余地が残されています。
そこで、今後の研究では、Leaky ReLU関数を土台として、より高性能な活性化関数の開発が期待されています。例えば、入力信号の特性に合わせて動的に調整を行う活性化関数や、学習データから最適な形状を自動的に学習する活性化関数などが考えられます。これらの新たな活性化関数が開発されることで、画像認識や音声認識、自然言語処理など、様々な分野における人工知能の性能が飛躍的に向上すると考えられます。
活性化関数の進化は、人工知能技術の発展を支える重要な要素です。今後、革新的な活性化関数が登場し、人工知能の新たな可能性を切り開くことが期待されます。そして、その進化は、私たちの社会をより豊かに、より便利に変えていく原動力となるでしょう。