画像を縮小:平均値プーリング

AIを知りたい
先生、「平均値プーリング」って、画像の大きさを小さくするんですよね?でも、ただ小さくするだけじゃなくて、何か特別なことをしているんですか?

AIエンジニア
そうだね、ただ小さくするだけではないんだ。例えば、2×2の正方形の枠を考えてみよう。この枠の中の4つの数を平均して、1つの数にする。これが平均値プーリングだよ。これを画像全体に繰り返すことで、画像を小さくしていくんだ。

AIを知りたい
なるほど。4つの数を平均するんですね。でも、なぜわざわざ平均するんですか?

AIエンジニア
いい質問だね。平均することで、画像が少しズレていても、プーリングの結果があまり変わらないようになるんだ。例えば、大切なものが画像の少し右側に写っていても、平均値プーリングのおかげで、その大切なものが認識できる可能性が高くなるんだよ。つまり、画像のズレに対して強くなる、言い換えれば頑健になるんだ。
平均値プーリングとは。
人工知能で使われる言葉、『平均値のまとめ方』について説明します。この『まとめ方』とは、画像の縦横の大きさを縮小する計算のことです。たとえば、縦横2つずつの小さな領域を決めて、その中の数値を一つにまとめます。平均値のまとめ方とは、まとめるときに、領域内の平均値を使う方法です。図で説明すると、4つの数字がある場合、それらを足し合わせて4で割った値を新しい値とします。普通は、まとめる領域の大きさと、その領域を動かす間隔は同じ値にします。このまとめる処理によって、画像が少しずれていても、正しく認識できるようになります。
平均値プーリングとは

平均値かたまり集めとは、絵の大きさを小さくする技術で、大切な模様を残しながら、処理を軽くする効果があります。これは、絵を細かい正方形のます目に分けて、それぞれのます目の色の濃さの平均を計算することで、新しい小さな絵を作る方法です。たとえば、2×2のます目に絵を分けると、四角の中の四つの点の色を足し合わせて四で割った値が、新しい絵のその部分の色になります。
この処理には、いくつか利点があります。まず、絵の情報量が減るので、後の処理が速くなります。たくさんの計算をしなくて済むので、計算機の負担を軽くできるのです。また、小さな色の違いや画像のざらざらしたノイズの影響を少なくする効果もあります。たとえば、少しだけ色が違う点がいくつかあっても、平均を取れば、その違いが目立たなくなります。これは、絵の模様を認識する作業などで、より正確な結果を得るのに役立ちます。
この方法は、細かいタイルを敷き詰めた絵を遠くから見ることに似ています。近くで見ると一つ一つのタイルの違いがよく分かりますが、遠くから見ると、細かい違いは分からなくなり、全体的な模様だけがはっきりと見えてきます。平均値かたまり集めも同様に、細かい情報を取り除くことで、絵の大切な特徴を際立たせる効果があるのです。このため、物の形を見分けるといった作業に役立ち、人工知能の分野で広く使われています。
| 項目 | 説明 |
|---|---|
| 技術名 | 平均値かたまり集め |
| 目的 | 絵の大きさを小さくし、処理を軽くする |
| 手法 | 絵を正方形のます目に分け、各ます目の色の平均値を計算し、新しい絵を作る |
| 例 | 2×2のます目の場合、4つの点の色の合計を4で割る |
| 利点1 | 情報量が減り、処理速度が向上 |
| 利点2 | ノイズの影響を軽減 |
| 利点3 | 絵の大切な特徴を際立たせる |
| 応用例 | 物の形を見分ける、人工知能 |
| アナロジー | タイルを敷き詰めた絵を遠くから見る |
計算方法

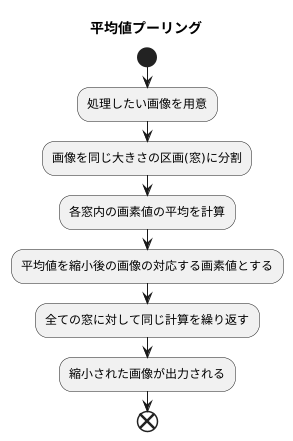
計算方法はとても分かりやすいです。まず、処理したい画像を同じ大きさの区画に分けていきます。この区画のことを窓と呼び、その大きさは窓の大きさであらかじめ決めておきます。たとえば、窓の大きさを縦と横2つずつと決めた場合、元の画像は縦と横それぞれ2つずつの正方形の区画に分けられます。
次に、各窓の中にある画素の値の平均を計算します。画素とは、画像を構成する最小単位の点で、それぞれの色情報を持っています。たとえば、一つの窓の中に4つの画素があり、それぞれの値が10、12、15、18だとします。この場合、平均値は(10+12+15+18)÷4=13.75となります。
この平均値が、縮小後の画像の対応する場所の画素の値になります。つまり、もとの画像の4つの画素の情報が、新しい画像では一つの画素に凝縮されるわけです。すべての窓に対して同じ計算をすることで、元の画像よりも小さな画像が作られます。
この計算方法を平均値プーリングと呼びます。平均値プーリングは、画像の情報をギュッと縮めることで、データの量を減らし、処理を速くすることができます。また、画像の中の小さな変化の影響を少なくし、重要な特徴を捉えやすくする効果もあります。たとえば、手書きの数字を認識する場合、少し線がずれていても同じ数字として認識できるようにするために、この方法がよく使われています。
移動間隔

画像認識などで、全体を少しずつずらして見たい時に、どのくらいの間隔でずらすのかを考える必要があります。このずらす間隔を移動間隔と言い、移動間隔の大きさは処理の速度や結果に大きく影響します。移動間隔のことを専門用語でストライドとも呼びます。
例えば、正方形の窓枠を通して画像を見ているとしましょう。この窓枠の大きさが2×2だとします。そして、この窓枠を動かしながら画像全体をくまなく見ていくことを考えます。この時、窓枠を動かす間隔が移動間隔です。
一般的には、窓枠の大きさと移動間隔を同じ値に設定することが多いです。例えば、窓枠の大きさが2×2で、移動間隔も2に設定した場合、窓枠はぴったりと2画素ずつ移動します。つまり、窓枠同士が重なる部分はなく、画像全体を効率よく見ることができます。この場合、元の画像の大きさに対して、窓枠を通して見た画像は約半分の大きさになります。
もし、移動間隔を1に設定するとどうなるでしょうか。この場合、窓枠は1画素ずつ移動することになります。すると、窓枠同士が大きく重なることになり、結果として窓枠を通して見た画像は元の画像の大きさとほぼ同じ大きさになります。一見、細かく見ているので良いように思えますが、窓枠を動かす回数が増えるため、処理にかかる時間が長くなってしまいます。
このように、移動間隔を適切に設定することはとても大切です。移動間隔を大きくすると、処理速度は速くなりますが、画像の特徴を見落とす可能性があります。反対に、移動間隔を小さくすると、処理速度は遅くなりますが、画像の特徴をより細かく捉えることができます。そのため、処理速度と得られる情報のバランスを考えて、適切な移動間隔を選ぶ必要があります。
| 移動間隔 | 窓枠の重なり | 処理速度 | 特徴の捕捉 | 画像サイズ |
|---|---|---|---|---|
| 大きい(例: 窓枠サイズと同じ) | なし | 速い | 見落とす可能性あり | 約半分 |
| 小さい(例: 1) | 大きい | 遅い | より細かく捉える | ほぼ同じ |
画像のズレへの対応

{写真の位置がずれてしまう}という問題への対策として、平均値寄せ集めという手法がよく用いられています。この手法は、写真の中で位置が多少ずれていても、全体的な特徴を捉えることができるため、ずれに対して強いという利点があります。
例えば、手書きの数字を認識する場合を考えてみましょう。同じ数字であっても、書き方や位置は人によって微妙に異なります。しかし、平均値寄せ集めを使うと、これらの小さなずれの影響を少なくすることができます。これは、写真の一部分を寄せ集めることで、小さなずれは平均化され、数字全体の特徴がより明確になるためです。
具体的には、写真の小さな領域(例えば、縦横2×2の正方形)を一つにまとめる処理を考えます。この小さな領域の中で色の濃さを平均することで、一つの代表値を得ることができます。この処理を写真全体に繰り返すことで、写真の解像度は下がりますが、ずれやノイズの影響を減らすことができます。
手書き文字認識の例で言えば、「3」という数字の書き始め位置が少し上にずれていても、平均値寄せ集めによって、そのずれは他の部分と混ざり合い、「3」の特徴として捉えることができます。
このように、平均値寄せ集めは、写真のずれに対して強いという特性から、写真認識における重要な下準備として広く活用されています。特に、手書き文字認識や物体検出など、位置のずれが問題となるタスクにおいて、その効果は顕著です。
また、平均値寄せ集めは計算も比較的簡単であるため、処理速度の面でも利点があります。大量の写真データを扱う場合でも、高速に処理できるため、実用的な手法と言えるでしょう。
| 手法 | 説明 | 利点 | 用途 |
|---|---|---|---|
| 平均値寄せ集め | 写真の小さな領域(例:2×2ピクセル)の色の濃さを平均し、一つの代表値にする処理を写真全体に繰り返す。 | 写真のずれやノイズの影響を軽減 計算が比較的簡単で処理速度が速い |
手書き文字認識 物体検出 位置のずれが問題となるタスク |
応用例

平均値プーリングは、画像を扱う様々な場面で活用されています。その応用例をいくつか見ていきましょう。まず、画像認識の中でも特に画像分類の分野では、畳み込みニューラルネットワーク(CNN)の一部として平均値プーリングが重要な役割を果たしています。畳み込み層で抽出された沢山の特徴の中から、重要な部分をより分けて取り出し、データの大きさを小さくすることで、次の処理をスムーズに進める助けとなっています。
物体検出の分野でも、平均値プーリングは力を発揮します。写真の中に写っているものが何であるかだけでなく、そのものが写真のどのあたりにあるのかを大まかに特定する際に役立ちます。例えば、写真に猫が写っている場合、猫がいるおおよその場所を四角い枠で囲むといった処理で利用されます。
また、画像の見た目に関する処理にも平均値プーリングは効果があります。写真に写り込んだ不要な点や線などのノイズを取り除き、画像をより綺麗に、鮮明に見やすくする効果があります。
医療の分野でも、平均値プーリングは活躍しています。レントゲン写真やMRI画像といった医療画像を解析する際に、病気によって変化した体の部分を見つけ出すのに役立っています。これにより、医師の診断を支援し、より正確な診断へと繋げることが期待されています。
このように、平均値プーリングは様々な分野で利用されており、複雑な計算を必要としないシンプルな仕組みながらも、画像処理において高い効果を発揮します。このことから、今後さらに多くの分野で活用されていくと考えられます。
| 分野 | 平均値プーリングの役割 |
|---|---|
| 画像分類 | 畳み込みニューラルネットワーク(CNN)の一部として、重要な特徴をより分け、データの大きさを小さくする。 |
| 物体検出 | 写真の中に写っている物体が何であるかと、そのものの写真のどのあたりにあるのかを大まかに特定する。 |
| 画像ノイズ除去 | 写真に写り込んだ不要な点や線などのノイズを取り除き、画像をより綺麗に、鮮明に見やすくする。 |
| 医療画像解析 | レントゲン写真やMRI画像といった医療画像を解析する際に、病気によって変化した体の部分を見つけ出す。 |
他のプーリング手法との比較

画像認識の分野では、プーリングと呼ばれる手法が広く使われています。プーリングは、画像データのサイズを小さくすることで、計算量を減らし、過学習を防ぐ役割を担っています。様々なプーリング手法の中で、平均値プーリングは、注目領域内の画素値の平均値を取り出すというシンプルな方法です。この手法は、画像にノイズが含まれる場合に効果を発揮します。ノイズは、本来の画像情報とは異なる余計な情報であり、平均を取ることでノイズの影響を薄めることができるからです。例えば、少しノイズの入った滑らかな濃淡の変化を捉えたい時に、平均値プーリングはなめらかな変化を保ったままノイズの影響を軽減できます。
一方、最大値プーリングは、注目領域内の画素値の最大値を取り出す手法です。これは、画像の中で最も目立つ特徴を捉えるのに役立ちます。例えば、画像にエッジ(境界線)のようなはっきりとした特徴が含まれる場合、最大値プーリングはそのエッジを強調し、他の細かい情報を捨てることで、特徴を際立たせます。しかし、平均値プーリングに比べて、情報の損失が大きくなる可能性がある点に注意が必要です。重要な情報が失われてしまうと、画像認識の精度が低下する可能性があります。
平均値プーリングと最大値プーリング以外にも、最小値プーリングや中央値プーリングといった手法も存在します。最小値プーリングは、注目領域内の画素値の最小値を取り出し、中央値プーリングは、画素値を大きさの順に並べた時に中央に位置する値を取り出します。しかし、これらの手法は平均値プーリングと最大値プーリングほど広く使われていません。
どのプーリング手法を選ぶかは、扱う画像データの特性や、画像認識の目的に合わせて適切に判断する必要があります。ノイズが多い画像には平均値プーリング、明確な特徴を捉えたい場合は最大値プーリングが適していると言えるでしょう。それぞれの特性を理解し、最適な手法を選択することで、より効果的な画像認識を行うことができます。
| プーリング手法 | 説明 | 利点 | 欠点 | 適した場面 |
|---|---|---|---|---|
| 平均値プーリング | 注目領域内の画素値の平均値を取り出す。 | ノイズの影響を軽減できる。滑らかな変化を保つ。 | – | ノイズが多い画像 |
| 最大値プーリング | 注目領域内の画素値の最大値を取り出す。 | 画像の中で最も目立つ特徴を捉える。エッジを強調。 | 情報の損失が大きくなる可能性がある。 | 明確な特徴を捉えたい場合 |
| 最小値プーリング | 注目領域内の画素値の最小値を取り出す。 | – | – | – |
| 中央値プーリング | 画素値を大きさの順に並べた時に中央に位置する値を取り出す。 | – | – | – |
