軽量畳み込みで高速化

AIを知りたい
『Depthwise Separable Convolution』って、通常の畳み込み処理と比べて何が違うんですか?

AIエンジニア
いい質問だね。『Depthwise Separable Convolution』は、通常の畳み込み処理を2つのステップに分解することで計算量を減らす工夫なんだ。まず、それぞれの色の層ごとに別々に畳み込み処理を行い、次に、色の層を混ぜ合わせるように畳み込み処理を行うんだよ。

AIを知りたい
色の層ごとに別々に処理するんですね。でも、それだと普通の畳み込みと結果が違うくなりませんか?

AIエンジニア
たしかに、全く同じ結果にはならない。でも、計算量を大幅に削減できるメリットの方が大きい場合も多いんだ。特に、モバイル端末のように計算資源が限られている環境では有効な手法だよ。
Depthwise Separable Convolutionとは。
『奥行き分離畳み込み』という人工知能の用語について説明します。奥行き分離畳み込みは、モバイルネットという技術で使われている、通常の畳み込み処理の代わりに用いられる画像処理の方法です。
入力画像の大きさを縦×横×奥行きで表すと、例えば縦×横がN×N、奥行きがWとします。通常の畳み込み処理では、M個の縦×横×奥行きがK×K×Wのフィルターを使います。
一方、奥行き分離畳み込みでは、まずK×Kのフィルターを使って、奥行き方向に畳み込み処理を行います。その後、M個の1×1×Wのフィルターを使って、縦方向と横方向に畳み込み処理を行います。
このように処理を変えることで、計算量が約8分の1にまで減りました。
処理の仕組み

奥行き方向分離可能畳み込みと呼ばれる処理は、通常の畳み込み処理と比べて、計算の手間を大幅に減らすことができます。この処理の仕組みを詳しく見ていきましょう。
まず、通常の畳み込み処理では、入力画像の色の層全てに対して、一度に畳み込み処理を行います。たとえば、入力画像の大きさが縦にN画素、横にN画素、色の層の数がWの場合、M個のK×K×Wサイズのフィルターを使います。つまり、フィルターの奥行きは入力画像の色の層の数と同じになります。このため、計算量が多くなってしまいます。
奥行き方向分離可能畳み込みでは、この畳み込み処理を、空間方向と色の層の方向に分けて行うことで、計算量を減らします。まず、それぞれの色の層に対して、K×Kサイズのフィルターを個別に適用します。この処理を奥行き方向畳み込みと呼びます。それぞれの層を独立に処理することで、計算を効率化できます。
次に、1×1×WサイズのフィルターをM個使って、色の層の方向に畳み込み処理を行います。この処理を点状畳み込みと呼びます。これは、異なる色の層からの情報を混ぜ合わせる役割を果たします。
このように、奥行き方向畳み込みと点状畳み込みの二段階に分けて処理を行うことで、フィルターのサイズを小さくでき、結果として通常の畳み込み処理よりも計算量を大幅に削減できるのです。これは、特に携帯端末などの計算資源が限られた環境では大きな利点となります。
| 処理 | フィルターサイズ | 説明 |
|---|---|---|
| 通常の畳み込み | K×K×W | 入力画像の色の層全てに対して、一度に畳み込み処理を行います。 |
| 奥行き方向畳み込み | K×K | それぞれの色の層に対して、K×Kサイズのフィルターを個別に適用します。 |
| 点状畳み込み | 1×1×W | 色の層の方向に畳み込み処理を行い、異なる色の層からの情報を混ぜ合わせます。 |
計算量の削減効果

画像認識などでよく使われる畳み込み処理は、多くの計算を必要とします。例えば、入力画像の大きさをN×N、畳み込みフィルターの大きさをK×K、入力のチャンネル数をW、出力のチャンネル数をMとすると、従来の畳み込み処理に必要な計算量はN×N×K×K×W×Mとなります。これは、フィルターを画像全体に適用していくため、計算量が大きくなってしまうのです。
そこで、計算量を減らす工夫として、Depthwise Separable Convolutionという手法が登場しました。この手法は、畳み込み処理を二つの段階に分けます。一つ目はDepthwise Convolutionと呼ばれるもので、これはそれぞれの入力チャンネルに対して別々のフィルターを適用します。この時の計算量はN×N×K×K×Wとなります。二つ目はPointwise Convolutionと呼ばれるもので、これは1×1のフィルターを使って、それぞれの位置でチャンネル方向の情報を組み合わせます。この時の計算量はN×N×W×Mとなります。
Depthwise Separable Convolutionの全体の計算量は、Depthwise ConvolutionとPointwise Convolutionの計算量の合計、つまりN×N×K×K×W+N×N×W×Mとなります。例えば、フィルターの大きさが3×3(K=3)で、入力と出力のチャンネル数が同じ(M=W)場合を考えてみましょう。従来の畳み込み処理の計算量を基準にすると、Depthwise Separable Convolutionの計算量は約8分の1になります。これは、フィルターの適用範囲を限定することで、計算量を大幅に削減できることを示しています。
このような計算量の削減は、処理速度の向上に直接つながります。特に、スマートフォンやタブレットなどの計算資源が限られた機器では、この効果は非常に重要です。Depthwise Separable Convolutionを使うことで、限られた資源でも高速な画像認識などが可能になります。
| 手法 | 計算量 | 説明 |
|---|---|---|
| 従来の畳み込み | N×N×K×K×W×M | フィルターを画像全体に適用 |
| Depthwise Convolution | N×N×K×K×W | 各入力チャンネルに別々のフィルターを適用 |
| Pointwise Convolution | N×N×W×M | 1×1フィルターでチャンネル方向の情報を結合 |
| Depthwise Separable Convolution | N×N×K×K×W + N×N×W×M | Depthwise ConvolutionとPointwise Convolutionの合計 |
モバイルネットにおける活用

携帯電話などの移動端末向けのネットワーク技術であるモバイルネットは、限られた処理能力と電力で効率的に動作する必要があります。そこで、計算量を削減しつつ高い精度を維持する技術が重要になります。この課題を解決する手段の一つとして、モバイルネットでは「分離可能な畳み込み」と呼ばれる手法が中心的に用いられています。
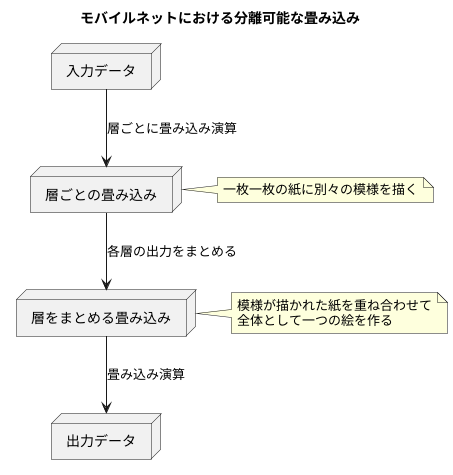
従来の畳み込み処理は、入力データの全ての層に対して一度に畳み込み演算を行うため、計算負荷が大きくなります。一方、分離可能な畳み込みは、この処理を二つの段階に分けて行います。「層ごとの畳み込み」と「層をまとめる畳み込み」です。まず、層ごとの畳み込みでは、入力データの各層に対して個別に畳み込み演算を行います。これは、一枚一枚の紙に別々の模様を描くようなものです。次に、層をまとめる畳み込みでは、前段階で処理された各層の出力をまとめて、一つの畳み込み演算を行います。これは、模様が描かれた紙を重ね合わせて、全体として一つの絵を作るようなものです。
このように処理を分けることで、従来の畳み込み処理に比べて計算量を大幅に削減できます。処理が軽くなるため、モバイルネットのような限られた計算資源しかない環境でも、高速な画像認識や物体検出といった処理が可能になります。例えば、写真に写っている物体が何かを瞬時に判断したり、動画中の物体の動きを滑らかに追跡したりすることができるようになります。
モバイルネットは、この分離可能な畳み込みを効果的に活用することで、処理速度と精度のバランスを最適化し、移動端末での様々な応用を実現しています。今後も、モバイルネットの進化に伴って、分離可能な畳み込み技術も更に発展していくと考えられます。
精度の維持

深層学習モデルにおいて、計算の効率化は処理速度の向上や省電力化に欠かせません。しかし、効率化を進めるあまり、モデルの精度が低下してしまうと、本来の目的を果たせなくなってしまいます。計算量を減らしつつも精度を保つことは、常に重要な課題となっています。その解決策の一つとして、Depthwise Separable Convolution(分離可能畳み込み)という手法が注目されています。
この手法は、通常の畳み込み処理を二つの段階に分けて行います。まず、Depthwise Convolution(奥行き方向畳み込み)では、入力画像の各チャンネルごとに独立したフィルターを適用します。次に、Pointwise Convolution(点ごとの畳み込み)では、1×1のフィルターを用いて、前の段階で得られた複数のチャンネルの出力を組み合わせて新たな特徴マップを生成します。
この二段階の処理によって、通常の畳み込みに比べて計算量を大幅に削減できます。通常の畳み込みでは、全てのチャンネルが一度に処理されるため、計算量が大きくなってしまうからです。一方、分離可能畳み込みでは、チャンネルごとに独立して処理を行うため、計算量を抑えることができます。
計算量を削減しても、精度は維持できるのでしょうか? 実は、分離可能畳み込みは、適切に設計することで、通常の畳み込みと同程度の精度を維持できます。具体的には、フィルターの大きさや点ごとの畳み込みにおけるチャンネル数を調整することで、精度を維持しつつ計算量を削減することが可能です。例えば、MobileNetと呼ばれる軽量な深層学習モデルでは、この分離可能畳み込みが効果的に活用されており、限られた計算資源でも高い精度を実現しています。
このように、分離可能畳み込みは、計算の効率化と精度の維持の両立を目指す上で、非常に有効な手法と言えるでしょう。今後の深層学習モデルの設計においても、重要な役割を担っていくことが期待されます。
今後の展望

計算資源の制約が大きな課題となっている近年において、処理能力の向上と省資源化の両立は大変重要です。このような状況下で、計算量を削減しつつも高い精度を維持できる手法として注目されているのが、分離可能畳み込みと呼ばれる技術です。この技術は、今後の様々な分野での活用が期待されています。
特に、機器の小型化や低消費電力化が求められる、いわゆる「物のインターネット」と呼ばれる分野や、現場に近い場所でデータ処理を行う「エッジコンピューティング」と呼ばれる分野においては、その効果が顕著に現れると考えられています。これらの分野では、利用できる計算資源が限られているため、従来の畳み込み演算のような計算量の多い処理は大きな負担となっていました。分離可能畳み込みを用いることで、限られた計算資源でも高度な画像認識や音声処理などの機能を実現できる可能性が広がります。
現在、分離可能畳み込み以外にも、計算の効率を高めるための様々な研究開発が行われています。例えば、畳み込み演算における不要な計算を省いたり、計算の順序を工夫したりすることで、更なる高速化や省電力化を目指した取り組みが活発に進められています。また、限られた計算資源でも高い精度を達成できるような、新しい演算方法の開発も期待されています。
これらの技術革新は、今後ますます多くの機器で高度な処理を可能にするでしょう。例えば、スマートフォンや家電製品などの身近な機器から、自動車の自動運転システムや医療機器などの専門性の高い機器まで、幅広い分野への応用が期待されます。分離可能畳み込み技術をはじめとする様々な研究開発の進展により、私たちの生活はより便利で豊かになるでしょう。より少ない資源でより多くのことを実現できる未来が、すぐそこまで来ていると言えるでしょう。
| 課題 | 解決策 | 応用分野 | 期待される効果 |
|---|---|---|---|
| 計算資源の制約 | 分離可能畳み込み 畳み込み演算の効率化 新しい演算方法の開発 |
IoT エッジコンピューティング スマートフォン 家電製品 自動車の自動運転システム 医療機器 |
処理能力向上 省資源化 機器の小型化 低消費電力化 高度な画像認識・音声処理 生活の利便性向上 |
適用範囲の拡大

奥行き方向分離畳み込み(Depthwise Separable Convolution)は、元々は画像の認識といった分野で活用されていましたが、近頃では、言葉の処理や音の認識など、他の様々な分野にも応用されるようになってきています。これらの分野においても、計算の手間を減らしつつ、認識の正確さを維持できるという利点が評価されています。
たとえば、言葉の処理では、文章の意味を理解するモデルに利用されています。従来の手法に比べて、奥行き方向分離畳み込みを使うことで、計算の手間を大幅に減らし、処理速度を向上させることが可能になります。また、音の認識では、音声データから特徴を抽出する部分に利用されています。音声データは一般的にデータ量が大きいため、計算の手間が問題となりますが、この技術を用いることで効率的に処理することが可能になります。
奥行き方向分離畳み込みの利点は、計算の手間を減らせることにあります。これは、通常の畳み込みでは全ての層が繋がっているのに対し、奥行き方向分離畳み込みでは層を分離して計算を行うためです。それぞれの層を個別に処理することで、計算量を大幅に削減できます。さらに、パラメータ数も少なくなるため、モデルの軽量化にも繋がります。
精度の維持という点も重要な利点です。計算の手間を減らす一方で、認識の正確さを損なわないことが重要です。奥行き方向分離畳み込みは、層を分離することで計算量を削減しますが、それぞれの層で重要な特徴を抽出するため、精度の低下を抑えることが可能です。
今後、奥行き方向分離畳み込みはさらに様々な分野への応用が期待されています。様々な形式のデータにも適用できる可能性があり、研究開発が進められています。今後、この技術がさらに発展し、様々な分野で活用されることで、人工知能技術の進歩に大きく貢献することが期待されます。
| 項目 | 内容 |
|---|---|
| 技術名 | 奥行き方向分離畳み込み(Depthwise Separable Convolution) |
| 従来の応用分野 | 画像認識 |
| 近年の応用分野 | 言葉の処理、音の認識など |
| 利点 | 計算の手間を減らしつつ、認識の正確さを維持できる。モデルの軽量化。 |
| 言葉の処理での利用例 | 文章の意味を理解するモデル |
| 言葉の処理での効果 | 計算の手間を大幅に減らし、処理速度を向上 |
| 音の認識での利用例 | 音声データから特徴を抽出 |
| 音の認識での効果 | データ量の大きい音声データを効率的に処理 |
| 計算の手間削減の理由 | 層を分離して計算を行うため、計算量を大幅に削減。パラメータ数も減少。 |
| 精度の維持の理由 | 層を分離しても、それぞれの層で重要な特徴を抽出するため。 |
| 今後の展望 | 様々な形式のデータへの適用、人工知能技術の進歩への貢献 |
