信用割当問題と誤差逆伝播法

AIを知りたい
先生、『信用割当問題』って、複雑な計算をしているたくさんの部品の中で、どの部品がどれくらい役に立っているのか分からなくなる問題だってことですよね?

AIエンジニア
そうだね。たくさんの部品、つまりたくさんの『パラメータ』がどのように影響しているのかわからなくなる、という問題だね。例えば、たくさんの人が共同で作った巨大な絵があるとしよう。絵の出来栄えが悪かったときに、誰のせいで悪いのか、また誰の腕を磨けば絵が良くなるのかが分からない、という状況に似ているよ。

AIを知りたい
なるほど。では、どうやってその問題を解決するのですか?

AIエンジニア
巨大な絵の例でいうと、完成した絵と理想の絵を比べて、まず絵全体の悪かった点を明らかにする。それから、その悪かった点が誰の担当部分に由来するのかを一人ずつ調べていくような方法で解決するんだ。AIの世界では『誤差逆伝播法』と呼ばれる方法で、出力に近い部分から入力に近い部分へと、順番に各パラメータの影響を調べていくことで解決しているんだよ。
信用割当問題とは。
人工知能にまつわる言葉で「どの部分がどれだけ役に立っているのか」を知る方法について説明します。
人工知能はたくさんの部品がつながってできており、まるで脳の神経細胞のようです。
そして、人工知能に何かを学習させるときには、それぞれの部品がどれくらい役に立っているのか、また、どの部品をどのように調整すればもっと賢くなるのかが、すぐには分かりませんでした。これは「信用をどのように割り当てるか」という問題、つまり「信用割当問題」と呼ばれていました。
しかし、今では、答え合わせをして間違いを計算し、その間違いがどこから来たのかを部品ごとに調べていく方法が見つかりました。これは、まるで間違いを矢印のように部品に沿って送り返していくような方法で、「誤差逆伝播法」と呼ばれています。この方法のおかげで、「信用割当問題」は解決されました。
はじめに

人間の頭脳の仕組みを真似た技術である人工知能の中核を担う神経回路網は、まさに脳の神経細胞がつながる様子を模した構造を持ち、学習を重ねることで複雑な課題を解き明かすことができます。しかし、この学習の過程において、それぞれの構成要素がどのように予測や判断に役立っているのかを理解することは容易ではありませんでした。これは、どの要素がどれほど結果に影響を与えているのかを特定するのが難しいという、長年の課題であり、信用割当問題として知られています。
この問題は、まるでチームで仕事をした後、誰の貢献がどれほど大きかったのかを正確に評価するような難しさに例えられます。もし個々の貢献度が分からなければ、適切な報酬や改善点を示すことができません。神経回路網も同様に、どの部分がうまく機能し、どの部分が改善を必要とするのかを理解できなければ、効果的な学習は望めません。そこで登場するのが、誤差逆伝播法という画期的な解決策です。
誤差逆伝播法は、出力された結果と正解との間の誤差を、出力層から入力層に向かって逆向きに伝えることで、各要素の貢献度を計算します。これは、最終的な成果から逆算して、それぞれの段階での貢献度を明らかにするようなものです。チームの仕事で例えるなら、最終的な成果物から、各メンバーの作業内容を振り返り、それぞれの貢献度を評価するようなものです。
近年の深層学習、つまり多層構造を持つ神経回路網の発展は、この誤差逆伝播法の登場によるところが大きいと言えます。誤差逆伝播法によって、複雑な神経回路網でも効率的に学習を進めることができるようになり、人工知能技術は飛躍的な進歩を遂げました。この技術は、画像認識や音声認識、自然言語処理など、様々な分野で応用され、私たちの生活にも大きな影響を与えています。まさに誤差逆伝播法は、人工知能の発展を支える重要な柱と言えるでしょう。

信用割当問題とは

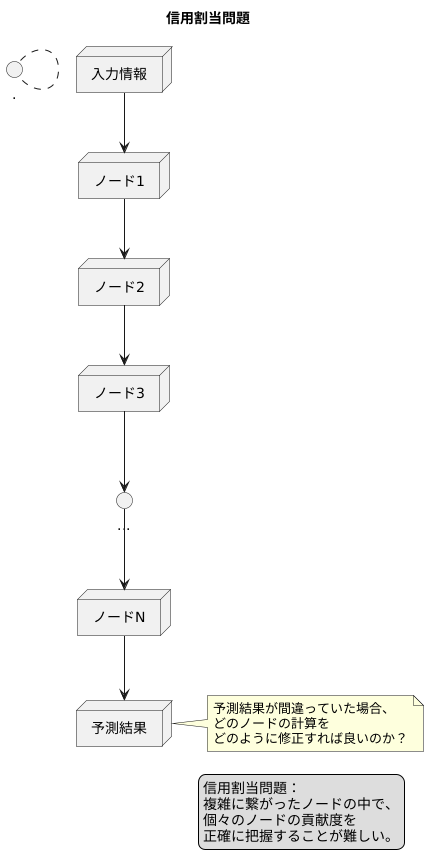
信用割当問題とは、人間の脳の神経細胞を模したたくさんの小さな計算機、つまりノードが複雑につながり合った構造を持つニューラルネットワークという仕組みにおいて、学習をうまく進める上で壁となる難しい問題です。この仕組みは、入力された情報がそれぞれのノードを順番に経由して処理され、最後に答えとなる予測結果を出すようにできています。しかし、この予測結果が間違っていた場合、どのノードの計算の仕方をどのように修正すれば正解に近づけることができるのかを特定するのが非常に困難なのです。これが信用割当問題と呼ばれるものです。
ニューラルネットワークは、幾重にも重なった層の中で、無数のノードが互いに複雑に繋がっています。それぞれのノードは、前の層から受け取った情報を計算し、次の層へと渡していきます。この複雑なネットワークの中で、最終的な予測結果にどのノードがどれだけの影響を与えているかを正確に把握することは至難の業です。例えるなら、巨大な組織の中で、それぞれの社員の働きが最終的な業績にどれほど貢献しているかを正確に評価するようなものです。それぞれの社員の仕事ぶりは他の社員と密接に関連しており、個々の貢献度を分離して評価することは非常に難しいでしょう。
ニューラルネットワークも同様に、個々のノードの貢献度を正確に測ることができないため、どのノードの計算の仕方をどのように修正すれば良いのかが分からず、学習の効率が落ちてしまいます。まるで、たくさんの人が力を合わせて作った料理の味を良くするために、誰の作ったどの部分が改善すべきか分からず、闇雲に試行錯誤するようなものです。適切な修正個所が分からなければ、いつまで経っても美味しい料理は作れません。信用割当問題は、ニューラルネットワークの学習を効率的に進める上で、このノードの貢献度をどのように評価するかという重要な課題を突きつけているのです。
誤差逆伝播法の登場

多くの層が積み重なった複雑な仕組みの中で、どの部分が最終的な結果にどれくらい影響を与えているかを正確に把握することは、調整を行う上で非常に重要です。しかし、複雑に絡み合ったネットワーク構造の中で、各構成要素の責任の所在を特定することは容易ではありません。これを信用割当問題と呼んでいます。
この難題を解決する革新的な方法として、誤差逆伝播法が登場しました。この手法は、完成品に見られる誤差を、最終工程から出発して、各工程を逆順にたどりながら、その誤差がどのように発生したかを分析していく方法です。
具体的には、まず最終工程における完成品の誤差を数値化します。そして、各工程間のつながりの強さを表す数値を用いて、前の工程にどれだけの誤差が由来するかを計算します。例えるなら、最終製品の不良品率から、各部品の不良率を逆算するようなものです。
この計算を繰り返すことで、初期の工程に至るまで誤差の伝播を調べることができ、各工程における調整の必要性を数値的に把握できます。ちょうど、最終製品の不具合の原因を特定するために、製造工程を一つずつ遡って検査していくようなイメージです。
誤差逆伝播法によって、複雑なネットワークの各部分の貢献度を効率よく計算できるようになり、学習の速度と精度が飛躍的に向上しました。以前は職人技に頼っていた調整作業を、数値に基づいて行うことができるようになったため、より精緻で効率的な改善が可能になりました。この手法は、現代の人工知能技術の根幹を支える重要な技術の一つと言えるでしょう。
誤差逆伝播法の仕組み

誤差逆伝播法は、学習機械の分野で広く使われている手法で、複雑な計算構造を持つ学習機械の調整を可能にします。この手法は、連鎖律と呼ばれる数学の法則を巧みに利用しています。連鎖律とは、複数の関数が入れ子になっている場合、全体の変化量をそれぞれの関数の変化量の積で表せるという法則です。
学習機械は、入力を受け取り、何層もの計算を経て結果を出力します。それぞれの層には、計算を調整するための色々な数値が用意されています。これらの数値を適切に調整することで、学習機械の性能を高めることができます。しかし、複雑な学習機械では、調整すべき数値と最終結果の関係が分かりにくいという問題があります。
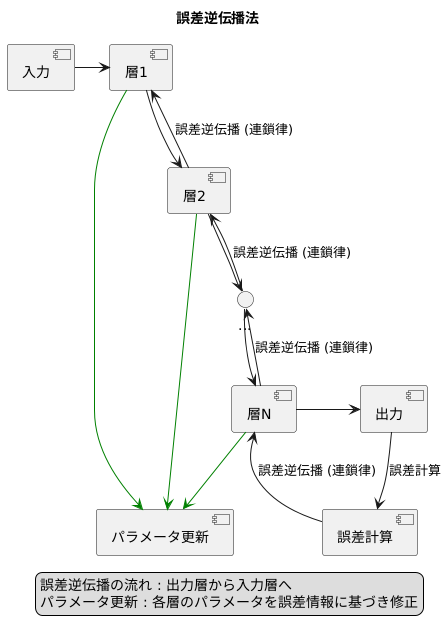
ここで、誤差逆伝播法が役立ちます。学習機械の最終結果と、目標とする結果との差を誤差と呼びます。この誤差を小さくすることが学習機械の目標です。誤差逆伝播法は、連鎖律を使って、各層の数値が最終的な誤差にどの程度影響を与えているかを計算します。具体的には、出力層から入力層に向かって、各層の数値が誤差に与える影響を順次計算していきます。
この計算は、ちょうど水が上から下へ流れるように、出力層から入力層へと伝わるため、「逆伝播」と呼ばれます。各層の計算では、その層の出力がどのように計算されるかと、その計算に使われる数値が用いられます。こうして得られた、各数値が誤差に与える影響の度合いを使って、数値を適切に修正することで、誤差を小さくすることができます。つまり、学習機械の性能を高めることができるのです。この一連の流れが、誤差逆伝播法の仕組みです。
誤差逆伝播法の意義

誤差逆伝播法は、人工知能の分野、特に機械学習において、画期的な学習手法として知られています。この手法が登場する以前は、多層構造を持つ複雑なニューラルネットワークの学習は非常に困難でした。これは、出力層で発生した誤差を、どのようにして入力層に近い層へと伝達し、各層の結合の重みを適切に修正すれば良いのか、その方法が分からなかったからです。言い換えれば、学習の指針となる適切な方法が見つかっていなかったのです。
誤差逆伝播法は、この問題を解決する画期的な手法でした。この手法は、微分という数学の概念を利用して、出力層で発生した誤差を、ネットワークの各層に逆方向へ伝播させ、各層の結合の重みを効率的に修正する方法を提供します。まるで鎖のようにつながった層全体に、誤差の影響を適切に分配することで、ネットワーク全体の学習を効率的に行うことができるようになったのです。
この誤差逆伝播法の登場により、多層構造を持つ複雑なニューラルネットワークの学習が可能になり、人工知能研究は大きな進展を遂げました。画像認識や音声認識、自然言語処理といった様々な分野において、精度の高い認識や予測が可能となり、人工知能技術の実用化が急速に進みました。今日、私たちが目にする人工知能技術の多くは、誤差逆伝播法の恩恵を受けていると言っても過言ではありません。深層学習(ディープラーニング)と呼ばれる、さらに多層化したニューラルネットワークの学習においても、誤差逆伝播法は中核的な役割を担っており、人工知能技術の発展に欠かせない存在であり続けています。まさに、誤差逆伝播法は、人工知能の扉を開く重要な鍵となったのです。
| 手法 | 課題 | 解決策 | 効果 |
|---|---|---|---|
| 誤差逆伝播法 | 多層ニューラルネットワークの学習における、出力層誤差の入力層への伝達と重み修正方法の欠如 | 微分を利用して出力層誤差を各層に逆伝播、重みを効率的に修正 | 多層ニューラルネットワーク学習の実現、画像認識・音声認識・自然言語処理等の精度向上、人工知能技術の実用化、深層学習の中核技術 |
今後の展望

誤差逆伝播法は、人工知能の学習を大きく前進させた画期的な手法です。この手法は、まるで生物の神経回路網のように、入力データから出力結果を得るまでの過程を模倣し、その過程で生じた誤差を各層にフィードバックすることで学習を進めます。しかし、この強力な手法にも、まだいくつかの課題が残されています。
まず、勾配消失問題と呼ばれる現象があります。これは、多層構造を持つネットワークを学習させる際に、誤差情報が層を遡るにつれて徐々に薄れてしまい、入力層に近い層のパラメータがうまく調整できなくなる問題です。ちょうど、高い山の頂上から麓まで水が流れ落ちる際に、途中で水が涸れてしまうようなイメージです。この問題は、ネットワークの層数を深くするほど顕著になり、複雑なタスクを学習する際の大きな障壁となっています。
また、膨大な計算資源と学習データを必要とする点も課題です。近年のコンピュータ技術の進歩は目覚ましいものがありますが、それでも誤差逆伝播法を用いた学習には、莫大な時間と電力が必要となります。特に、画像認識や自然言語処理といった複雑なタスクでは、より多くのデータと計算資源が必要となり、容易には解決できない問題となっています。まるで、広大な土地を耕すのに、多くの時間と労力を要するようなものです。
これらの課題を解決するために、様々な研究が行われています。勾配消失問題に対しては、活性化関数の工夫や学習率の調整といった手法が提案されています。また、計算資源の問題に対しては、より効率的なアルゴリズムの開発や、計算を分散処理する技術の研究が進められています。これらの研究の進展により、今後、より強力で効率的な学習手法が実現すると期待されます。人工知能技術の更なる進化は、まさにこれらの課題を克服した先にあると言えるでしょう。
| 課題 | 説明 | 例え | 対策 |
|---|---|---|---|
| 勾配消失問題 | 多層構造のネットワークで、誤差情報が層を遡るにつれて薄れ、入力層に近い層のパラメータがうまく調整できなくなる問題。 | 高い山の頂上から麓まで水が流れ落ちる際に、途中で水が涸れてしまう | 活性化関数の工夫、学習率の調整 |
| 膨大な計算資源と学習データ | 誤差逆伝播法を用いた学習には、莫大な時間と電力が必要。特に、画像認識や自然言語処理といった複雑なタスクでは、より多くのデータと計算資源が必要。 | 広大な土地を耕すのに、多くの時間と労力を要する | より効率的なアルゴリズムの開発、計算を分散処理する技術の研究 |
