誤差逆伝播法：学習の鍵

誤差逆伝播法：学習の鍵

はじめに

人の知恵を模した技術である人工知能の世界では、機械学習というものが近年、驚くほどの進歩を見せています。中でも、人の脳の仕組みをまねたニューラルネットワークは、写真を見て何が写っているかを判断したり、人の言葉を理解したりといった様々な仕事で、素晴らしい成果を上げています。

このニューラルネットワークをうまく働かせるためには、重みと呼ばれる大切な数値を適切に調整する必要があります。ちょうど、料理の味を調えるために、塩や砂糖の量を少しずつ変えていくように、重みの値を調整することで、ニューラルネットワークの精度を高めていくのです。

この重みを効率よく調整する方法の一つが、誤差逆伝播法と呼ばれるものです。この方法は、まるで迷路を解くように、目標とのズレを少しずつ修正しながら、最適な重みの値を探し出すことができます。複雑に絡み合ったネットワークでも、この方法を使えば、一つ一つの重みをどのように調整すれば良いのかが分かります。

誤差逆伝播法は、今日の深層学習と呼ばれる技術の進歩に大きく貢献しています。深層学習は、何層にも積み重なった複雑なニューラルネットワークを使うことで、より高度な問題を解決することを可能にします。この複雑なネットワークを学習させるためには、効率的な重みの調整が不可欠であり、誤差逆伝播法はその重要な役割を担っているのです。

誤差逆伝播法は、人工知能の発展を支える重要な技術と言えるでしょう。今後、さらに高度な人工知能を実現するためにも、誤差逆伝播法の理解はますます重要になっていくと考えられます。

多層パーセプトロンの学習

多層パーセプトロンは、人間の脳の神経回路網を模倣した学習モデルです。このモデルは、入力層、一つ以上の隠れ層、そして出力層という複数の層から構成されています。それぞれの層には、ノードと呼ばれる処理単位が複数存在し、これらのノードは層を跨いで複雑に繋がっています。

学習の過程を見ていきましょう。まず、入力層にデータが入力されます。この入力データは、各ノード間の繋がりを介して次の層へと伝達されます。この繋がりには、それぞれ重みと呼ばれる数値が割り当てられています。この重みは、入力データの影響度合いを調整する役割を果たします。データは、入力層から隠れ層、そして出力層へと順に伝達され、最終的に出力層から予測値が出力されます。

この予測値と、実際に得られた値との差が誤差です。学習の目的は、この誤差を出来るだけ小さくすることです。誤差を小さくするために、各ノード間の重みを調整する必要があります。この調整は、出力層から入力層に向かって、誤差を逆向きに伝播させることで行います。この手法は、誤差逆伝播法と呼ばれ、多層パーセプトロンの学習において重要な役割を担っています。従来の学習方法と比較して、誤差逆伝播法は、重みの調整を効率的に行うことが可能です。これにより、複雑な問題に対しても、高い精度で予測を行うことができます。多層パーセプトロンと誤差逆伝播法の組み合わせは、画像認識や音声認識など、様々な分野で応用されています。

誤差逆伝播法の仕組み

誤差逆伝播法は、多層の神経回路網における学習方法であり、出力層から入力層に向かって誤差を戻していくという、一見不思議な方法で重みの調整を行います。目的は、神経回路網の予測値と実際の値との間のずれ、すなわち誤差を最小にすることです。

まず、学習のために用意したデータを使って神経回路網に予測をさせます。この時、出力された予測値と正解となる値との差を計算します。これが誤差です。この誤差を出力層から入力層に向かって順に伝播させていきます。

誤差の伝播は、鎖の法則に基づいて計算されます。鎖の法則とは、複数の関数を通して値が変化する時、全体の変化量を各関数の変化量の積で表せるという法則です。神経回路網では、各層の計算が関数に相当し、誤差がこの関数を通して伝播していきます。各層では、伝播してきた誤差と、その層の活性化関数の微分値を用いて、重みを調整します。活性化関数の微分値は、その層の入力が変化した時に出力がどれだけ変化するかを表すもので、重みの調整量を決めるために必要です。

誤差を伝える際に、各層の重みに対する影響度を計算します。これは、重みを少し変化させた時に誤差がどれだけ変化するかを表すもので、勾配と呼ばれます。この勾配情報を利用して、誤差を減らす方向に重みを調整します。つまり、勾配が大きい重みは大きく調整され、勾配が小さい重みは小さく調整されます。

このように、誤差逆伝播法は、出力層から入力層へ誤差を伝播させながら、各層の重みを調整していくことで、神経回路網全体の誤差を最小化し、精度の高い予測を可能にします。

勾配降下法との関係

誤差逆伝播法は、勾配降下法を多層構造の認識機に適用した手法です。この手法を理解するには、まず勾配降下法の仕組みを理解する必要があります。勾配降下法とは、ある関数の最小値を見つけるための計算手法です。山を下ることに例えると、現在地から最も急な斜面を下ることで、谷底、つまり最小値にたどり着くことができます。この最も急な斜面の方向は、関数の勾配によって示されます。

認識機学習では、誤差関数と呼ばれる関数が重要な役割を担います。この関数は、認識機の予測と実際の値とのずれを表しており、このずれが小さいほど、認識機の性能が良いことを示します。つまり、認識機学習の目的は、この誤差関数を最小にすることです。

ここで、勾配降下法が登場します。誤差関数の最小値を見つけるために、誤差関数の勾配を計算します。この勾配は、誤差関数を最小にするための最も急な下り坂の方向を示しています。そして、この勾配に基づいて、認識機の重みと呼ばれる変数を調整します。重みは、認識機の予測に影響を与える重要な要素であり、この重みを適切に調整することで、誤差を減らすことができます。

誤差逆伝播法は、この勾配を効率的に計算する手法です。多層構造の認識機では、計算が複雑になりがちですが、誤差逆伝播法は、出力層から入力層に向かって、順次勾配を計算していくことで、効率的に勾配を求めることができます。このように、誤差逆伝播法は、勾配降下法を用いて重みを最適化し、誤差関数を最小にすることで、認識機の性能を向上させる手法と言えるでしょう。

深層学習への応用

深層学習とは、人間の脳の神経回路を模倣したニューラルネットワークを多層構造にしたもので、複雑な事柄を学習する能力を持つ仕組みです。この学習をうまく行うために、誤差逆伝播法という手法が重要な役割を担っています。

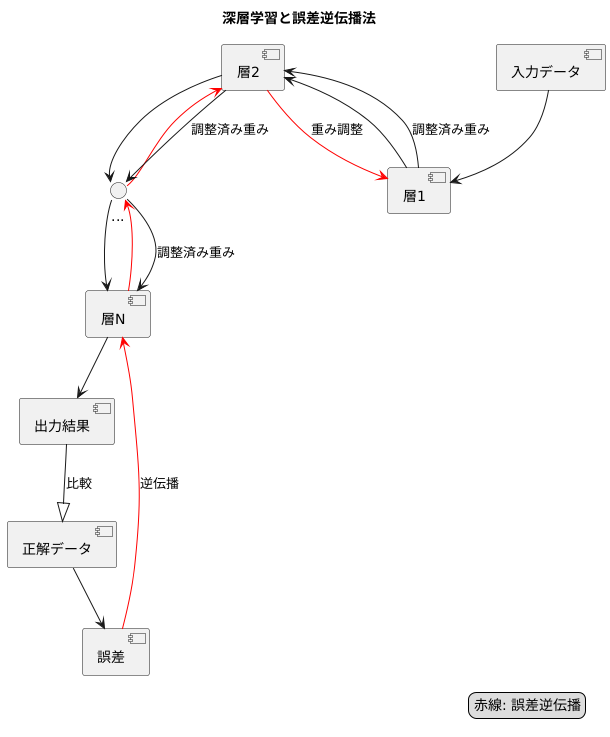
深層学習では、入力データから出力結果を得るまで、何層もの計算の段階を経ます。それぞれの層にはたくさんの繋がりの強さ（重みと呼ばれる数値）があり、この重みを調整することで学習を行います。層の数が増えれば増えるほど、重みの数は膨大になり、まるで巨大な迷路の中で最適な道を探すような、非常に難しい問題となります。

誤差逆伝播法は、この複雑な迷路を解くための巧みな方法です。まず、学習データを使って計算を行い、出力結果と正解データとの違い（誤差）を調べます。そして、この誤差を最後の層から最初の層へと逆向きに伝えていくことで、それぞれの層の重みが誤差にどの程度影響を与えているかを計算します。この計算結果に基づいて、誤差を小さくするように重みを少しずつ調整していくのです。

誤差を逆向きに伝えていく様子が、まるで川を遡上するかのようであることから、「逆伝播」という名前が付けられました。この方法のおかげで、膨大な数の重みを持つ深層学習でも、効率的に学習を進めることが可能になりました。

近年では、この誤差逆伝播法をさらに改良した手法も数多く開発されています。例えば、誤差を伝える際に、一部の情報だけを伝達したり、伝達する量を調整したりすることで、より速く、より正確に学習できるようになりました。こうした技術の進歩が、深層学習の更なる発展を支えていると言えるでしょう。

まとめ

誤差逆伝播法は、人間の脳の神経回路網を模した仕組みであるニューラルネットワークの学習には欠かせない重要な計算手法です。この手法は、学習の際に、出力された結果と正解データとの間の誤差を、出力側から入力側へと逆方向に伝播させることで、各層の結合の強さを調整します。

具体的には、まず、ニューラルネットワークに学習データを入力し、出力結果を得ます。次に、この出力結果と正解データとの差、つまり誤差を計算します。そして、この誤差をネットワークの出力側から入力側へと逆方向に伝播させ、各層における結合の強さを調整していきます。この誤差を減らす方向に結合の強さを調整することで、ネットワークは徐々に正解データに近い出力を得られるようになり、学習が進んでいきます。

この誤差逆伝播法は、特に多層パーセプトロンと呼ばれる種類のニューラルネットワークにおいて、効率的な学習を可能にします。多層パーセプトロンは、入力層、隠れ層、出力層という複数の層から構成されており、各層には多数のノード（ニューロン）が存在し、それらのノードが結合の強さで結びついています。層が深くなるほど、ネットワークは複雑なパターンを学習できるようになりますが、同時に学習の難しさも増大します。誤差逆伝播法はこのような複雑なネットワークの学習を効率的に行うことを可能にするため、深層学習と呼ばれる分野の発展に大きく貢献しました。

誤差逆伝播法の利点は、その計算過程が直感的に理解しやすい点にあります。誤差を出力側から入力側へ逆方向に伝播させるという考え方は、人間の学習過程にも類似している部分があり、その仕組みを理解しやすいという利点があります。また、誤差を効率的に計算できるため、大規模なデータセットを用いた学習にも適用可能です。

誤差逆伝播法は現在の人工知能技術の根幹を支える重要な技術であり、今後ますます発展していく人工知能分野においても中心的な役割を果たし続けると考えられます。画像認識、音声認識、自然言語処理など、様々な分野で応用されており、今後も更なる発展と応用が期待されます。