データの関係を読み解く:相関とは

AIを知りたい
先生、「相関」って言葉がよくわからないんですけど、簡単に説明してもらえますか?

AIエンジニア
そうだな。たとえば、アイスクリームの売り上げと気温を考えてみよう。気温が上がるとアイスクリームの売り上げも増えるよね。こういう関係を「相関」と言うんだ。2つのものがどれくらい似通った変化をするかを表すんだよ。

AIを知りたい
なるほど。でも、アイスクリームがよく売れるから気温が上がる、とは言えないですよね?

AIエンジニア
その通り!まさにそこがポイントだ。アイスクリームと気温は「相関」しているけど、アイスクリームが気温を上げる「原因」になっているわけではない。AIもデータから「相関」を見つけるのは得意だけど、それが「原因」なのかどうかまではわからないんだ。そこを見極めるのは人間の役割なんだよ。
相関とは。
人工知能でよく使われる「相関」という言葉について説明します。「相関」とは、二つ以上のものがあるとき、それらがどれくらい似ているかを示す「類似度」のことです。例えば、アイスクリームの売り上げと気温の関係のように、片方が増えるともう片方も増える関係を「正の相関関係」と言います。逆に、日傘の売り上げと気温の関係のように、片方が増えるともう片方が減る関係を「負の相関関係」と言います。そして、この「類似度」の強さをマイナス1から1までの数字で表したものを「相関係数」と言います。機械学習で見つかるのは、物事の「相関」だけで、原因と結果のつながり、つまり「因果」ではありません。相関関係があるからといって、本当に関係しているとは限らないのです。例えば、アイスクリームの売り上げと気温に相関関係があっても、アイスクリームの売り上げが上がったから気温が上がったとは言えませんよね。複数の事柄に関係があることは分かっても、本当につながりがあるのか、なぜそうなるのかを明らかにするのは人間の役割です。
相関の基礎

ものごとの関係性を数値で表すことを、相関と言います。2つの数値の間にある関係の強さを示す統計的な尺度であり、-1から1までの数値で表されます。この数値を相関係数と呼びます。相関係数が1に近いほど正の相関が強く、-1に近いほど負の相関が強いことを示します。0に近い場合は、2つの数値の間に関係がない、つまり無相関であることを意味します。
例えば、夏の暑い時期にアイスクリームの売り上げが伸びる現象を考えてみましょう。気温が高い日にはアイスクリームがよく売れ、気温が低い日にはあまり売れません。これは気温とアイスクリームの売り上げに正の相関があることを示す典型的な例です。気温が上がれば上がるほど、アイスクリームの売り上げも増える傾向にあるため、相関係数は1に近づきます。
反対に、気温と厚着の関係を考えてみましょう。気温が低い冬には、多くの人が厚着をしますが、気温が高くなるにつれて、厚着をする人は減っていきます。これは気温と厚着の枚数の間に負の相関があることを意味します。気温が上がれば上がるほど厚着の枚数は減る傾向にあるため、相関係数は-1に近づきます。
相関関係は、2つの数値の間に因果関係があることを必ずしも意味するものではないことに注意が必要です。例えば、アイスクリームの売り上げと水難事故の発生件数には正の相関が見られるかもしれません。これは、気温が高い日にアイスクリームの売り上げも水難事故の発生件数も増えるためです。しかし、アイスクリームをたくさん食べたから水難事故に遭うわけではありません。このように、見かけ上の相関関係に惑わされず、背後にある要因を注意深く考察することが重要です。相関を理解することで、ものごとの関係性を客観的に捉え、より深い洞察を得ることができるようになります。
| 相関係数 | 相関の強さ | 例 | 説明 |
|---|---|---|---|
| 1に近い | 強い正の相関 | 気温とアイスクリームの売り上げ | 気温が高いほど、アイスクリームの売り上げも増える |
| -1に近い | 強い負の相関 | 気温と厚着 | 気温が低いほど、厚着をする人が増える |
| 0に近い | 無相関 | アイスクリームの売り上げと水難事故発生件数(擬似相関) | 因果関係がない例。共通の要因(気温)によって相関があるように見える |
相関係数の役割

物事の関係性を数値で表す方法のひとつに、相関係数があります。これは、二つのものがどれだけ関係しているかを客観的に示す便利な道具です。相関係数は、必ず-1から1までの間の値になります。この数字を見るだけで、関係性の強さや種類をすぐに理解することができます。
もし相関係数が1に近い値を示していたら、二つのものは「正の相関」があると言います。これは、片方が増えるともう片方も増える関係です。例えば、気温が上がるとアイスクリームの売り上げも伸びるといった関係が考えられます。もし相関係数が0.8だったとすれば、気温とアイスクリームの売り上げには強い正の相関があると言えるでしょう。
逆に、相関係数が-1に近い値を示す場合は、「負の相関」があると言います。これは、片方が増えるともう片方が減る関係です。例えば、気温が下がると厚着をする枚数が増えるといった関係です。もし相関係数が-0.7だったとすれば、気温と厚着の枚数には強い負の相関があると言えるでしょう。
最後に、相関係数が0に近い場合は、二つのものの間に「相関が弱い」、もしくは「相関がない」と判断できます。例えば、サイコロを振った時の目と、明日の気温には、特別な関係性はないと考えられます。このような場合、相関係数は0に近くなるはずです。
このように、相関係数を使うことで、様々な事柄の関係性をより深く理解することができます。数値で表すことで、曖昧な印象ではなく、はっきりとした形で関係性の強さを捉えることができるのです。
| 相関係数 | 相関の種類 | 関係性 | 例 |
|---|---|---|---|
| 1に近い値 (例: 0.8) | 正の相関 | 片方が増えるともう片方も増える | 気温の上昇とアイスクリームの売り上げ増加 |
| -1に近い値 (例: -0.7) | 負の相関 | 片方が増えるともう片方が減る | 気温の低下と厚着の枚数増加 |
| 0に近い値 | 相関が弱い、または相関がない | 二つのものに特別な関係性はない | サイコロの目と明日の気温 |
正の相関と負の相関

ものごとの関係性を数値で表す方法として、相関という考え方があります。相関には大きく分けて、正の相関と負の相関の二つの種類があります。
正の相関とは、一方の値が増加すると、もう一方の値も増加する関係のことです。例えば、学習に費やす時間と試験の得点の関係を考えてみましょう。一般的に、学習時間が長ければ長いほど、試験の得点は高くなる傾向があります。このように、一方が増えればもう一方も増える関係が、正の相関です。他にも、商品の販売数と売上金額の関係も正の相関と言えるでしょう。販売数が増えれば、売上金額も増えるのが自然な流れです。また、植物の成長と日照時間の長さ、気温とアイスクリームの売上なども正の相関の例として挙げられます。日照時間が長くなるほど植物はよく育ち、気温が高いほどアイスクリームがよく売れるといった具合です。
一方、負の相関とは、一方の値が増加すると、もう一方の値は減少する関係のことです。例えば、運動時間と体重の関係を考えてみましょう。運動時間を長く取れば取るほど、体重は減少する傾向があります。このように、一方が増えればもう一方が減る関係が、負の相関です。他にも、製品の価格と需要の関係も負の相関の例として挙げられます。価格が高くなればなるほど、需要は少なくなるのが一般的です。また、残業時間と睡眠時間、ある商品の値下げ率とその商品の売上高なども負の相関と言えるでしょう。残業時間が増えれば睡眠時間は減少し、値下げ率が大きくなれば売上高は減少するといった具合です。
このように、相関には正と負の二つの種類があり、ものごとの関係性によって正の相関と負の相関を使い分けることで、ものごとの関係性をより深く理解することができます。
| 相関の種類 | 説明 | 例 |
|---|---|---|
| 正の相関 | 一方の値が増加すると、もう一方の値も増加する関係 |
|
| 負の相関 | 一方の値が増加すると、もう一方の値は減少する関係 |
|
相関と因果の違い

「相関」と「因果」は、言葉の響きが似ていることもあり混同されがちですが、実際には全く異なる概念です。データ分析を行う際、この違いを理解することは非常に重要です。
まず「相関」とは、二つの事柄に見られる関係性を指します。例えば、アイスクリームの売り上げと気温には正の相関があります。気温が上がればアイスクリームの売り上げも伸び、気温が下がれば売り上げも落ちるといった具合です。また、反対に負の相関関係もあります。例えば、厚着をする人の数と気温には負の相関があります。気温が低いほど厚着をする人が増え、気温が高いほど厚着をする人は減るからです。このように、相関関係とは二つの事柄が共に変化する傾向を示すものであり、一方が他方の原因となっていることを意味するわけではありません。
一方、「因果」とは、一方の事柄が他方の事柄の直接的な原因となっている関係を指します。例えば、熱いコーヒーを飲むと体が温まる、といった関係です。熱いコーヒーを飲むという行動が、体が温まるという結果を生み出しているため、これは因果関係と言えます。
相関関係と因果関係の違いを理解するために、先ほどのアイスクリームの売り上げの例をもう一度考えてみましょう。アイスクリームの売り上げと水難事故の発生件数には正の相関が見られることがあります。気温が高い時期にはアイスクリームの売り上げも伸び、水遊びをする人も増えるため、水難事故も増えるためです。しかし、これはアイスクリームを食べることで水難事故が起こるという因果関係を示しているわけではありません。真の原因は「気温」という第三の要素にあります。気温の上昇が、アイスクリームの売り上げ増加と水難事故の増加、両方の原因となっているのです。このように、相関関係があるからといって因果関係があると判断するのは早計です。隠れた要因がないか、よく吟味する必要があります。
| 項目 | 説明 | 例 |
|---|---|---|
| 相関 | 二つの事柄に見られる関係性。一方が他方の原因となっていることを意味するわけではない。 |
|
| 因果 | 一方の事柄が他方の事柄の直接的な原因となっている関係。 | 熱いコーヒーを飲むと体が温まる |
機械学習における相関

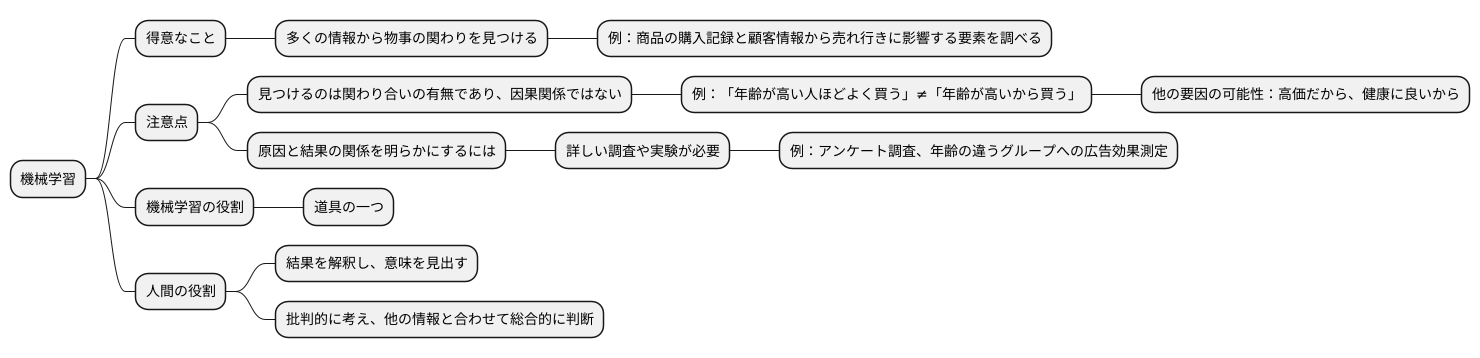
機械学習は、多くの情報から物事の関わりを見つけるのが得意です。まるで探偵のように、膨大なデータの中から手がかりを探し出し、隠れた繋がりを明らかにします。例えば、ある商品の購入記録と顧客の年齢、性別、住んでいる場所などの情報があれば、機械学習を使って商品の売れ行きに影響を与える要素を調べることができます。
しかし、機械学習が見つけるのは、物事の関わり合いの有無であり、原因と結果の関係ではありません。例えば、「年齢が高い人ほどこの商品をよく買う」という繋がりが見つかったとしても、それは「年齢が高いからこの商品を買う」という因果関係を示しているとは限りません。もしかしたら、その商品は高価で、年齢が高い人ほどお金を持っているから買う人が多いのかもしれませんし、あるいは、その商品は健康に良いとされ、年齢が高い人ほど健康に気を遣うから買う人が多いのかもしれません。このように、物事の関わり合いと原因と結果の関係は別物です。
原因と結果の関係を明らかにするには、もっと詳しい調査や実験が必要です。例えば、年齢が高い人にアンケート調査を行い、なぜその商品を買ったのか理由を尋ねたり、年齢の違う二つのグループに同じ広告を見せて、商品の購入率に違いがあるかを調べたりする必要があります。機械学習は、あくまでも道具の一つに過ぎません。その結果をどう解釈し、どんな意味を見出すかは、私たち人間の役割です。機械学習の結果を鵜呑みにせず、批判的に考え、他の情報と合わせて総合的に判断することが大切です。そうすることで、初めてデータの奥に隠された真実を明らかにし、より良い意思決定を行うことができるのです。
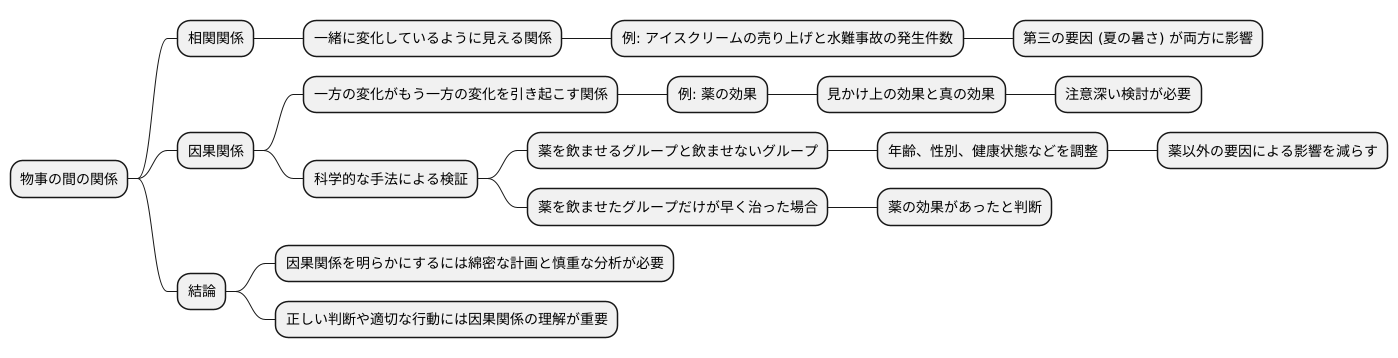
因果関係の考察

物事の間の関係には、一緒に変化しているように見える関係と、一方の変化がもう一方の変化を引き起こしている関係の二種類があります。前者を相関関係、後者を因果関係と言います。
例えば、アイスクリームの売り上げと水難事故の発生件数には相関関係が見られます。どちらも夏の暑い時期に増加するからです。しかし、アイスクリームをたくさん食べたからといって、水難事故に遭うわけではありません。これは、第三の要因、つまり夏の暑さというものが、両方に影響を与えているためです。
もし新しい薬の効果を確かめたいとしましょう。薬を飲んだ人と飲んでいない人を比べて、飲んだ人の方が病気が治りやすいという結果が出たとします。これは一見、薬に効果があるように思えます。しかし、本当に薬のおかげで病気が治ったと言えるでしょうか?もしかしたら、薬を飲んだ人はたまたま病気が治りやすい体質の人が多かったのかもしれません。あるいは、薬を飲んだことで安心感が生まれ、それが病状の改善につながったのかもしれません。このように、見かけ上の効果を真の効果と区別するためには、注意深い検討が必要です。
そこで、科学的な手法を用いて因果関係を検証します。薬の効果を検証する場合、薬を飲ませるグループと飲ませないグループを作ります。この時、両方のグループの年齢や性別、もともとの健康状態などがなるべく同じになるように調整します。こうすることで、薬以外の要因による影響を減らすことができます。そして、薬を飲ませたグループだけが病気が早く治った場合、初めて薬の効果があったと判断できます。
このように、因果関係を明らかにするには、綿密な計画と慎重な分析が必要です。因果関係を特定するのは簡単なことではありませんが、正しい判断や適切な行動をするためには、因果関係を理解することが非常に重要です。