標準偏差:データのばらつきを理解する

AIを知りたい
先生、「標準偏差」ってどういう意味ですか? AIの勉強でよく出てくるんですが、難しくて…

AIエンジニア
なるほど。標準偏差は、データが平均値からどれくらいばらついているかを表す値だよ。例えば、クラス全員のテストの点数を考えてみよう。

AIを知りたい
はい。平均点が高いほど良いってことですよね?

AIエンジニア
そうだけど、平均点だけでは全体像は分からない。標準偏差が小さいと、みんな平均点に近い点数を取っている。つまり、実力の差が小さいことを示しているんだ。逆に標準偏差が大きいと、高い点の人もいれば低い点の人もいる、つまり実力の差が大きいことを示すんだよ。
標準偏差とは。
データのばらつき具合を示す指標である「標準偏差」について説明します。これは、数学、統計学、機械学習といった分野でよく使われる用語です。
標準偏差とは

標準偏差とは、数値データのばらつき具合、つまり、データがどれくらい散らばっているかを示す指標です。平均値だけではわからないデータの性質を捉えるために使われます。たとえば、学校のテストで考えてみましょう。同じクラスで平均点が70点だったとしても、全員がちょうど70点だった場合と、30点から100点まで点数がバラバラだった場合では、様子が全く違いますよね。標準偏差は、このような違いを数値で表すことができます。
標準偏差を計算するには、まず平均値を求めます。それから、それぞれのデータが平均値からどれくらい離れているか(これを偏差といいます)を計算します。偏差をそのまま平均してしまうと、プラスとマイナスで打ち消しあってゼロになってしまうため、偏差を二乗してから平均します。こうして出てきた値を分散といいます。分散は偏差の二乗の平均なので、元のデータよりも単位が大きくなってしまっています。そこで、分散の平方根をとることで、元のデータと同じ単位に戻します。これが標準偏差です。標準偏差が大きいほど、データは平均値から遠く離れて散らばっていることを意味します。
標準偏差は、統計学や機械学習など、様々な分野で活用されています。たとえば、製造業では、製品の品質管理に標準偏差が使われています。製品の寸法や重さのばらつきを標準偏差で管理することで、不良品の発生を抑えることができます。また、金融の世界でも、投資のリスクを測る指標として標準偏差が使われています。標準偏差が大きいほど、投資のリターンも大きく変動する可能性が高いことを示しています。このように、標準偏差はデータのばらつきを理解し、分析するための重要な道具となっています。
| 用語 | 説明 | 例 |
|---|---|---|
| 標準偏差 | データのばらつき具合を示す指標。平均値からどれくらいデータが離れているかを表す。 | テストの点数、製品の寸法、投資のリターン |
| 平均値 | データの合計をデータの数で割った値。 | テストの平均点 |
| 偏差 | それぞれのデータが平均値からどれくらい離れているかの値。 | 個々のテストの点数と平均点の差 |
| 分散 | 偏差の二乗の平均。 | 偏差の二乗を合計し、データの数で割った値 |
| 標準偏差の用途 | 品質管理、リスク管理など | 製品の寸法のばらつきを抑える、投資のリスクを測る |
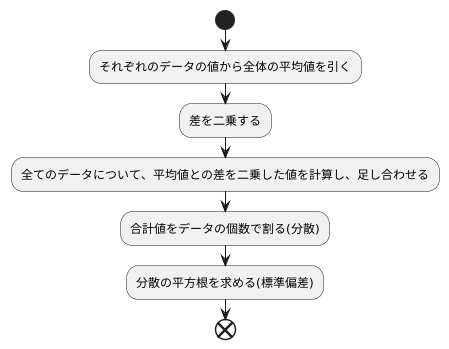
計算方法

計算方法は、少し込み入ったように見えるかもしれませんが、順を追って説明します。まず、それぞれのデータの値から全体の平均値を引きます。これは、個々のデータが平均からどれくらい離れているかを示すものです。次に、この差を二乗します。二乗する理由は、平均値からのずれの大きさを正負に関わらず測るためです。もし二乗しなければ、プラスのずれとマイナスのずれが打ち消し合ってしまい、全体のばらつきが正しく表せません。すべてのデータについて、平均値との差を二乗した値を計算したら、それらを全て足し合わせます。これで、データ全体のばらつきの大きさを一つの数値で表すことができます。さらに、この合計値をデータの個数で割ります。データの個数で割ることで、データの数が異なってもばらつきの大きさを比較できるように調整します。この計算で得られた値は「分散」と呼ばれ、データのばらつきの程度を示す指標となります。最後に、分散の平方根を求めます。平方根を計算することで、元のデータと同じ単位でばらつきを表現できます。この平方根が「標準偏差」です。数式を理解すると、標準偏差がどのようにデータのばらつき具合を捉えているのかを深く理解できるはずです。今では、計算表を作るための道具や統計を扱う道具を使えば簡単に計算できますので、実際に自分の手で計算してみるのも良いでしょう。これらの道具を使うことで、複雑な計算も容易に行うことができます。計算の過程をよく理解することで、データの特性をより深く理解し、分析に役立てることができます。
活用例

標準偏差は、数値データのばらつき具合を測る指標であり、様々な分野で活用されています。 例えば、金融業界を考えてみましょう。日々変動する株価の動きを理解し、投資判断を行う際に、標準偏差は重要な役割を果たします。株価の上がり下がりの激しさを標準偏差という数値で表すことで、投資に伴う危険の度合いを推し量ることができます。標準偏差が大きい場合、株価の変動も大きい、つまり価格が大きく上下する可能性が高いことを示しており、危険な投資と判断できます。逆に標準偏差が小さい場合は、株価の変動も比較的小さく、安定した投資先と判断できます。このように、標準偏差は投資における安全性を評価する重要な判断材料となります。
製造業においても、標準偏差は製品の品質管理に欠かせないツールです。例えば、ネジの直径を製造過程で測定すると、必ずしも設計図通りの寸法にはなりません。どうしてもわずかな誤差が生じ、ばらつきが発生します。このばらつきを標準偏差で数値化し、管理することで、不良品の発生を未然に防ぐことができます。標準偏差が大きければ、製品のばらつきも大きいことを意味し、不良品が発生する可能性が高くなります。製造過程を改善し、標準偏差を小さくすることで、製品の品質を安定させることができます。
医療分野でも標準偏差は活用されています。健康診断などで得られる検査データ、例えば血液検査の数値などは、ある程度の範囲内でばらつきがあるのが普通です。このばらつきを標準偏差で表すことで、検査データの異常値を検出することができます。もし、ある人の検査値の標準偏差が極端に大きい場合、何らかの病気が隠れている可能性があり、精密検査が必要となるかもしれません。
学術研究においても、実験データの解析に標準偏差は必須です。実験では同じ条件下で何度も測定を行いますが、得られる結果は必ずしも一致しません。この実験結果のばらつきを標準偏差で数値化することで、実験の精度を評価したり、異なる実験結果を比較したりすることができます。
このように、標準偏差は様々な分野で活用され、データに基づいた意思決定を支援する重要な役割を担っています。標準偏差は、データのばらつきという漠然とした概念を具体的な数値で捉えることで、物事をより客観的に判断することを可能にするのです。
| 分野 | 標準偏差の活用 | 標準偏差が大きい場合 | 標準偏差が小さい場合 |
|---|---|---|---|
| 金融 | 投資リスクの評価 | 株価変動が大きく、危険な投資 | 株価変動が小さく、安定した投資 |
| 製造業 | 製品の品質管理 | 製品のばらつきが大きく、不良品発生の可能性が高い | 製品のばらつきが小さく、品質が安定 |
| 医療 | 検査データの異常値検出 | 病気が隠れている可能性 | (特記なし) |
| 学術研究 | 実験データの解析、精度の評価、結果の比較 | 実験の精度が低い可能性 | 実験の精度が高い可能性 |
分散との関係

データのばらつき具合を知ることは、統計分析において非常に大切です。そのばらつき具合を表す尺度として、標準偏差と分散があります。これらは密接に関連しており、どちらを用いるかによって、データの解釈の仕方が変わってきます。
標準偏差は、データが平均値からどれくらい離れているかを表す数値です。標準偏差の値が大きいほど、データは平均値から遠く、ばらつきが大きいことを示します。また、標準偏差は元のデータと同じ単位を持つため、計算結果を直感的に理解しやすいという利点があります。例えば、ある商品の価格の平均値が1000円で、標準偏差が100円であれば、多くの商品の価格は900円から1100円の間にあると推測できます。
一方、分散は標準偏差を二乗した値です。つまり、標準偏差を求める計算過程においては、まず分散を求め、その後に分散の平方根を計算することで標準偏差を算出します。分散もデータのばらつき具合を示す指標ですが、標準偏差と異なり、元のデータと単位が異なってしまいます。このため、分散の値を直接解釈することは難しく、標準偏差と比較して直感的に理解しづらいという欠点があります。例えば、先ほどの商品の価格の例で考えると、分散は10000円${^2}$となりますが、この値から直接商品の価格のばらつき具合をイメージすることは難しいでしょう。
このように、分散と標準偏差はどちらもデータのばらつきを表す指標ですが、それぞれに特性があります。標準偏差は解釈のしやすさ、分散は計算過程における重要性という点でそれぞれ利点を持っています。そのため、データ分析の目的や状況に応じて、どちらの指標を用いるかを適切に選択することが重要です。具体的には、データのばらつき具合を直感的に理解したい場合は標準偏差を、より複雑な統計計算を行う場合は分散を用いると良いでしょう。
| 尺度 | 説明 | 利点 | 欠点 | 使用例 |
|---|---|---|---|---|
| 標準偏差 | データが平均値からどれくらい離れているかを表す数値。元のデータと同じ単位を持つ。 | 計算結果を直感的に理解しやすい。 | – | データのばらつき具合を直感的に理解したい場合。 |
| 分散 | 標準偏差を二乗した値。元のデータと単位が異なる。 | 計算過程における重要性。 | 値を直接解釈することは難しく、直感的に理解しづらい。 | より複雑な統計計算を行う場合。 |
正規分布における役割

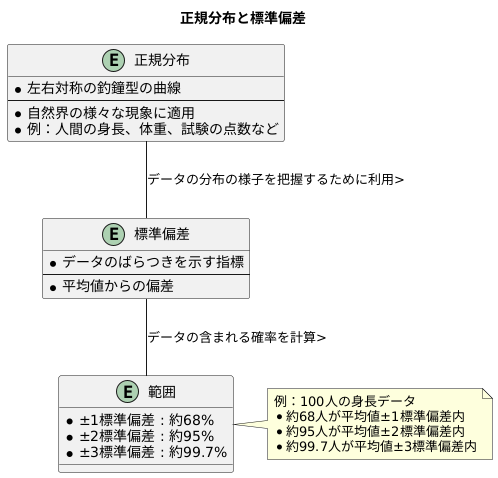
左右対称の釣鐘型の曲線で表される正規分布は、確率や統計の世界で欠かせない存在です。自然界の様々な現象、例えば人間の身長や体重、試験の点数など、多くのデータがこの正規分布に従うことが知られています。この分布の特徴を理解する上で、標準偏差は極めて重要な役割を担っています。
標準偏差とは、データが平均値からどのくらいばらついているかを示す指標です。正規分布においては、この標準偏差を用いることで、データの分布の様子をより詳しく把握できます。具体的には、平均値と標準偏差を組み合わせることで、ある範囲にデータがどのくらいの確率で含まれるかを計算できます。平均値を中心として、平均値プラス標準偏差、平均値マイナス標準偏差の範囲には、全体の約68%のデータが含まれます。つまり、100人の身長のデータがあるとすれば、約68人の身長がこの範囲に収まるということです。
さらに、平均値プラス2倍の標準偏差、平均値マイナス2倍の標準偏差の範囲には、全体の約95%のデータが含まれます。この範囲には、先ほどの100人の身長データのうち、約95人の身長が含まれる計算になります。そして、平均値プラス3倍の標準偏差、平均値マイナス3倍の標準偏差の範囲になると、全体の約99.7%ものデータが含まれます。このように、標準偏差を用いることで、データの大部分がどの範囲に収まっているかを把握できます。
正規分布と標準偏差の理解は、統計学や機械学習といった分野では必須の知識です。なぜなら、多くの分析手法が、データが正規分布に従うことを前提としているからです。標準偏差を理解することで、データの特性を深く理解し、様々な分析手法を正しく適用できるようになります。これにより、より正確な予測や分析結果を得ることが可能になります。
より深く理解するために

データのばらつき具合を知ることは、全体像を掴む上で欠かせません。平均値だけではデータの全体像を把握するには不十分です。例えば、二つの集団の平均点が同じだったとしても、それぞれの集団内で点数がどのようにばらついているかは大きく異なる可能性があります。データのばらつき具合を数値化したものの一つが標準偏差です。標準偏差は、データが平均値からどれくらい離れているかを平均的に示す指標です。
標準偏差を計算するには、まず各データと平均値との差を求めます。この差を偏差と呼びます。偏差を二乗し、その合計をデータの個数で割った値の平方根が標準偏差です。二乗する理由は、偏差には正負の値が含まれており、そのまま合計すると相殺されてしまうからです。二乗することで、偏差の大きさを正の値で捉えることができます。標準偏差が小さい場合は、データが平均値付近に集まっていることを示し、大きい場合はデータが平均値から大きく散らばっていることを示します。
標準偏差を理解することで、データのばらつきを客観的に評価し、より深い分析が可能になります。例えば、製造業では製品の品質管理に標準偏差が用いられます。製品の寸法や重量のばらつきを標準偏差で管理することで、不良品の発生率を減らすことができます。金融業界では、投資のリスク管理に標準偏差が使われます。投資商品の価格変動のばらつきを標準偏差で表すことで、リスクの大きさを評価することができます。
標準偏差についてより深く学ぶには、統計学の教科書を読む、インターネット上の学習サイトを利用する、統計ソフトを用いて実際にデータを分析してみるなどの方法があります。数式だけでなく、具体的な事例を通して学ぶことで、より実践的な理解に繋がるでしょう。標準偏差を理解することは、データ分析能力の向上に大きく貢献します。日々の生活の中でも、データに触れる機会は多くあります。標準偏差を理解することで、データをより深く理解し、より良い判断を行うことができるようになるでしょう。
| 項目 | 説明 |
|---|---|
| 標準偏差の目的 | データのばらつき具合を数値化し、全体像を把握するため。平均値だけでは不十分なデータの分布状態を理解する。 |
| 標準偏差の計算方法 | 1. 各データと平均値の差(偏差)を求める。 2. 偏差を二乗する。 3. 二乗した偏差の合計をデータの個数で割る。 4. 3. の平方根を求める。 |
| 標準偏差の意味 | データが平均値からどれくらい離れているかを平均的に示す指標。小さい値はデータが平均値付近に集中、大きい値はデータが散らばっていることを示す。 |
| 標準偏差の活用例 |
|
| 標準偏差の学習方法 |
|
