シンプソンのパラドックス:隠れた真実

AIを知りたい
先生、「シンプソンのパラドックス」ってどういう意味ですか?説明文を読んでも、よく分からなくて…

AIエンジニア
なるほど。簡単に言うと、全体で見るとある傾向があるのに、それをいくつかのグループに分けて見てみると、それぞれのグループでは全く逆の傾向が見られる、という現象のことだよ。

AIを知りたい
えーっと、全体では右肩上がりなのに、グループごとに見てみると右肩下がり…みたいなことですか?

AIエンジニア
そうそう、そういうこと。まるで全体と部分が食い違っているように見える、不思議な現象なんだ。もう少し具体的な例で考えてみようか。
シンプソンのパラドックスとは。
人工知能に関係する言葉である「シンプソンの逆説」について説明します。ただ、言葉だけでは分かりにくいと思いますので、次の節で具体的な例を使って改めて説明します。
全体像と部分像のずれ

物事全体を見たときと、それを細かく分けて見たときで、全く逆の傾向が見えてしまうことがあります。これをシンプソンの逆説と呼びます。全体で見るとある傾向が正しいように見えても、実は個々の集団で見ると全く逆の結論になるという、統計の落とし穴の一つです。
例えば、新しい薬の効果を調べるとしましょう。薬Aと薬Bを患者全体で比較すると、薬Aの方がよく効くように見えるとします。しかし、患者の年齢で分けて考えてみると、若い人にも高齢者にも、薬Bの方が効果が高いという結果になるかもしれません。全体で見ると薬Aが優勢に見えたにもかかわらず、年齢という集団に分けてみると、薬Bの方が効果的だったという逆転現象が起こるのです。
これは、年齢層によって患者数が大きく異なる場合などに起こりえます。高齢者の患者数が非常に多く、たまたま薬Aを飲んだ高齢者の回復率が低いと、全体の結果に大きな影響を与えてしまうのです。つまり、見かけ上は薬Aが効果的に見えても、実際は年齢層ごとに適切な薬を選択する必要があるということを示しています。
この例のように、全体像だけを見て判断すると、誤った結論に至る危険性があります。物事の真実を見抜くためには、全体像だけでなく、様々な切り口でデータを分析し、隠された真実を明らかにする必要があります。データ分析を行う際には、多角的な視点を持つことが大切です。一つの側面だけでなく、様々な角度から物事を見ることで、より正確な判断ができるようになります。
具体的な例で理解を深める

野球を題材に、シンプソンの逆説について詳しく見ていきましょう。この逆説は、一見すると矛盾しているように見えるデータの傾向を示すものです。全体で見るとある結論が導かれるのに、それをいくつかのグループに分けてみると、全く逆の結論が出てしまう、という不思議な現象です。
例として、佐藤選手と田中選手、二人の野球選手を比べてみます。佐藤選手はシーズン全体の打率で田中選手を上回っていました。一見すると、佐藤選手の方が優れているように思えます。ところが、シーズンを前半と後半に分け、それぞれの期間での打率を計算してみると、前半も後半も、田中選手の方が佐藤選手よりも高い打率を残していたのです。これがシンプソンの逆説です。全体では佐藤選手が優勢なのに、細かく見ていくと田中選手の方が常に上回っているという、一見矛盾した結果が出てしまうのです。
では、なぜこのようなことが起こるのでしょうか?具体的な数字で考えてみましょう。仮に、佐藤選手が前半に10回打席に立って2安打、後半に100回打席に立って20安打だったとします。全体の打率は22割100分の22です。一方、田中選手は前半に100回打席に立って30安打、後半に10回打席に立って3安打だったとしましょう。田中選手の全体の打率は33割100分の33です。このように、打席数の違いが結果に大きく影響を与えていることが分かります。田中選手は前半に多くの打席に立ち好成績を残しましたが、後半は打席数が少なかった。佐藤選手はその逆で、後半に多くの打席に立ちました。全体で見ると、後半に多く打席に立った佐藤選手の方が打率が高く見えますが、実際には、それぞれの期間で比較すると田中選手の方が高い打率を維持していたのです。
この例が示すように、データを見る時は単純な比較だけでなく、背後にある状況を理解することが大切です。データがどのように集計され、グループ分けされているのかを注意深く確認しなければ、誤った結論を導きかねません。様々な角度からデータを確認し、隠れた要因がないかを探ることで、より正確な判断ができるようになります。
| 選手名 | 打率 | ||
|---|---|---|---|
| 前半 | 後半 | 全体 | |
| 佐藤選手 | 2/10 = .200 | 20/100 = .200 | 22/110 = .200 |
| 田中選手 | 30/100 = .300 | 3/10 = .300 | 33/110 = .300 |
一見、全体の結果では佐藤選手が田中選手を上回っているように見えますが、前半と後半の成績を個別に見てみると、田中選手が常に佐藤選手を上回っています。これは、各期間の打席数に大きな差があるために起こる現象で、シンプソンの逆説と呼ばれます。
誤った解釈を防ぐには

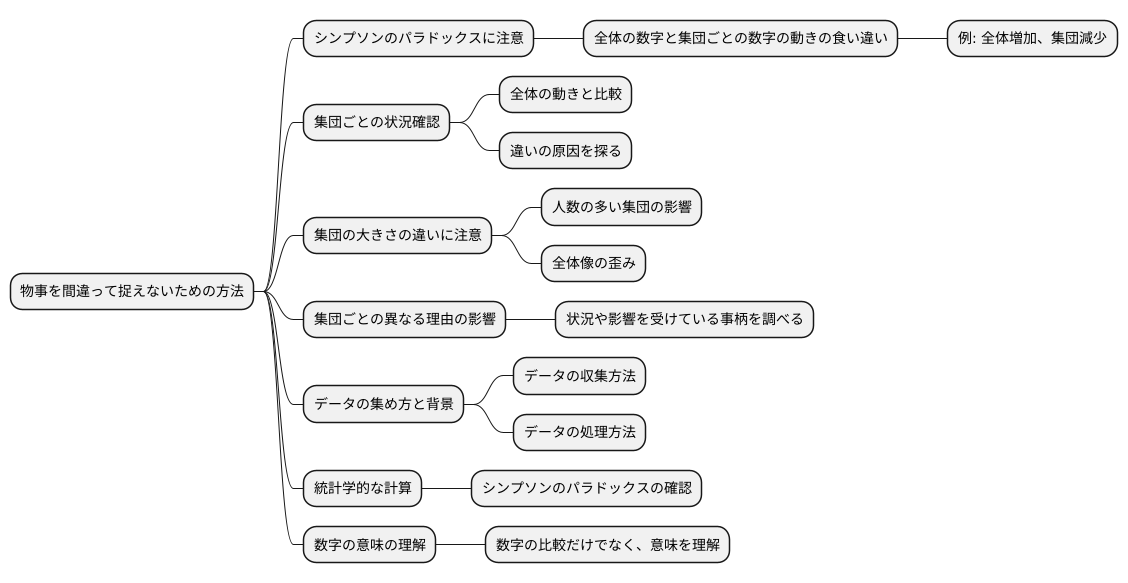
物事を間違って捉えてしまうことを防ぐには、様々な方法があります。特に、全体的な数字の動きと、集団ごとの数字の動きが食い違う現象(シンプソンのパラドックスと呼ばれるもの)には注意が必要です。
まず、全体像だけでなく、それぞれの集団がどのような状況なのかを必ず確認しましょう。全体で見ると増加しているように見えても、集団ごとに見てみると減少している場合もあります。全体と集団ごとの動きの違いに気づいたら、なぜそのような違いが生じているのか、その原因を丁寧に探ることが大切です。
例えば、集団の大きさが大きく異なっている場合に、このような現象が起こりやすいです。人数の多い集団と少ない集団を一緒に見てしまうと、人数の多い集団の動きに引っ張られて、全体像が歪んで見えてしまうことがあります。また、集団ごとに異なる理由が影響している場合も、全体像を正しく捉えるのが難しくなります。それぞれの集団が置かれている状況や、影響を受けている事柄を詳しく調べることで、より正確な判断ができます。
データが集められた方法や、その背景にある状況にも目を向ける必要があります。データはどのように集められ、どのように処理されたのか。こうした情報を知ることで、数字の本当の意味が見えてきます。
加えて、統計学的な計算方法を使って、この現象が起こっているかどうかを確かめるのも良いでしょう。こうした様々な方法を組み合わせることで、数字の奥に隠された真実を見抜き、より適切な判断を下せるようになります。データを見る際には、ただ数字を比べるだけでなく、数字が持つ意味を深く理解することが重要です。
起こりうる場面とその影響

起こりうる場面とその影響について、より詳しく見ていきましょう。
医療の分野では、新しい薬の効果を確かめる際に、患者さんの年齢や性別といった大切な点を無視して、全体の結果だけで判断すると、間違った結論に達してしまうことがあります。例えば、ある新薬が全体で見ると効果があるように見えても、若い患者さんには効果的で、高齢の患者さんには効果がないといった隠れた事実を見逃してしまうかもしれません。これは、年齢層によって薬の効き方が違うにも関わらず、全体でまとめて見てしまうことで、その違いが見えなくなってしまうからです。
教育の分野でも同様のことが言えます。異なる学校の生徒たちの成績を単純に比較すると、それぞれの学校の特徴や教育の環境の違いを無視することになり、公平な評価ができなくなります。ある学校は学習に力を入れているため平均点が高く、別の学校はスポーツに力を入れているため平均点が低いといった場合、単純に平均点だけで比較すると、学習に力を入れている学校の方が優れているという誤った判断をしてしまう可能性があります。
会社の経営においても、顧客層や地域ごとの売上情報をきちんと分析しなければ、効果的な販売戦略を立てることはできません。例えば、ある商品が全体で見ると売上が伸びているように見えても、特定の地域では売上が落ち込んでいるといった状況を見逃してしまうかもしれません。地域ごとの顧客の好みや経済状況などを考慮せずに、全体だけで判断すると、効果的な販売戦略を立てられないばかりか、売上の減少につながる可能性もあります。
このように、様々な分野で物事を判断する際に、全体像だけを見て、個々の集団の違いを無視してしまうと、誤った結論に達する危険性があります。データ分析を行う際には、このような落とし穴に注意し、データの背後にある様々な要因を丁寧に見ていく必要があります。多角的な視点から物事を捉え、様々な角度から情報を分析することで、より正確で効果的な判断ができるようになります。
| 分野 | 起こりうる場面 | 影響 | 例 |
|---|---|---|---|
| 医療 | 新薬の効果検証で患者属性を無視 | 年齢層別での効果差を見逃し、誤った結論に至る | 新薬が全体では効果あるように見えても、高齢者には効果がない可能性を見逃す |
| 教育 | 異なる学校の生徒の成績を単純比較 | 学校の特徴や教育環境の違いを無視した不公平な評価 | 学習重視の学校とスポーツ重視の学校を平均点だけで比較し、誤った判断をする |
| 会社経営 | 顧客層や地域ごとの売上情報を分析せず | 効果的な販売戦略を立てられない、売上減少の可能性 | 商品全体の売上は伸びていても、特定地域で落ち込んでいる状況を見逃す |
データ分析の重要性

情報の集まりを詳しく調べ、物事の現状やこれから起こりうる事柄を明らかにする事は、今の時代とても大切です。その大切さを示す良い例として、「シンプソンの逆説」というものがあります。これは、一見すると正しいように見える結論が、隠れた要因によって全く違うものになってしまうという現象です。
情報の分析は、ただ数字を並べるだけでは意味がありません。数字の背景にある状況をしっかりと理解し、様々な角度から数字を検証する必要があります。例えば、情報の集め方、情報の分け方、そして情報に影響を与える可能性のある様々な要因を考えなければ、正しい結論を導き出す事はできません。
例えば、ある病気の治療法を比較するとします。全体で見ると、治療法Aの方が効果が高いように見えます。しかし、患者の年齢層で分けてみると、若い患者には治療法B、高齢の患者には治療法Aの方が効果が高いという結果になるかもしれません。これがシンプソンの逆説です。このように、全体の傾向だけで判断すると、見落としてしまう重要な情報があるのです。
シンプソンの逆説を理解する事で、情報の分析における注意点や、多角的な視点の大切さを学ぶことができます。より質の高い分析を行うには、データ全体を見るだけでなく、様々なグループに分けて分析したり、他の要因との関係を調べたりする必要があります。
情報に基づいた意思決定がますます重要になる現代社会において、シンプソンの逆説は、情報の分析の専門家だけでなく、全ての人にとって重要な教訓です。私たちは、情報に惑わされず、様々な角度から物事を見る目を養う必要があるでしょう。きちんと情報を分析し、正しい判断をする事で、より良い未来を築く事ができるはずです。
