確率分布:データの宝地図

AIを知りたい
先生、「確率分布」って難しくてよくわからないです。簡単に説明してもらえますか?

AIエンジニア
そうだね、難しく感じるのも無理はないよ。簡単に言うと、確率分布とは、ある出来事が起こる確率をまとめたものなんだ。例えば、サイコロを振ると1から6までの目が出るけど、それぞれの目が出る確率が確率分布だよ。普通のサイコロなら、どの目も1/6の確率で出るよね。

AIを知りたい
なるほど。つまり、どんな結果が起こりやすいかを示しているんですね。でも、確率分布には種類がたくさんあるって聞いたんですが…

AIエンジニア
そう、種類はたくさんあるよ。例えば、コイン投げのように結果がとびとびの値になる場合は「離散型確率分布」と言い、体温を測るように連続的な値になる場合は「連続型確率分布」と言うんだ。他にも色々な種類があるけど、まずはこの2つを押さえておけば大丈夫だよ。
確率分布とは。
人工知能でよく使われる言葉に「確率分布」というものがあります。確率分布とは、ある出来事が起こる確率をまとめた一覧表のようなものです。たとえば、コインを投げたとき、出るのは「表」か「裏」の2通りです。もし、そのコインに細工がなければ、「表」が出る確率も「裏」が出る確率も50%になります。この確率をまとめたものが確率分布です。確率分布にはたくさんの種類があります。データの種類によって、とびとびの値か、連続した値か、扱う値が1つか2つかなどで分けられます。さらに、同じ種類のデータでも、実験や観察の方法によっていくつもの確率分布があります。個数や有る無し、正解か不正解かのように、とびとびの値や状態を扱う場合は「離散型」と呼ばれ、重さや長さ、強さのように連続した量を扱う場合は「連続型」と呼ばれることが多いです。とびとびの値を扱う確率分布として…
確率分布とは

確率分布とは、起こりうる出来事の結果と、その結果が起こる確率を対応させたものです。まるで、宝くじの当選番号と当選金額が書かれた一覧表のようなものだと考えてください。どの結果がどれだけの確率で起こるのかが一目でわかるため、様々な分析に役立ちます。
例として、よく使われるサイコロを振る場合を考えてみましょう。サイコロには1から6までの数字が刻まれており、どの目が出るかは偶然によって決まります。しかし、それぞれの目が出る確率は均等であり、理想的にはどの目も6回に1回の割合で出ると考えられます。この、それぞれの目が出る確率(6分の1)と、出うる目(1から6)を対応させたものが確率分布です。
確率分布は、サイコロのような単純な例に限らず、様々な現象に適用できます。例えば、ある商品の売上の予測や、工場で生産される製品の不良率の推定などにも利用されます。確率分布を用いることで、将来の出来事を予測したり、過去の出来事を分析したりすることが可能になります。
データ分析において、確率分布は重要な役割を担います。データの背後にある規則性や傾向を捉えるために、確率分布は必要不可欠な道具となります。例えば、ある商品の売上のデータを集めたとします。そのデータから売上高の確率分布を作成することで、売上がどれくらいの範囲に収まる可能性が高いか、あるいは売上が大きく変動する要因は何なのかを分析できます。このように、確率分布はデータ分析の基礎となる重要な概念です。
確率分布には様々な種類があり、それぞれの特性に合わせて使い分ける必要があります。代表的なものとしては、正規分布や二項分布などがあります。これらの分布は、それぞれ異なる状況で適用され、データ分析の目的に応じて適切な分布を選択することが重要です。
| 確率分布の概念 | 例(サイコロ) | 応用例 | データ分析における役割 | 種類 |
|---|---|---|---|---|
| 起こりうる出来事の結果とその確率を対応させたもの | それぞれの目(1〜6)が出る確率(1/6) | 商品の売上予測、製品の不良率の推定 | データの背後にある規則性や傾向を捉えるための道具 | 正規分布、二項分布など |
確率分布の種類

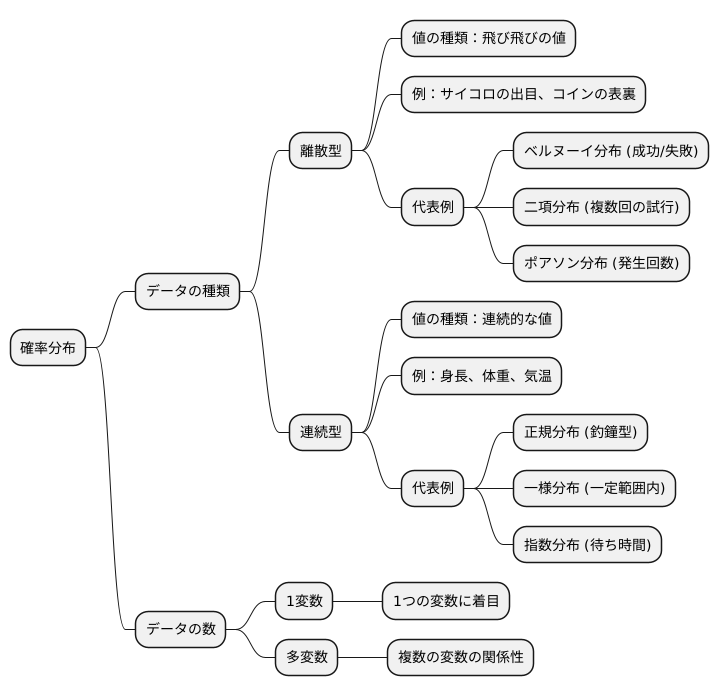
確率分布とは、起こりうる事象それぞれに確率を割り当てたものです。様々な確率分布があり、それらはデータの種類や特性によって使い分けられます。大きくは、値の種類によって離散型と連続型に分けられます。
離散型確率分布は、飛び飛びの値をとるデータを扱う際に用いられます。例えば、サイコロを振った時に出る目の数や、コインを投げた時に表が出る回数などです。代表的な離散型確率分布には、ベルヌーイ分布、二項分布、ポアソン分布などがあります。ベルヌーイ分布は、成功か失敗かのように結果が2つしかない試行を1回行ったときの確率を表します。二項分布は、同じ試行を複数回繰り返したときの成功回数の確率を表します。一方、ポアソン分布は、一定期間に事象が何回起こるかといった、発生回数の確率を表します。このように、離散型確率分布は数えられる値を扱うという特徴があります。
連続型確率分布は、連続的な値をとるデータを扱う際に用いられます。例えば、人の身長や体重、気温など、小数点以下の値を取りうるデータです。代表的な連続型確率分布には、正規分布、一様分布、指数分布などがあります。正規分布は、平均値を中心とした左右対称の釣鐘型の分布で、自然界の多くの現象に当てはまります。一様分布は、一定の範囲内でどの値も同じ確率で発生する分布です。指数分布は、ある事象が次にいつ起こるかといった、待ち時間の確率を表します。このように、連続型確率分布は測ることができる値を扱うという特徴があります。
さらに、扱うデータが1つなのか複数なのかによって、1変数と多変数に分類されます。1変数は1つの変数に着目した分布、多変数は複数の変数の関係性を捉えた分布です。適切な確率分布を選ぶことで、データの背後にある法則を明らかにし、将来の予測に役立てることができます。
離散型確率分布

飛び飛びの値をとるデータ、つまり整数値で表されるデータの確率分布を、離散型確率分布といいます。よくある例としては、サイコロを振って出る目や、お店に来るお客さんの人数などが挙げられます。このような確率分布は、様々な現象を理解し予測するために使われています。
代表的な離散型確率分布として、二項分布とポアソン分布があります。二項分布は、成功か失敗か、表か裏かのように、結果が2つしかない試行を繰り返す場合の確率分布です。例えば、コインを5回投げたときに表が3回出る確率などを計算するために使います。この分布を使うためには、試行の回数と、一回の試行で成功する確率を知る必要があります。
一方、ポアソン分布は、一定の時間や空間の中で、ある出来事が何回起こるかを表す確率分布です。例えば、1時間あたりに銀行の窓口に来るお客さんの人数や、1ページの本の中に誤植がいくつあるかなどを分析する際に用いられます。この分布の特徴は、出来事が起こる平均回数さえ分かれば、その出来事が何回起こるかの確率を計算できる点にあります。
二項分布とポアソン分布は、どちらも離散的なデータを扱う際に非常に役立ちますが、それぞれ適した状況が異なります。試行回数が決まっていて、各試行の結果が独立している場合は二項分布を使い、一方、出来事がランダムに発生し、その平均回数だけが分かっている場合はポアソン分布を使います。これらの確率分布を使い分けることで、様々な現象をより正確に分析し、予測することが可能になります。
| 確率分布の種類 | 説明 | 例 | 必要な情報 |
|---|---|---|---|
| 二項分布 | 結果が2つしかない試行を繰り返す場合の確率分布 | コインを5回投げたときに表が3回出る確率 | 試行回数、1回の試行で成功する確率 |
| ポアソン分布 | 一定の時間や空間である出来事が何回起こるかを表す確率分布 | 1時間あたりに銀行の窓口に来るお客さんの人数、1ページの本の中に誤植がいくつあるか | 出来事が起こる平均回数 |
連続型確率分布

連続型確率分布とは、値が切れ目なく続くデータの確率を表すものです。たとえば、人の身長や体重、気温などは連続的な値をとります。これらの値がどの範囲にどれくらいの確率で現れるのかを示すのが連続型確率分布です。
連続型確率分布の中でも、正規分布は特に重要なものです。正規分布は左右対称な釣鐘型のグラフで表され、平均値を中心とした範囲に多くのデータが集まり、平均値から離れるほどデータの数は少なくなります。自然界の様々な現象、例えば木の葉の大きさや動物の体重、テストの点数などは、正規分布に近い形になることがよくあります。これは、たくさんの小さな偶然が重なって結果が決まる場合に、正規分布が現れやすいからです。
正規分布以外にも様々な連続型確率分布があります。例えば、一様分布は、ある範囲内で全ての値が同じ確率で現れる分布です。これは、例えば乱数を作る時などに利用されます。また、指数分布は、ある事象が起こるまでの時間を表す場合に用いられることが多いです。例えば、電球の寿命や地震の発生間隔などが指数分布に従うことがあります。
連続型確率分布は、連続的なデータを扱う様々な分野で重要な役割を果たしています。例えば、品質管理では製品の寸法のばらつきを分析するために、金融工学では株価の変動を予測するために、医療統計では患者の検査値を評価するために、連続型確率分布が利用されています。これらの分布を理解することで、データの背後にある法則性を明らかにし、より適切な判断を下すことができます。
| 確率分布の種類 | 説明 | 例 | 用途 |
|---|---|---|---|
| 正規分布 | 左右対称な釣鐘型のグラフ。平均値を中心とした範囲に多くのデータが集まる。 | 木の葉の大きさ、動物の体重、テストの点数 | 自然界の様々な現象の分析 |
| 一様分布 | ある範囲内で全ての値が同じ確率で現れる。 | 乱数 | 乱数の生成 |
| 指数分布 | ある事象が起こるまでの時間を表す。 | 電球の寿命、地震の発生間隔 | 事象発生間隔の分析 |
確率分布の活用例

確率分布とは、起こりうる事象それぞれに確率を割り当てたものです。これは、まるで宝くじの当選番号のように、どの番号が出るかは分かりませんが、それぞれの番号が出る可能性は数字で表すことができます。このような確率の分布を表すものが確率分布であり、様々な場面で活用されています。
例えば、商業の場を考えてみましょう。商品の売れ行きを予測する場合、過去の販売データから確率分布を作成することができます。ある商品が1日に10個売れる確率、20個売れる確率、あるいは全く売れない確率などを計算し、分布として表すのです。これにより、今後の売れ行きをある程度の確実性を持って予測することができ、仕入れ量の調整や販売戦略の立案に役立ちます。売れ残りのリスクを減らし、利益を最大化するために、確率分布は欠かせない道具と言えるでしょう。
医療の分野でも確率分布は活躍しています。新しい薬の効果を検証する場合、治験の結果を確率分布を用いて分析します。薬を投与した患者さんと、投与していない患者さんの症状の改善度合いを比較し、薬の効果が偶然によるものなのか、それとも本当に効果があるのかを統計的に判断します。確率分布を用いることで、薬の有効性を客観的に評価することが可能になり、より安全で効果的な治療法の開発に繋がります。
工業製品の製造においても、確率分布は重要な役割を担っています。製品の寿命や故障率を予測するために、確率分布が用いられます。過去の故障データなどを元に、ある製品がどれくらいの期間使えるのか、どのくらいの確率で故障するのかを予測することで、製品の設計やメンテナンス計画を最適化することができます。これにより、製品の安全性や信頼性を高め、顧客満足度を向上させることに繋がります。
このように、確率分布は商業、医療、工業など様々な分野で活用され、データに基づいた的確な判断を助ける強力な道具となっています。確率分布を理解し、活用することで、不確実性の中でも最善の選択をすることができるようになるでしょう。
| 分野 | 確率分布の活用例 | メリット |
|---|---|---|
| 商業 | 商品の売れ行き予測 | 仕入れ量の調整、販売戦略立案、売れ残りリスクの軽減、利益最大化 |
| 医療 | 新薬の効果検証 | 薬の有効性の客観的評価、より安全で効果的な治療法の開発 |
| 工業 | 製品の寿命や故障率予測 | 製品の設計やメンテナンス計画の最適化、製品の安全性や信頼性向上、顧客満足度向上 |
まとめ

確率分布とは、様々な値をとる変数について、それぞれの値が現れる可能性(確率)がどのように分布しているかを示すものです。いわば、データの背後にある隠れた規則性や傾向を明らかにする強力な道具と言えるでしょう。例えば、サイコロを振った時に出る目の確率、ある地域で明日雨が降る確率、商品の売上が特定の範囲に収まる確率など、様々な事象を確率分布で捉えることができます。
確率分布には、正規分布、二項分布、ポアソン分布など、様々な種類が存在します。それぞれの特徴や用途を理解し、データの種類に応じて適切な確率分布を選ぶことが、データ分析の精度を高める鍵となります。例えば、身長や体重といった連続的なデータには正規分布、コイン投げのように結果が成功か失敗かのどちらかしかないデータには二項分布、一定期間内に発生するイベントの回数(例えば、1時間あたりに来店する客の数)にはポアソン分布が用いられます。
確率分布を学ぶことは、データ分析を行う上で非常に重要です。確率分布を用いることで、平均値や分散といった統計量だけでなく、データのばらつきや出現頻度といったより詳細な情報を把握することができます。これは、データに基づいた意思決定を行う際に、より確かな根拠を提供してくれるでしょう。例えば、新商品の需要予測を行う際に、確率分布を用いることで、売上が目標値を達成する確率を算出することができます。
確率分布は、統計学や機械学習といったデータサイエンス分野だけでなく、経済学、物理学、生物学など、様々な分野で応用されています。確率分布を理解することは、データ分析のスキルを向上させるだけでなく、様々な分野の知識を深める上でも役立ちます。データという宝の山を探検するための地図として、確率分布は私たちを導いてくれるでしょう。
| 確率分布の種類 | 特徴 | 用途例 |
|---|---|---|
| 正規分布 | 連続的なデータの分布、身長や体重など | 身長や体重の分布 |
| 二項分布 | 成功か失敗のような二値データの分布、コイン投げなど | コイン投げの結果 |
| ポアソン分布 | 一定期間内に発生するイベントの回数、1時間あたりに来店する客数など | 1時間あたりの来店客数 |
