主成分分析:データの本質を見抜く

AIを知りたい
先生、「主成分分析」って難しそうでよくわからないです。簡単に説明してもらえますか?

AIエンジニア
そうだね、難しく感じるかもしれないね。簡単に言うと、たくさんの情報が詰まったデータを、より少ない情報でなるべく正確に表す方法だよ。例えば、色々な要素で決まるアパートの家賃を、なるべく少ない要素で説明できるようにするようなイメージだね。

AIを知りたい
なんとなくわかった気がします。具体的にはどうやるんですか?

AIエンジニア
例えば、部屋の広さと家賃のデータがたくさんあるとする。広さと家賃には関係性があるよね?つまり、この2つの情報を1つの情報にまとめられる可能性がある。もちろん、情報をまとめるときには、なるべく元の情報の特徴を失わないように工夫する必要があるんだよ。
主成分分析とは。
たくさんの要素で説明されているデータについて、より少ない重要な要素で分かりやすくまとめる方法である「主成分分析」について説明します。例えば、アパートの家賃を考える際に、部屋の広さと家賃のデータがあるとします。これらのデータに関連性があれば、一つの要素でまとめて表現することができます。ただし、このようにデータをまとめると、どうしても元の情報の一部が失われてしまいます。なので、情報をなるべく失わないようにまとめることが大切です。
主成分分析とは

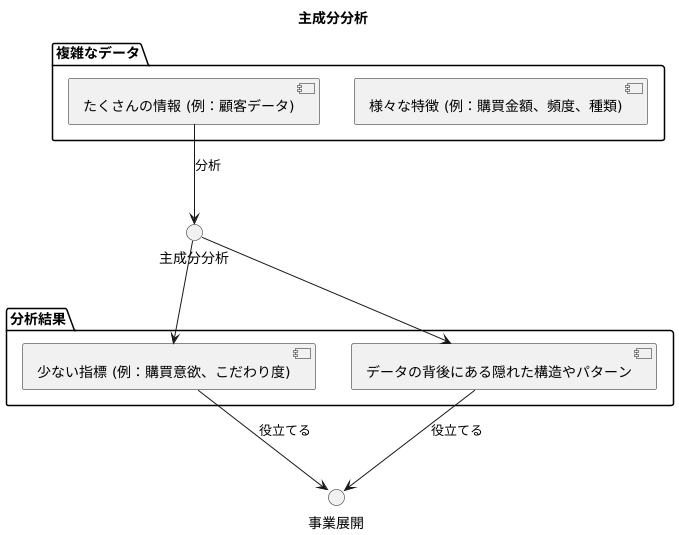
たくさんの情報を持つ複雑なデータを、より少ない指標で分かりやすく表すための方法として、主成分分析というものがあります。これは、統計学に基づいた手法で、データの持つたくさんの特徴を、より少ない重要な特徴にまとめることで、データの背後にある隠れた構造やパターンを見つけ出すことを目的としています。
例として、お店のお客様の買い物に関するたくさんのデータを考えてみましょう。このデータには、お客様がいくら使ったか、どのくらいの頻度で買い物をするか、どんな種類の商品を買っているかなど、様々な情報が含まれています。これらの情報は、それぞれ単独で見ても意味がありますが、たくさんの情報が混ざり合っているため、全体像を把握するのが難しい場合があります。
このような時に主成分分析を使うと、これらの多様な情報を、より少ない数の指標にまとめることができます。例えば、「購買意欲の高さ」や「商品へのこだわり度」といった、少数の指標で顧客の購買行動の主な特徴を表せるようになるのです。これは、まるでたくさんの色を混ぜ合わせて新しい色を作るように、たくさんの情報を組み合わせて、より本質的な情報を抽出する作業に似ています。
この分析は、データの複雑さを軽減し、データの見通しを良くする効果があります。言い換えると、複雑なデータが持つたくさんの軸を、より少ない重要な軸に置き換えることで、データ全体の構造を把握しやすくするのです。これにより、データに隠された重要な情報を見つけやすくなり、今後の事業展開などに役立てることができます。例えば、顧客の購買行動の特徴を掴むことで、効果的な販売戦略を立てることができるようになるでしょう。
次元削減の利点

たくさんの情報を持つデータは、そのままでは扱うのが大変です。次元削減という手法を使うと、データの大切な特徴は保ったまま、扱う情報の量を減らすことができます。これにより、様々な利点が生まれます。
まず、データの内容を絵で見て理解しやすくなります。複雑なデータはそのままでは図にするのが難しいですが、次元削減によって情報量を減らすことで、散布図やグラフといった図でデータの分布やデータ同士の関係を分かりやすく表現できるようになります。まるで霧が晴れたように、データの全体像が掴みやすくなるのです。
次に、計算にかかる時間と手間を省くことができます。たくさんの情報を持つデータを扱う計算は、非常に複雑で時間がかかります。次元削減によって扱う情報量を減らすことで、計算の手間を減らし、処理速度を上げることができます。これにより、分析にかかる時間を大幅に短縮し、より効率的に作業を進めることができます。
さらに、予測の正確さを向上させることができます。たくさんの情報を持つデータには、本来必要のない情報やデータの誤差が含まれていることがよくあります。これらの不要な情報は、予測の正確さを下げてしまう原因となります。次元削減によってこれらの不要な情報を取り除き、本当に必要な情報だけを残すことで、より正確な予測を行うことができるようになります。まるで宝石の原石を磨き上げるように、データの真価を引き出すことができるのです。
| 次元削減の利点 | 説明 |
|---|---|
| データの可視化 | 絵で見て理解しやすくなる。散布図やグラフでデータの分布や関係性を分かりやすく表現できる。 |
| 計算コストの削減 | 計算にかかる時間と手間を省く。処理速度を向上させ、分析時間を短縮できる。 |
| 予測精度の向上 | 不要な情報や誤差を取り除き、必要な情報だけを残すことで、より正確な予測を行うことができる。 |
賃貸物件の例

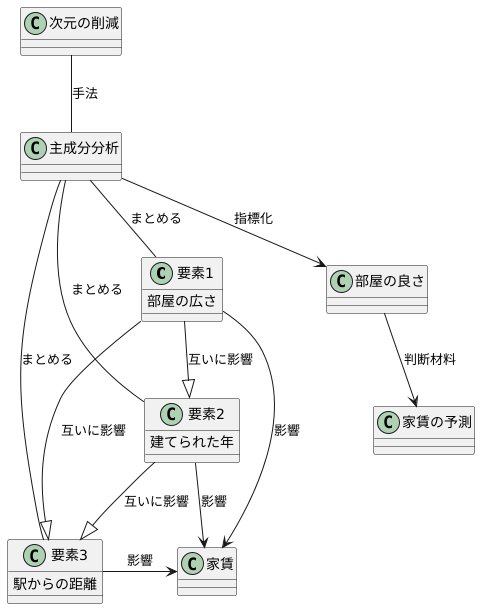
借りられる家の情報を見てみましょう。家賃を決める要素は様々です。部屋の広さ、建てられた年、駅からどのくらい離れているかなど、色々な要素が考えられます。これらの要素は、それぞれがバラバラに家賃を決めているのではなく、互いに影響し合っていることが多いです。例えば、部屋が広ければ広いほど、家賃も高くなる傾向があります。また、駅から近くて新しい建物は、家賃が高くなる傾向があります。
たくさんの要素が複雑に絡み合って家賃が決まる様子を、もっと分かりやすく整理したいときに役立つのが、主成分分析という手法です。主成分分析を使うと、家賃に関係する色々な要素を、「部屋の良さ」といった少数の指標にまとめることができます。この「部屋の良さ」という指標は、家賃に影響を与える主要な要素をうまく反映しています。ですから、部屋を借りるときの大事な判断材料になります。
簡単な例で考えてみましょう。駅から家までの距離と、建てられた年が同じ二つの部屋があるとします。この二つの部屋では、部屋の広さだけで家賃が決まるとしましょう。この場合、家賃を説明する要素は部屋の広さだけなので、たくさんの要素を考えなくても、家賃を予測できます。このように、考える要素の数を減らすことを、次元の削減と言います。主成分分析を使うと、複雑なデータを単純化し、本当に重要な情報だけを取り出すことができます。たくさんの要素が絡み合って分かりにくいデータを、主成分分析によって整理することで、家賃の決まり方をより深く理解できるようになります。
情報の損失とその最小化

情報を扱う上で、情報の損失は避けて通れない問題です。情報をより小さく、扱いやすい形に変換する過程で、どうしても元の情報の一部が削られてしまうからです。例えば、建物の設計図面を縮小コピーする場面を想像してみてください。元の図面には細かい部品の情報まで記載されていますが、縮小コピーされた図面では、これらの詳細な情報は失われてしまいます。
これは、データ分析においても同様です。多くの情報を含むデータを分析する際、全ての情報をそのまま扱うのは困難な場合があります。そこで、重要な情報だけを残し、不要な情報を削ることで、データを扱いやすくする手法が用いられます。この過程で、どうしても情報の損失が発生します。
主成分分析はこの問題に取り組むための強力な手法です。建物の例でいえば、家賃を決める要素は、部屋の広さ、築年数、駅からの距離など様々です。これらの情報を全て考慮すると複雑になりすぎるため、家賃への影響が最も大きい要素、例えば部屋の広さだけに絞り込むことができます。このとき、築年数や駅からの距離といった情報は無視されますが、もしこれらの情報が家賃に与える影響が小さければ、情報の損失は軽微で済みます。
主成分分析では、データのばらつきが最も大きい方向に新しい軸を設定します。データのばらつきが大きい方向は、情報量の多い方向と捉えることができます。この新しい軸を主成分と呼び、この軸に沿ってデータを射影することで、情報の損失を最小限に抑えつつ、次元を削減することができるのです。これは、縮小コピーする際に、重要な情報が含まれる部分をなるべく大きく、詳細な情報が含まれる部分を小さくするように調整する作業に似ています。このように、主成分分析は、情報の損失と簡略化のバランスをうまくとることで、効果的なデータ分析を実現するのです。
| 手法 | 説明 | 例 |
|---|---|---|
| 情報の縮約 | 情報をより小さく、扱いやすい形に変換する過程で、元の情報の一部が削られてしまう。 | 建物の設計図面を縮小コピーする際に、細かい部品の情報が失われる。 |
| データ分析における情報の縮約 | 多くの情報を含むデータを分析する際、重要な情報だけを残し、不要な情報を削ることで、データを扱いやすくする。 | 家賃を決める要素のうち、部屋の広さだけに絞り込む。 |
| 主成分分析 | データのばらつきが最も大きい方向に新しい軸(主成分)を設定し、この軸に沿ってデータを射影することで、情報の損失を最小限に抑えつつ、次元を削減する。 | 家賃への影響が最も大きい要素(部屋の広さ)を抽出し、他の要素を無視する。 |
主成分分析の活用事例

主成分分析は、たくさんの情報をより少ない情報でうまく表すための手法であり、様々な分野で役立っています。膨大なデータの中から重要な情報だけを取り出すことで、データの処理を簡単にするだけでなく、隠れた関係性を見つけることも可能です。
例えば、顔の画像認識を考えてみましょう。一枚の顔画像は、非常に多くの画素情報から成り立っています。これらの画素一つ一つを個別に扱うのは大変ですが、主成分分析を使うことで、顔の形や目鼻立ちといった重要な特徴を少数のパラメータで表現できます。これにより、少ない情報で顔を認識できるようになり、処理速度の向上や認識精度の向上に繋がります。
金融の分野でも主成分分析は活躍しています。株価や為替レートなど、様々な金融商品は複雑に連動しています。主成分分析を用いることで、これらの市場の動きを支配する主要な要因を抽出できます。例えば、市場全体の動向や特定の業界の動向といった主要な要因を把握することで、市場リスクの分析や投資戦略の立案に役立てることができます。
医療の分野では、遺伝子やタンパク質といった膨大な生体情報を扱う際に主成分分析が用いられます。例えば、様々な遺伝子の発現量を測定したデータから、病気の原因となる遺伝子や治療効果を予測する遺伝子を見つけ出すのに役立ちます。さらに、患者の症状や検査データから病気を診断する際にも、主成分分析を用いて重要な情報を絞り込むことで、より正確な診断が可能になります。
このように、主成分分析は、様々な分野でデータの本質を捉え、効率的な分析を可能にする強力な手法です。多くの情報に埋もれて見えにくくなっていた重要な特徴を浮かび上がらせ、問題解決に役立つ情報を提供してくれます。
| 分野 | 説明 |
|---|---|
| 顔画像認識 | 多数の画素情報から顔の形や目鼻立ちといった重要な特徴を少数のパラメータで表現し、少ない情報で顔を認識できるようにする。処理速度の向上や認識精度の向上に繋がる。 |
| 金融 | 株価や為替レートなど、様々な金融商品の動きを支配する主要な要因(市場全体の動向や特定の業界の動向など)を抽出し、市場リスクの分析や投資戦略の立案に役立てる。 |
| 医療 | 遺伝子やタンパク質といった膨大な生体情報から、病気の原因となる遺伝子や治療効果を予測する遺伝子を見つけ出す。患者の症状や検査データから重要な情報を絞り込み、より正確な診断を可能にする。 |
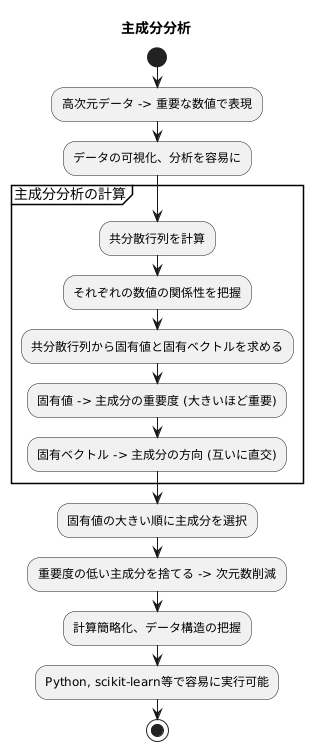
主成分分析の計算方法

主成分分析は、たくさんの数値が入り組んだ高次元データを、より少ない重要な数値で表すための手法です。この手法は、データの持つ情報をなるべく失わずに、複雑さを軽減することで、データの可視化や分析を容易にすることを目的としています。では、どのようにして重要な情報を選び出すのでしょうか。
主成分分析の計算は、行列とベクトルを用いた線形代数という数学の分野に基づいています。手順としては、まず分析対象となるデータのばらつき具合を表す共分散行列を計算します。この行列は、それぞれの数値が互いにどのように関係しているかを示しています。共分散行列から、固有値と固有ベクトルと呼ばれる特別な値とベクトルを求めます。固有値は、それぞれの主成分がどれだけの情報を持ち合わせているか、つまり重要度を表す数値です。固有値が大きいほど、その主成分がデータのばらつきをより多く説明できることを意味します。固有ベクトルは、新しい座標軸、すなわち主成分の方向を示すベクトルです。これらの固有ベクトルは互いに直交しており、独立した方向を示しています。
一般的には、固有値の大きい順に主成分を選択します。固有値が大きい主成分から順番に採用することで、データの持つ情報を効率的に捉えることができます。そして、重要度の低い主成分を捨てることで、データの次元数を削減します。必要な情報の大部分が残るように、次元数を減らすことで計算を簡略化し、データの構造を把握しやすくします。
数式を用いて具体的な計算を行うのは少々複雑ですが、幸いなことに、多くの統計処理を行うための計算機プログラムやプログラミング言語の追加機能には、主成分分析を行うための便利な道具が用意されています。例えば、パイソンというプログラミング言語のサイキットラーンという追加機能には、主成分分析を行うための関数が含まれており、ほんの数行の記述で実行できます。そのため、計算の細部まで理解していなくても、容易に主成分分析を活用することができます。