重回帰分析:複数の要因から未来を予測

AIを知りたい
先生、重回帰分析って難しそうでよくわからないのですが、簡単に説明してもらえますか?

AIエンジニア
そうだな、たとえばアイスクリームの売上を考えよう。気温が上がると売上も上がるよね?これは単回帰分析でわかる関係だ。でも、気温だけでなく、曜日や近所のイベントなども売上に関わってくるよね?重回帰分析は、このような複数の要素がどう売上に影響するかを調べる方法なんだ。

AIを知りたい
なるほど。複数の要素が関係するんですね。つまり、アイスクリームの売上を予測するには、気温だけでなく曜日やイベントの情報も必要ということですか?

AIエンジニア
その通り!重回帰分析を使えば、複数の要素を考慮してより正確な予測ができるようになるんだ。気温や曜日、イベントの情報などから、どれがどれくらい売上に影響しているかを分析し、将来の売上を予測することができるんだよ。
重回帰分析とは。
複数のデータが互いにどのように関係しているかを明らかにする統計的な方法の一つに『回帰分析』というものがあります。
例えば、ある事柄について、一つの原因となるデータから結果を予測する分析を『単回帰分析』と呼びます。
一方、結果に影響を与える原因となるデータが複数ある場合、それらの関係性を分析するのが『重回帰分析』です。
この『重回帰分析』を使うことで、何がどの程度影響を与えているのかという要因の分析や、今後の予測に役立てることができます。
関係性を明らかにする統計手法

わたしたちの身の回りでは、様々な出来事が複雑に絡み合いながら起こっています。一つの結果には、多くの要素が影響を与えていることがほとんどです。例えば、ある商品の売れ行きを考えてみましょう。売れ行きは商品の値段だけで決まるわけではありません。宣伝にかけた費用や季節、競合する商品の状況など、様々な要素が複雑に影響し合っているはずです。これらの要素が、売れ行きにどれほど影響しているのか、また、それぞれの要素同士はどのような関係にあるのかを数値的に明らかにする統計的な方法の一つが、重回帰分析です。
重回帰分析は、複数の説明変数と呼ばれる要素を用いて、目的変数と呼ばれる結果を説明しようとする手法です。先ほどの商品の売れ行きの例で言えば、宣伝費用、季節、競合商品の状況などが説明変数、売れ行きが目的変数となります。重回帰分析を行うことで、それぞれの説明変数が目的変数にどれくらい影響を与えているかを数値化することができます。例えば、宣伝費用を1万円増やすと売れ行きはどれくらい増えるのか、夏は冬に比べてどれくらい売れ行きが変わるのかといったことを具体的に示すことができます。
重回帰分析によって得られた数値は、それぞれの要素の影響の大きさを比較したり、どの要素が最も重要なのかを判断するのに役立ちます。また、これらの数値を用いて将来の予測を行うことも可能です。例えば、来年の宣伝費用をいくらに設定すれば、目標の売れ行きを達成できるのかを予測することができます。
このように、重回帰分析は複雑な現象を理解し、将来を予測するための強力な道具となります。ビジネスの意思決定から科学的な研究まで、幅広い分野で活用されています。ただし、重回帰分析を行う際には、データの質や分析方法の妥当性などに注意する必要があります。適切なデータを用い、正しい手順で分析を行うことで、より正確で信頼性の高い結果を得ることができます。
| 項目 | 説明 |
|---|---|
| 重回帰分析 | 複数の説明変数(要素)を用いて、目的変数(結果)を説明する統計的手法。それぞれの説明変数が目的変数にどれくらい影響を与えているかを数値化。 |
| 説明変数 | 結果に影響を与える要素。例:商品の売れ行きにおける宣伝費用、季節、競合商品の状況など |
| 目的変数 | 説明変数によって説明される結果。例:商品の売れ行き |
| 重回帰分析の利点 |
|
| 重回帰分析の注意点 | データの質や分析方法の妥当性に注意が必要 |
| 活用例 | ビジネスの意思決定、科学的な研究など幅広い分野 |
単回帰分析との違い

単回帰分析と重回帰分析は、どちらも統計学においてデータの関係性を分析し、予測を行うために用いられる手法ですが、説明変数の数に大きな違いがあります。
単回帰分析は、一つの説明変数を使って目的変数を予測します。例えば、気温の変化からアイスクリームの売上高を予測する場合を考えてみましょう。気温が高くなればアイスクリームの売上も増えるという関係性を仮定し、過去の気温と売上高のデータから、売上高を気温の関数として表す式を作成します。この式を用いれば、未来の気温からアイスクリームの売上高を予測することができます。まるで、気温という一つの要素だけで売上が決まるかのように扱います。
しかし、現実世界ではアイスクリームの売上高は気温以外にも様々な要因に影響を受けます。例えば、曜日、近隣でのイベント開催の有無、近隣の学校の夏休み期間、近年のアイスクリームの人気度なども考えられます。このような複数の要因を考慮するのが重回帰分析です。
重回帰分析では、複数の説明変数を用いて目的変数を予測します。つまり、アイスクリームの売上高を予測する際に、気温だけでなく、曜日やイベント開催の有無なども考慮することで、より現実に近い、精度の高い予測が可能になります。複数の説明変数を用いることで、単回帰分析では捉えきれなかった複雑な関係性を分析し、より正確な予測を行うことができるのです。
このように、単回帰分析は一つの要因に着目したシンプルな分析手法である一方、重回帰分析は複数の要因を考慮した、より複雑な分析手法と言えます。扱うことができる情報の量が違うため、重回帰分析はより現実に近い複雑な現象を扱うことができ、幅広い分野で活用されています。
| 項目 | 単回帰分析 | 重回帰分析 |
|---|---|---|
| 説明変数の数 | 1つ | 複数 |
| 目的変数 | 1つ | 1つ |
| 例 | 気温 → アイスクリームの売上高 | 気温、曜日、イベント開催の有無など → アイスクリームの売上高 |
| 特徴 | シンプルな分析手法 | 複雑な関係性を分析可能 |
| 予測精度 | 限定的 | 単回帰分析より高い |
要因分析による理解

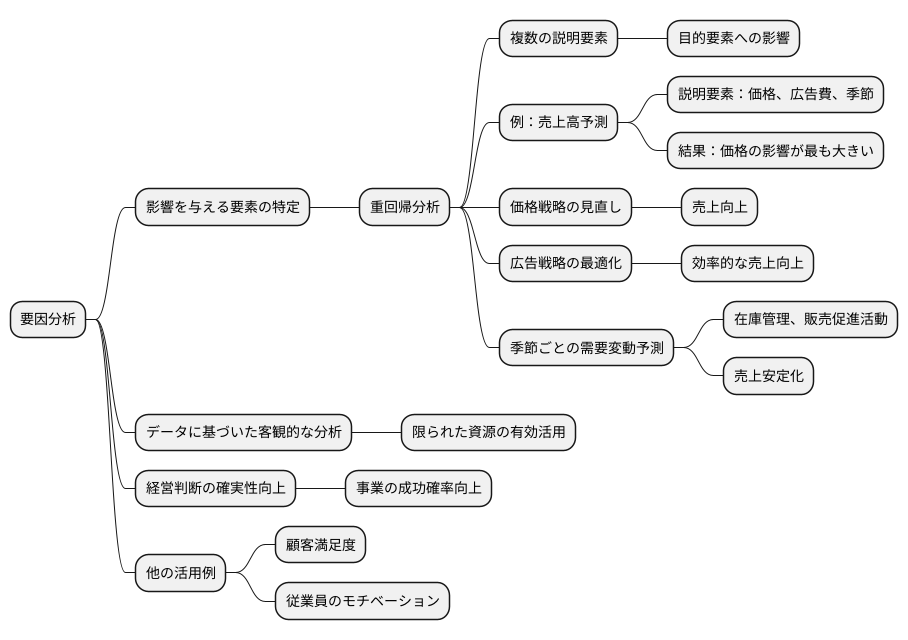
要因分析とは、ある事柄に影響を与える様々な要素の中から、特に重要な要素を見つけ出す手法です。この分析には、重回帰分析がよく用いられます。重回帰分析は、複数の説明要素が目的要素にどのように影響するかを分析する統計手法です。つまり、様々な要素の中から、どれが目的の事柄に最も大きな影響を与えているのかを明らかにすることができます。
例えば、商品の売上高を予測する場合を考えてみましょう。売上に影響を与える要素として、商品の価格、広告費、季節などが考えられます。これらの要素を説明要素として重回帰分析を行うことで、どの要素が売上に最も大きく影響しているかを数値化することができます。分析の結果、価格が最も大きな影響力を持っていると判明した場合、価格戦略の見直しによって売上向上を図ることが有効だと考えられます。また、広告費の影響が大きいとわかった場合は、広告戦略の最適化に注力することで、より効率的な売上向上を目指すことができます。季節の影響が大きい場合は、季節ごとの需要変動を予測し、在庫管理や販売促進活動を調整することで、売上の安定化を図ることができます。
このように、重回帰分析を用いた要因分析は、どの要素に重点的に資源を投入すべきかを判断するための重要な材料となります。限られた資源を効果的に活用するためには、データに基づいた客観的な分析が不可欠です。要因分析によって得られた知見は、経営判断をより確かなものにし、事業の成功確率を高めるために役立ちます。さらに、要因分析は売上予測以外にも、顧客満足度や従業員のモチベーションなど、様々な場面で活用できます。分析対象と説明要素を適切に設定することで、複雑な事象を理解し、より良い意思決定を行うための強力なツールとなるのです。
予測分析による未来予測

未来を見通すことは、昔から人々の願いでした。天気予報のように身近なものから、経済の動向といった大きなものまで、未来が分かれば、それに合わせて準備ができます。近年、多くの情報が集められるようになり、この情報を活用した未来予測の手法に注目が集まっています。それが予測分析です。
予測分析とは、過去のデータから規則性や傾向を見つけ出し、未来の状態を推定する手法です。様々な方法がありますが、中でも重回帰分析は有力な手段の一つです。重回帰分析とは、複数の要因が結果にどう影響するかを分析する方法です。例えば、商品の売上を予測したいとします。売上に影響する要素は様々です。商品の値段、広告費、季節、競合商品の有無など、多くの要素が考えられます。重回帰分析を用いると、これらの要素がそれぞれどれくらい売上に影響を与えているかを数値化できます。
過去の売上データと、それに対応する値段、広告費、季節などのデータを分析することで、売上と各要素の関係を表す数式を作ることができます。この数式のことを「重回帰モデル」と呼びます。一度このモデルを作れば、未来の予測に役立ちます。例えば、来月の売上を予測したい場合、来月の値段、広告費、季節を予測し、モデルに当てはめることで、来月の売上を予測できます。
未来の予測は、事業計画を立てる上で非常に重要です。売上予測に基づいて生産量や仕入れ量を調整したり、必要な人員を計画したりできます。また、リスク管理にも役立ちます。例えば、ある商品の売上が大きく落ち込むと予測された場合、事前に対策を考え、実行することで、損失を最小限に抑えることができます。予測分析は、不確実な未来に対する備えとなり、より良い判断材料を提供してくれるのです。
| 項目 | 説明 |
|---|---|
| 予測分析 | 過去のデータから規則性や傾向を見つけ出し、未来の状態を推定する手法 |
| 重回帰分析 | 複数の要因が結果にどう影響するかを分析する方法。予測分析の一種。 |
| 重回帰モデル | 売上と各要素の関係を表す数式。過去のデータから作成。 |
| 予測分析の活用例 | 事業計画(生産量/仕入れ量の調整、人員計画)、リスク管理(損失の最小化) |
| 重回帰分析の例 | 商品の売上予測(値段、広告費、季節、競合商品の有無などから予測) |
様々な分野への応用

重回帰分析は、多くの分野で活用されている強力な分析手法です。
経済学の分野では、経済成長に影響を与える様々な要因を分析するために用いられています。例えば、国の経済成長率を目的変数とし、資本投入、労働投入、技術革新などを説明変数として、それぞれの要因が経済成長にどの程度寄与しているかを分析することができます。また、過去の株価データや経済指標などを説明変数として、将来の株価を予測するのにも利用されています。
経営学においては、企業の売上予測などに活用されています。例えば、過去の売上データ、広告費、景気指標などを説明変数として、将来の売上高を予測することで、企業の経営戦略策定に役立てることができます。顧客満足度調査の結果を分析し、顧客満足度に影響を与える要因を特定することで、サービスの改善にも繋がります。
社会学の分野では、犯罪の発生率や、貧困、教育格差といった社会問題の分析に役立っています。例えば、地域の人口密度、失業率、教育水準などを説明変数として、犯罪発生率との関連性を分析することで、犯罪発生のメカニズムの解明や、効果的な犯罪対策の立案に貢献することができます。
医学の分野では、病気の発症リスクを予測するために活用されています。例えば、生活習慣、遺伝情報、環境要因などを説明変数として、特定の病気を発症する確率を予測することで、病気の予防や早期発見に繋がります。また、新薬の開発においては、薬の効果を検証するために重回帰分析が用いられることもあります。
このように、重回帰分析は、様々な分野の研究や実務において、データに基づいた意思決定を支援する上で、重要な役割を担っています。
| 分野 | 目的変数 | 説明変数 | 活用例 |
|---|---|---|---|
| 経済学 | 経済成長率 | 資本投入、労働投入、技術革新など | 経済成長への要因分析、株価予測 |
| 経営学 | 売上高 | 過去の売上データ、広告費、景気指標など | 売上予測、顧客満足度分析 |
| 社会学 | 犯罪発生率 | 人口密度、失業率、教育水準など | 犯罪発生メカニズムの解明、犯罪対策立案 |
| 医学 | 特定の病気の発症確率 | 生活習慣、遺伝情報、環境要因など | 病気の予防、早期発見、新薬開発 |
複雑な現実への適用

現実の世界で起こる問題は、単純なものではなく、いくつもの要因が複雑に絡み合っていることがほとんどです。例えば、商品の売り上げを考えてみましょう。売り上げは、商品の値段だけでなく、広告の量、季節、競合商品の状況など、様々な要素に影響を受けます。このような複雑な現実を理解し、将来を予測するために役立つのが重回帰分析です。
重回帰分析は、複数の説明変数を同時に考慮することで、現実世界の問題をより正確に捉えることができます。先ほどの商品の売り上げの例で言えば、値段、広告費、季節、競合商品のデータなどを説明変数として用いることで、それぞれの要素が売り上げにどう影響するかを調べ、より現実に近いモデルを作ることができます。つまり、重回帰分析を使えば、複雑な現象を紐解き、それぞれの要因の影響度合いを数値化できるのです。
もちろん、重回帰分析にも注意点はあります。分析に使うデータの質が悪いと、正確な結果を得ることができません。データに偏りがあったり、重要な情報が欠けていたりすると、分析結果の信頼性が低下してしまいます。また、分析に使うモデルが適切でなければ、現実に合わない結果が出てしまう可能性があります。例えば、関係のない変数をモデルに含めてしまったり、データの特性に合わないモデルを使ったりすると、誤った結論を導きかねません。
しかし、これらの注意点に気を付けて、データの質を高め、適切なモデルを選択すれば、重回帰分析は非常に強力なツールとなります。複雑な現象の理解を深め、将来の予測精度を高めることができるため、経済学、社会学、医学など、様々な分野で広く活用されています。適切な使い方を理解し、その長所を活かすことで、私たちは複雑な現実をより深く理解し、より良い意思決定を行うことができるようになるのです。
| 項目 | 説明 |
|---|---|
| 重回帰分析の目的 | 複雑に絡み合った複数の要因が結果に及ぼす影響を分析し、将来を予測する |
| 仕組み | 複数の説明変数を用いて、それぞれの要因の影響度合いを数値化 |
| 例 | 商品の売り上げ予測(値段、広告費、季節、競合商品データなどを説明変数として使用) |
| 注意点 | データの質、モデルの適切さが重要。偏りや欠損のあるデータ、不適切なモデルの使用は、信頼性低下や誤った結論につながる |
| メリット | 複雑な現象の理解、将来予測精度の向上 |
| 活用分野 | 経済学、社会学、医学など |
