多次元尺度構成法:データの視覚化

AIを知りたい
先生、「多次元尺度構成法」って難しそうでよくわからないんですけど、簡単に教えてもらえますか?

AIエンジニア
そうだね、難しく感じるかもしれないね。簡単に言うと、たくさんの性質を持つデータ同士の関係性を、できるだけ保ったまま、少ない情報で表現する方法なんだ。たとえば、果物を甘さや色、大きさなどで比べたときに、似たもの同士を近くに配置した地図を作るようなイメージだよ。

AIを知りたい
果物の地図ですか?なんとなくイメージが湧いてきました!でも、何のためにそんなことをするんですか?

AIエンジニア
良い質問だね。たくさんの性質をそのまま扱うのは大変だから、少ない情報にまとめることで、データの特徴や関係性を分かりやすくしたり、分析しやすくしたりすることができるんだよ。例えば、果物の地図で言えば、似た味の果物を見つけやすくなるよね。
多次元尺度構成法とは。
人工知能でよく使われる言葉に「多次元尺度構成法」というものがあります。これは、主成分分析のように、たくさんの次元を持つデータをより少ない次元で表すための方法のひとつです。この方法では、もとのデータ同士がどれくらい近いか、あるいは似ているかという関係を保ったまま、次元を減らします。結果として、似た性質を持つデータは近くに集まって配置された図が得られます。
手法の概要

多次元尺度構成法とは、たくさんの情報を持つデータの見方を分かりやすく整理するための手法です。高次元、つまり多くの要素で構成されたデータの関係性を、二次元や三次元のような低い次元に変換することで、視覚的に捉えやすくします。まるで、複雑な地図を簡略化して見やすくするようなものです。
例えば、様々な商品に対する消費者の評価データを考えてみましょう。それぞれの商品には、価格、品質、デザインなど多くの要素があり、これらの要素を基に消費者は商品を評価します。この評価データは、そのままでは複雑で理解しづらい高次元データです。しかし、多次元尺度構成法を用いることで、この複雑なデータを二次元の平面上に配置することができます。似た評価を得た商品は近くに、異なる評価の商品を遠くに配置することで、商品の位置関係から消費者の好みを視覚的に把握することが可能になります。
都市間の距離データも、多次元尺度構成法が有効に活用できる例です。各都市間の距離は、直線距離だけでなく、交通網の発達状況や地理的な条件など様々な要因が複雑に絡み合っています。これらの要因を全て考慮した高次元データは、そのままでは理解しにくいため、多次元尺度構成法を用いて二次元平面上に都市を配置します。実際の地図とは異なるかもしれませんが、都市間の近さ、遠さの関係性を視覚的に表現することで、都市間の繋がりや地理的な特徴を新たな視点から捉えることができます。
このように、多次元尺度構成法は、高次元データに隠された関係性を分かりやすく表現し、データの可視化を通じて新たな発見を促す強力な手法と言えるでしょう。
| 手法 | 目的 | 方法 | 例 | 効果 |
|---|---|---|---|---|
| 多次元尺度構成法 | 高次元データを見やすく整理し、理解しやすくする | 高次元データを低次元(2次元や3次元)に変換し、視覚的に表現 |
|
データに隠された関係性を分かりやすく表現し、新たな発見を促す |
主成分分析との違い

たくさんの情報を持つ複雑なデータは、そのまま扱うのが難しい場合があります。そこで、情報をなるべく損なわずに、もっと単純な形に変換する方法が求められます。このような方法を次元削減と呼び、色々な手法が考えられています。主成分分析と多次元尺度構成法も、この次元削減の手法です。どちらもデータの次元を減らすという目的は同じですが、そのやり方や重視する点が違います。
主成分分析は、データが持つ情報のばらつき具合、つまり分散に注目します。データが色々なところに散らばっている様子を、できるだけうまく捉えられるような新しい軸を探します。そして、この新しい軸を使ってデータを表現することで、元の複雑なデータから重要な情報だけを抜き出し、次元を減らします。たくさんの軸の中から、情報のばらつきが最も大きい方向の軸を最初の軸として選び、次にその軸とは関係なく、情報のばらつきが大きい方向の軸を選びます。これを繰り返すことで、情報の損失を最小限にしながら次元数を減らしていきます。
一方、多次元尺度構成法は、データ同士の近さ、または似たり寄ったり具合を保つことを重視します。元のデータで近い関係にあるデータは、次元を減らした後も近くに配置されるようにします。元のデータで遠い関係にあるデータは、次元を減らした後も遠くに配置されるようにします。つまり、多次元尺度構成法は、データの全体的な位置関係をなるべく正確に表現できるような低い次元の空間を探し、そこにデータを配置することで次元削減を行います。
このように、主成分分析はデータのばらつきに着目し、多次元尺度構成法はデータ間の関係性に着目します。扱うデータの種類や分析の目的によって、どちらの手法が適しているかが変わるため、状況に応じて適切な手法を選ぶことが大切です。
| 手法 | 目的 | 重視する点 | やり方 |
|---|---|---|---|
| 主成分分析 | 次元削減 | データのばらつき(分散) | 情報のばらつきが大きい方向の軸を新しい軸として選び、次元を減らす |
| 多次元尺度構成法 | 次元削減 | データ間の近さ、類似性 | データ間の関係性を保つように低次元空間にデータを配置する |
手法の種類

多次元尺度構成法には、大きく分けて二つの種類があります。一つは計量多次元尺度構成法、もう一つは非計量多次元尺度構成法です。これらの手法は、扱うデータの種類によって使い分けられます。
計量多次元尺度構成法は、対象間の距離が数値で正確に測れる場合に適しています。例えば、日本の各都市間の距離を地図上で測ったデータなどが挙げられます。これらのデータは数値で明確に表されているため、そのまま分析に用いることができます。都市間の距離だけでなく、工場における機械同士の配置間隔や、スーパーマーケットの商品棚の距離なども、計量多次元尺度構成法に適したデータです。計量多次元尺度構成法を使うことで、これらの数値データから対象間の関係性を視覚的に把握することができます。
一方、非計量多次元尺度構成法は、対象間の距離が数値で測れない場合に用います。例えば、複数の人にある商品に対する好き嫌いを尋ね、それぞれの類似度を評価してもらったとします。この場合、得られるデータは数値ではなく、類似している、少し類似している、類似していないといった順序データになります。また、複数の写真を見比べて、どの写真がより似ているかを判断する場合なども、順序データとして扱われます。このように、数値で直接測れない、対象間の類似性や好みといったデータは、非計量多次元尺度構成法を用いて分析します。非計量多次元尺度構成法では、これらの順序データを基に、対象間の関係性を低次元空間上に表現することで、視覚的に分かりやすく示してくれます。
このように、多次元尺度構成法はデータの種類に合わせて適切な手法を選ぶことが大切です。分析したいデータが数値で正確に測れるものか、それとも順序データなのかを見極めることで、より正確で有益な分析結果を得ることができます。
| 手法 | データの種類 | 例 |
|---|---|---|
| 計量多次元尺度構成法 | 数値データ (距離) | 都市間の距離、機械の配置間隔、商品棚の距離 |
| 非計量多次元尺度構成法 | 順序データ (類似度、好み) | 商品に対する好き嫌い、写真の類似度 |
応用例

多次元尺度構成法は、様々な分野で活用されている、データ分析のための強力な手法です。
まず、市場の動向を探る分野では、商品どうしの似ているところを調べ、競合する商品を見つけるのに役立ちます。例えば、清涼飲料水について、味や価格、広告イメージといった様々な側面から見て、どの商品が互いに似ているかを分析します。この分析結果を基に、自社製品とよく似た商品、つまり競合商品を特定し、市場における自社製品の位置づけを明確にすることができます。さらに、新たな商品の開発においても、消費者の好みに合わせた、最適な位置づけを見つけるために活用できます。
次に、心の動きを探る分野では、人のイメージや感覚といった、数値化しにくいデータを分析するのに役立ちます。例えば、被験者にいくつかの単語を提示し、それぞれの単語から感じる印象を評価してもらいます。「温かい」「冷たい」「明るい」「暗い」といった尺度を用いて評価することで、それぞれの単語が持つイメージを多次元空間上に配置することができます。この配置から、単語間の心理的な距離や関係性を視覚的に把握し、人の心の奥にあるイメージ構造を明らかにすることができます。
さらに、生き物のつながりを探る分野でも、多次元尺度構成法は力を発揮します。生物の遺伝情報の違いを数値化し、その数値に基づいて生物種間の近さを分析します。似ている遺伝情報を持つ生物種は近くに配置され、遠い生物種は遠くに配置されます。こうして、生物種間の進化の道筋を視覚化した系統樹を作成することができます。
このように、多次元尺度構成法は、市場調査、心理学研究、生物学研究など、多様な分野で活用できる汎用性の高い分析手法と言えるでしょう。
| 分野 | 活用例 | 目的 |
|---|---|---|
| 市場の動向を探る | 清涼飲料水の味、価格、広告イメージの類似性を分析 | 競合商品特定、自社製品の位置づけ明確化、新商品の最適な位置づけ決定 |
| 心の動きを探る | 単語から感じる印象を「温かい」「冷たい」「明るい」「暗い」等の尺度で評価し、多次元空間上に配置 | 単語間の心理的な距離や関係性把握、イメージ構造の解明 |
| 生き物のつながりを探る | 生物の遺伝情報の違いを数値化し、生物種間の近さを分析 | 生物種間の進化の道筋を視覚化した系統樹の作成 |
データの解釈

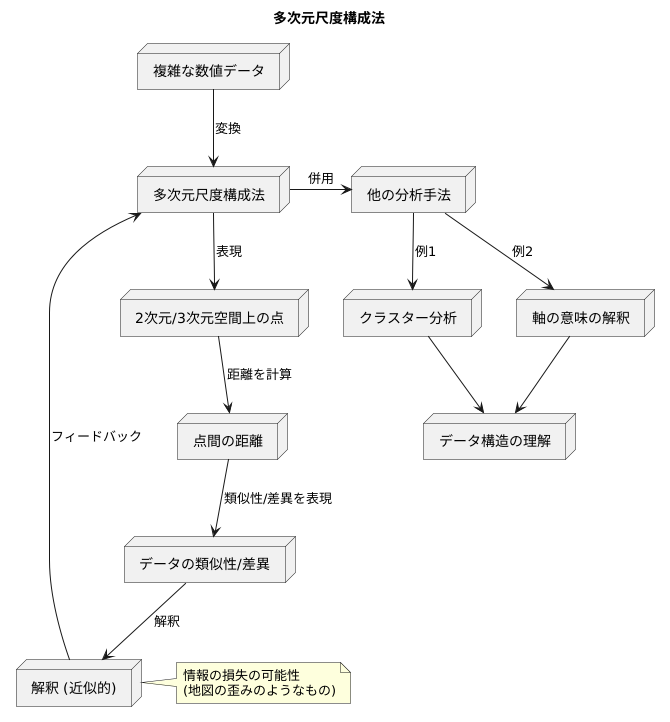
たくさんの数値が並んだ複雑なデータは、そのままでは全体像をつかむのが難しいものです。そこで、多次元尺度構成法という手法を用いて、複雑なデータを分かりやすい図として表現することができます。
この手法は、元々たくさんの数値で表されていたデータの関係性を、2次元や3次元といった少ない数の軸で表現できるよう変換するものです。変換後のデータは、まるで地図上に配置された地点のように、点として図示されます。
図の中の点と点の距離が近いほど、元のデータは似ていることを示します。逆に、点と点の距離が遠いほど、元のデータは異なっていると解釈できます。例えば、顧客の購買データを分析する場合、似たような商品を購入する顧客は近くに配置され、全く異なる商品を購入する顧客は互いに遠く離れて配置されるでしょう。
しかし、多次元尺度構成法は、複雑な情報を単純化して表現するため、元のデータが持っていた情報の一部は失われてしまう可能性があります。地図を作る際に、地球の表面を平面の地図に置き換えると、どうしても歪みが生じてしまうのと似ています。そのため、図から得られた解釈は、あくまで近似的なものだと理解しておく必要があります。
多次元尺度構成法だけでデータのすべてを理解することは難しいため、他の分析手法と組み合わせて使うことが重要です。例えば、点のグループ分けを行うクラスター分析と組み合わせることで、似た性質を持つデータの集団を見つけることができます。また、それぞれの軸がどのような意味を持つのかを他の分析手法を用いて詳しく調べることで、データの構造に対する理解をさらに深めることができます。
まとめ

たくさんのデータが複雑に絡み合った様子を、分かりやすく整理して見せてくれるのが、多次元尺度構成法です。この手法は、高次元、つまりたくさんの特徴を持つデータを、二次元や三次元といった低い次元の空間に配置することで、データ全体の構造を把握しやすくします。複雑なデータを分かりやすく図示することで、隠れた関係性を見つけ出すことができるのです。
例えば、様々な商品の販売データがあるとします。それぞれの商品の価格、販売数、顧客層など、たくさんの情報があります。これらの情報を多次元尺度構成法を用いて分析すると、似た特徴を持つ商品が近くに配置され、グループ分けされます。どの商品が売れ筋なのか、どの商品同士が競合しているのか、視覚的に理解できるようになります。
この手法は、似た手法である主成分分析とは少し違います。主成分分析はデータ全体のばらつきをなるべく維持するように次元を削減しますが、多次元尺度構成法はデータ同士の距離や類似度といった関係性をなるべく保つように次元を削減します。つまり、元のデータで近い関係にあったデータは、低次元空間でも近くに配置されるように工夫されているのです。
多次元尺度構成法には、大きく分けて計量的手法と非計量的手法があります。計量的手法は、データが数値で表される場合に用いられます。例えば、都市間の距離や商品の価格差などです。一方、非計量的手法は、データが数値ではない場合に用いられます。例えば、商品の好き嫌いといった、数値で表しにくいデータです。分析するデータの種類に合わせて、適切な手法を選ぶ必要があります。
多次元尺度構成法は、様々な分野で活用されています。商品の市場調査を行うマーケティング分野、人の心理を探る心理学分野、生物の遺伝子情報を分析する生物学分野など、応用範囲は多岐に渡ります。データの可視化を通じて、新たな発見を促す強力な手法として、データ分析を行う上で非常に役立ちます。
| 項目 | 説明 |
|---|---|
| 多次元尺度構成法 | 高次元データを低次元空間に配置し、データ全体の構造を把握しやすくする手法。 |
| 目的 | 複雑なデータの可視化、隠れた関係性の発見。 |
| 例 | 商品の販売データ(価格、販売数、顧客層など)を分析し、商品間の関係性を視覚的に理解する。 |
| 主成分分析との違い | 主成分分析はデータ全体のばらつきを維持するように次元削減するが、多次元尺度構成法はデータ間の距離や類似度を維持するように次元削減する。 |
| 手法の種類 | 計量的手法(数値データ)、非計量的手法(非数値データ) |
| 活用分野 | マーケティング、心理学、生物学など |
