クラスター分析:データの類似性を見つける

AIを知りたい
先生、クラスター分析って、階層クラスター分析と非階層クラスター分析の2種類があるって習ったんですけど、違いがよくわからないんです。

AIエンジニア
なるほど。では、果物を例に考えてみよう。階層クラスター分析は、例えば、りんご、みかん、ぶどう、バナナがあったとして、まず、形や色が似ているりんごとめろんをグループにする。次に、ぶどうとバナナをグループにする。最後に、これら2つのグループをまとめてさらに大きなグループにする、といった具合に、似ているものから順に階層的にまとめていく方法だよ。

AIを知りたい
あ〜、だんだんわかってきました。じゃあ、非階層クラスター分析はどういうものですか?

AIエンジニア
非階層クラスター分析は、最初にいくつのグループに分けるかを決めておくんだ。例えば、果物を3つのグループに分けると決めて、形や色、味などで似たもの同士をグループ分けしていく。階層のようにグループをまとめたりはしないんだ。
クラスター分析とは。
人工知能でよく使われる「集団分けの分析」には、大きく分けて二つのやり方があります。一つは「段階的な集団分け」で、似ているもの同士を順番にまとめていく方法です。もう一つは「段階的ではない集団分け」で、名前の通り、段階を作らずに集団を分ける方法です。
はじめに

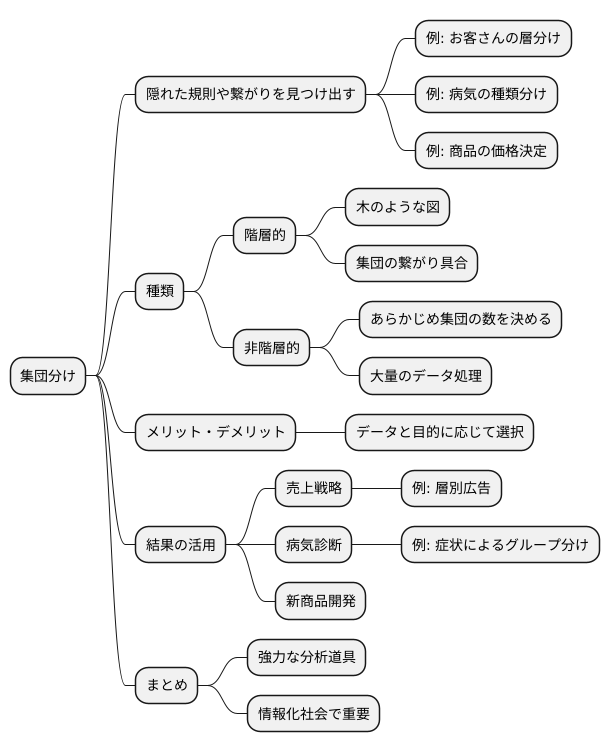
似通った性質を持つものの集まりを作る方法、それが集団分けのやり方です。たくさんのデータから、隠れた規則や繋がりを見つけ出すために、様々な場所で役立っています。
例えば、お店でお客さんが買った品物の記録を調べ、お客さんの層を分けたり、遺伝子の働き方から病気の種類を分けたり、商品の性質を調べて値段を決めるなど、色々な場面で使われています。
この集団分けのやり方は、大きく分けて二つの種類があります。一つは階層的な方法、もう一つは非階層的な方法です。階層的な方法は、木のような図を使って、似たものを順々にまとめていくやり方です。それぞれの集団の繋がり具合がよく分かります。非階層的な方法は、あらかじめ集団の数を決めて、決めた数の集団に分けていくやり方です。たくさんのデータを扱う時に向いています。
どちらの方法にも、それぞれに良い点と悪い点があります。扱うデータの種類や目的によって、適切な方法を選ぶことが大切です。
この集団分けのやり方で分けた結果を元に、お店で売るための作戦を立てたり、病気の診断を助けたり、新しい商品を作ったりと、色々な場面で役立ちます。
例えば、お客さんをいくつかの層に分け、それぞれの層に合った広告を出すことで、より効果的に商品を売ることができます。また、病気の患者さんを症状によってグループ分けすることで、より正確な診断や治療法の選択に繋がります。
このように、データの分析において、集団分けのやり方は、隠れた情報を見つけ出すための強力な道具と言えるでしょう。大量のデータの中から意味のある情報を抽出する技術は、これからの情報化社会においてますます重要になっていくと考えられます。
クラスター分析の種類

データ分析の手法として、複数のデータをその特徴に基づいてグループ分けする手法、クラスター分析があります。クラスター分析は大きく分けて二つの種類があり、それぞれ異なる特性と利点を持っています。一つは階層クラスター分析、もう一つは非階層クラスター分析です。
階層クラスター分析は、似ているデータ同士を段階的にまとめていく手法です。分析対象のデータそれぞれを個別のまとまりとして開始し、最も似ている二つのまとまりを結合します。この結合操作を、全てのデータが一つの大きなまとまりになるまで繰り返します。この一連のまとまり作りの過程は、樹形図と呼ばれる木の枝のような図で表現できます。樹形図を用いることで、データ同士の関係性を視覚的に把握することが容易になります。どの段階でどのデータがまとまりを作るのかを確認できるため、データの構造や特徴を探索的に分析する際に役立ちます。
一方、非階層クラスター分析は、あらかじめいくつのまとまりを作るかを決めておき、それぞれのデータがどのまとまりに属するかを割り当てる手法です。よく用いられる手法の一つに、k-means法があります。この手法では、まず最初に指定した数の中心点を無作為に配置します。そして、各データは最も近い中心点のまとまりに割り当てられます。その後、各まとまりに属するデータの平均値を新たな中心点として再計算し、再度データの割り当てを行います。この処理を繰り返すことで、データの配置が安定し、最適なまとまりが形成されます。階層クラスター分析と比べて計算量が少ないため、大量のデータ分析に適しています。
このように、階層クラスター分析と非階層クラスター分析は異なる特徴を持つため、分析の目的やデータの特性に合わせて適切な手法を選択することが重要です。
| 項目 | 階層クラスター分析 | 非階層クラスター分析 |
|---|---|---|
| 手法 | 似ているデータ同士を段階的にまとめていく | あらかじめいくつのまとまりを作るかを決めておき、それぞれのデータがどのまとまりに属するかを割り当てる |
| 過程 | 全てのデータが一つのまとまりになるまで結合を繰り返す | 指定した数の初期中心点を配置し、データの割り当てと中心点の再計算を繰り返す |
| 表現 | 樹形図 | 散布図など |
| 利点 | データ同士の関係性を視覚的に把握しやすい、データの構造や特徴を探索的に分析できる | 計算量が少ないため、大量のデータ分析に適している |
| 代表例 | – | k-means法 |
階層クラスター分析

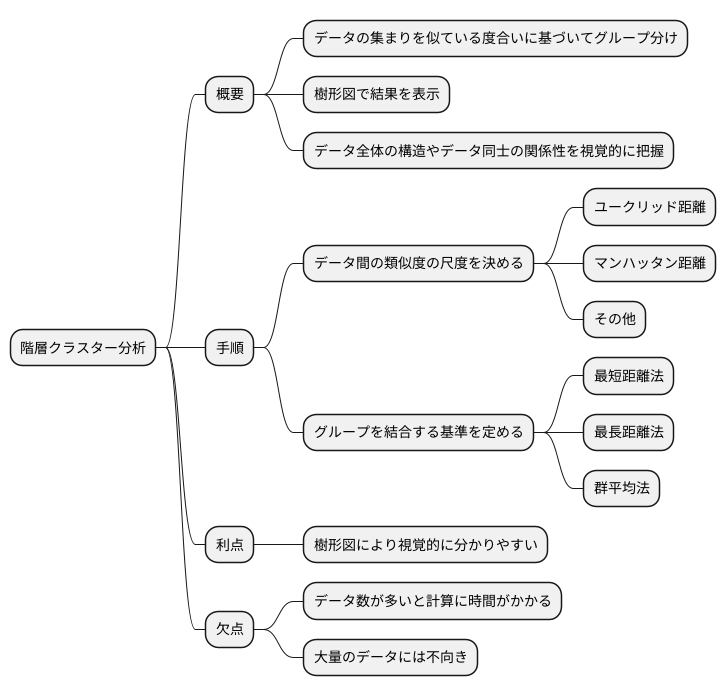
階層クラスター分析とは、対象となるデータの集まりを、互いの似ている度合いに基づいて、段階的にグループ分けしていく分析手法です。これは、まるで木の枝のように、小さなグループが集まって大きなグループを形成していく様子を図示化できることから、樹形図と呼ばれる図で結果を表します。この樹形図を見ることで、データ全体の構造やデータ同士の関係性を視覚的に把握することができます。
階層クラスター分析を行う際には、まずデータ間の似ている度合いを測る尺度を決めなくてはなりません。例えば、データが数値で表されている場合、二点間の距離を測るユークリッド距離やマンハッタン距離などがよく使われます。ユークリッド距離は、いわゆる普通の距離のことで、マンハッタン距離は碁盤の目のような道筋に沿って測る距離のことです。他にも、データの種類や特性に応じて様々な尺度を使い分ける必要があります。
次に、グループを結合する際の基準を定めます。例えば、二つのグループを結合する際に、それぞれのグループに属するデータの中で最も距離が近いもの同士の距離を基準とする「最短距離法」、最も遠いもの同士の距離を基準とする「最長距離法」、また、グループ内の全データ間の平均距離を用いる「群平均法」などがあります。どの基準を用いるかによって、出来上がるグループの形や大きさが変化します。そのため、分析の目的やデータの特性に合わせて適切な基準を選ぶことが重要です。
階層クラスター分析は、樹形図によって視覚的に分かりやすい結果を得られるという大きな利点があります。しかし、扱うデータの数が増えると、計算に時間がかかり、コンピュータへの負担も大きくなるという欠点も持っています。そのため、大量のデータを扱う場合には、階層クラスター分析はあまり適していません。そのような場合は、他の分析手法を検討する必要があります。
非階層クラスター分析

非階層クラスター分析とは、データをいくつかの集団(クラスター)に分類する手法で、階層的な構造を持たずに、あらかじめいくつの集団に分けるかを指定する必要があります。この手法の中で、最もよく知られているのがk-means法です。k-means法は、指定された数の集団の中心(セントロイド)をランダムに配置するところから始まります。次に、それぞれのデータが、どのセントロイドに最も近いかを計算し、最も近いセントロイドに属する集団に割り当てます。そして、各集団に属するデータの平均値を計算し、それを新たなセントロイドとして更新します。この割り当てと更新の作業を、セントロイドの位置が変化しなくなるまで繰り返すことで、最終的な集団分けが得られます。
k-means法は、計算が速く、大量のデータを扱うことができるという利点があります。しかし、最初にセントロイドをランダムに配置するため、分析を行うたびに結果が異なる可能性があるという欠点も持っています。また、極端に外れた値を持つデータ(外れ値)の影響を受けやすいという問題点もあります。
最適な集団の数を決めるためには、いくつかの方法があります。例えば、エルボー法では、集団の数を変えながら分析を行い、それぞれの集団内でのデータのばらつきを計算します。そして、ばらつきの減少が緩やかになる手前の集団の数を最適な数として選択します。シルエット分析では、各データが自身の集団にどれだけうまく所属しているかを数値化し、その平均値を指標として集団の数を評価します。
k-means法の欠点を補うために、改良された手法も開発されています。例えば、k-medoids法は、セントロイドとして実際のデータ点を使用することで、外れ値の影響を軽減します。また、k-means++は、初期セントロイドの配置方法を工夫することで、結果の安定性を向上させています。
非階層クラスター分析は、様々な分野で活用されています。例えば、顧客を購買行動などに応じてグループ分けする顧客セグメンテーションや、画像認識における画像の分類などに利用されています。
| 手法 | 説明 | 利点 | 欠点 | 対策 | 最適化手法 |
|---|---|---|---|---|---|
| k-means法 | 指定された数の集団の中心(セントロイド)をランダムに配置し、データとの距離に基づいて集団を形成。セントロイドの更新を繰り返す。 | 計算が速く、大量のデータを扱える。 | 結果が不安定、外れ値の影響を受けやすい。 | k-medoids法、k-means++ | エルボー法、シルエット分析 |
非階層クラスター分析
- データを階層構造を持たない複数の集団に分類
- あらかじめ集団の数を指定
- 活用例:顧客セグメンテーション、画像認識
まとめ

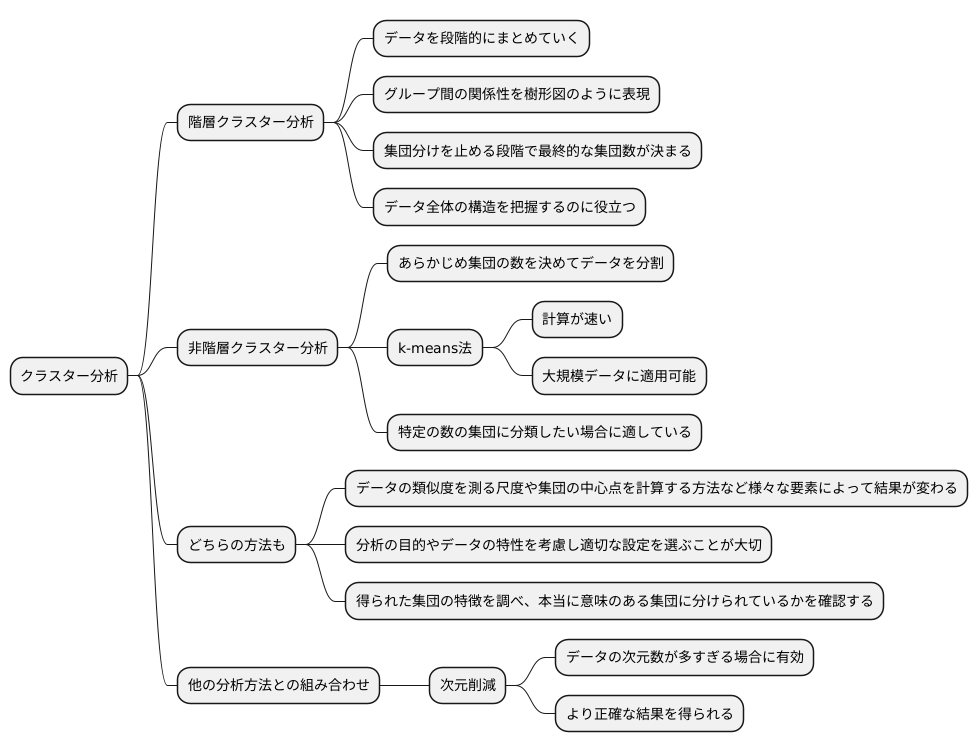
データの中に隠れた集団を見つける方法であるクラスター分析は、様々な分野で役立つ強力な道具です。大きく分けて、階層クラスター分析と非階層クラスター分析という二つの種類があります。この二つの方法は、それぞれ異なる性質と利点を持っているため、分析の目的に合わせて適切な方を選ぶことが重要です。
階層クラスター分析は、データを段階的にまとめていくことで、グループ間の関係性を樹形図のように表現します。似たもの同士が次第に大きな集団を形成していく様子が視覚的に分かりやすいのが特徴です。どの段階で集団分けを止めるかによって、最終的な集団の数が決まります。この方法は、データ全体の構造を把握するのに役立ちます。
一方、非階層クラスター分析は、あらかじめ集団の数を決めておき、データをその数の集団に分割します。代表的な手法であるk-means法は、計算が比較的速く、大規模なデータにも適用できるため、広く利用されています。この方法は、特定の数の集団にデータを分類したい場合に適しています。
どちらの方法も、データの類似度を測る尺度や、集団の中心点を計算する方法など、様々な要素によって結果が変わるため、分析の目的やデータの特性を考慮して適切な設定を選ぶことが大切です。分析結果を正しく理解するためには、得られた集団の特徴を詳しく調べ、本当に意味のある集団に分けられているかを確認する必要があります。
さらに、クラスター分析は他の分析方法と組み合わせることで、より効果を発揮することもあります。例えば、データの次元数が多すぎる場合は、あらかじめ次元削減の手法を用いてデータの数を減らしてからクラスター分析を行うことで、より正確な結果が得られることがあります。
このように、クラスター分析は、分析の目的を明確にし、適切な手法と設定を選ぶことで、様々な問題解決に役立つ手法です。データを分析し、隠れた規則性や関係性を見つけ出すことで、事業の改善や研究の進展に貢献することができます。