勝負に勝つための必勝法:ミニマックス法

AIを知りたい
先生、「ミニマックス法」って、結局どういうものなんですか?

AIエンジニア
そうですね、簡単に言うと、ゲームで自分が一番有利になるように、相手が一番不利になるように考える方法です。たとえば、オセロを想像してみてください。

AIを知りたい
オセロですか?

AIエンジニア
はい。自分が白を置くとします。ミニマックス法を使うと、白を置くことで自分の石を最大限に増やしつつ、同時に相手の黒石を最小限にする場所を探します。相手も同様に、黒石を増やしつつ白石を減らす場所を探します。このように、お互いが自分の利益を最大化し、相手の利益を最小化するように行動を決める方法がミニマックス法です。
Mini-Max法とは。
コンピューターゲームなどでよく使われる『ミニマックス法』という技術について説明します。この方法は、ゲームで自分が指す番には、自分に一番有利になるように、つまり点数が一番高くなるように指します。そして、相手が指す番には、相手に一番不利になるように、つまり相手の点数が一番低くなるように考えるとされています。このように、自分の番では最高点(最大)、相手の番では最低点(最小)を目指して考えることから、『ミニマックス法』と名付けられました。
ミニマックス法とは

ミニマックス法は、二人で勝負を決めるタイプのゲームで、最適な作戦を考えるための方法です。このタイプのゲームは、チェスや将棋、オセロのように、必ず勝敗が決まり、運の要素はなく、お互いの手の内がすべて見えているという特徴があります。
ミニマックス法では、ゲームの木と呼ばれる図を使って、これから起こりうるゲームのすべての手順を調べます。この木は、枝分かれした図で、それぞれの分岐点でどちらかの相手が手を選び、最終的に葉の部分で勝敗が決まります。ミニマックス法は、この木全体を調べ、自分の得点が最大に、相手の得点が最小になるような手を探します。
たとえば、自分が次に手を打つ場面を考えてみましょう。可能な手がいくつかあるとします。それぞれの手に対応する枝をたどっていくと、相手の番になります。相手も、自分の得点が最大になるように手を選びます。これを繰り返して、最終的に葉の部分、つまりゲームの終わりまでたどります。それぞれの葉には、自分の得点が決まっています。
ここで、相手は自分の得点を最小にするように手を選ぶと考えます。つまり、自分が次に選べる手それぞれについて、相手が最も自分に不利な手を選んだ場合の自分の得点を考えます。そして、それらの得点の中で最大のものを選ぶのが、ミニマックス法です。
このように、ミニマックス法は、相手が最善を尽くすことを前提に、自分が確実に得られる最大の得点を得るための作戦を立てる方法です。ただし、ゲームによっては、ゲームの木が非常に大きくなり、すべての展開を調べるのが現実的に不可能な場合もあります。そのような場合は、探索の深さを制限したり、枝刈りなどの工夫が必要になります。
ゲームの木と探索

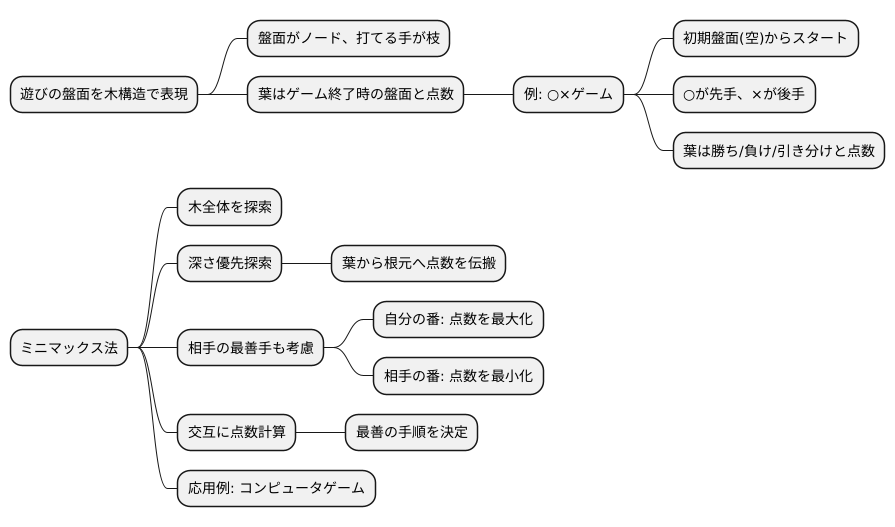
遊びの盤面を木の形に表して、どの順番で遊ぶのが一番良いかを考える方法について説明します。この木は、今の盤面から始め、打てる手を枝のように広げていきます。それぞれの枝の先には、その手を打った後の盤面があります。そこからまた、打てる手を広げ、枝分かれを繰り返します。木の葉っぱにあたる一番端の部分は、遊びが終わった状態、つまり勝ち負けが決まった盤面と、その時の点数です。
例えば、○×ゲームを思い浮かべてみてください。最初の盤面は空っぽで、そこから○が最初にどこに置くかで枝分かれが始まり、次に×がどこに置くかでさらに枝分かれしていきます。最終的には、○か×のどちらかが勝ちか、引き分けで遊びが終わります。それぞれの終わりには、勝ちならプラスの点数、負けならマイナスの点数、引き分けならゼロといったように、点数がつきます。
この木全体を調べる方法を「ミニマックス法」と言います。ミニマックス法は、木の根元、つまり最初の盤面から、葉っぱの先まで順番に調べていきます。そして、それぞれの盤面で、自分にとって一番良い点数を見つけ出します。この調べ方は、「深さ優先探索」と呼ばれ、一番深いところ、つまり葉っぱの部分から根元に向かって点数を伝えていきます。
ミニマックス法では、相手も自分と同じように、一番良い手を打つと仮定します。つまり、自分の番では点数が大きくなるように手を考え、相手の番では点数が小さくなるように相手が手を打つと考えます。このように、交互に立場を入れ替えて、一番深いところから点数を伝えていくことで、どの順番で手を打てば一番良い点数が得られるかを計算することができます。この方法は、色々な遊びに応用でき、コンピュータが人間と対戦するゲームなどでも使われています。
評価関数と深さ

勝負事が終わった後の盤面、つまりどちらが勝ったかがはっきりした状態を「末端」と呼びます。この末端には、それぞれ得点がついています。しかし、実際の勝負では、この末端の状態すべてを調べることは難しいです。なぜなら、考えられる盤面の組み合わせは膨大で、すべてを計算しようとすると途方もない時間がかかってしまうからです。
そこで、ある程度の深さまでしか盤面を読まないようにします。この深さの限界を「探索の深さ」と呼びます。たとえば、「3手先まで読む」といった場合、3手が探索の深さとなります。探索の深さの手前まで来たら、盤面を評価関数を使って評価します。評価関数は、現在の盤面がどれくらい有利かを数値で表すものです。たとえば、将棋であれば、「自分の駒の価値の合計 - 相手の駒の価値の合計」のような計算式で盤面の有利不利を数値化できます。この評価関数の値を、末端の得点の代わりに使います。
この探索の深さは、計算にかかる時間と、読みの正確さ、両方に影響を与えます。深く読めば読むほど、より正確な盤面の評価ができます。しかし、深く読むほど計算量が増え、時間もかかります。浅く読む場合は、すぐに計算は終わりますが、正確さは下がります。たとえば、3手先まで読むのと、5手先まで読むのでは、5手先まで読んだ方が正確な判断ができますが、計算時間は5手先まで読んだ方が長くなります。
適切な探索の深さは、扱う勝負事の種類や、使える計算時間によって変わります。複雑な勝負事ほど、深く読む必要があります。また、持ち時間が長い場合は深く読むことができますが、持ち時間が短い場合は、深く読むと時間が足りなくなる可能性があります。そのため、勝負事の種類や状況に応じて、適切な深さを選ぶことが重要です。
| 項目 | 説明 |
|---|---|
| 末端 | 勝負事が終わった後の盤面。得点がついている。 |
| 探索の深さ | 盤面を読む深さの限界(例:3手先まで読む)。 |
| 評価関数 | 探索の深さの手前で盤面を評価する関数。盤面の有利不利を数値化。 |
| 探索の深さと計算時間/正確さの関係 | 深いほど正確だが時間がかかる。浅いほど速いが正確さは下がる。 |
| 適切な探索の深さ | 勝負事の種類や使える計算時間によって変わる。 |
最大化と最小化

「最大化と最小化」という名前は、まさにこの方法の本質を表しています。ゲームにおいて、自分が有利になるように、つまり自分の得点をなるべく大きくするのが「最大化」です。反対に、相手が有利にならないように、つまり相手の得点をなるべく小さくするのが「最小化」です。この二つの考え方を交互に繰り返すことで、最良の手を見つけるのがこの方法です。
自分の番では、あらゆる選択肢の中から、自分が最も高い得点を得られる手を選びます。もちろん、相手も自分の番で同じように最良の手を選ぶと想定します。相手は、私たちの得点が最も低くなるように手を選んでくるでしょう。つまり、相手は「最小化」を目指します。
このように、自分が「最大化」を、相手が「最小化」を行うことを交互に繰り返しながら、何手か先まで読みます。たとえば、自分が次に指せる全ての手を考え、そのそれぞれに対して、相手が次に指せる全ての手を考えます。さらに、そのそれぞれに対して、自分が次に指せる全ての手を考え…というように、できる限り先まで読み進めます。もちろん、あまりに先まで読むと計算量が膨大になるので、実際にはある程度で打ち切ります。
そして、この読みの中で、自分が最終的に得られるであろう得点の中で、最も高い得点を選びます。同時に、相手が最終的に私たちに与えるであろう得点の中で、最も低い得点も考慮します。つまり、相手が最善を尽くしてきた場合でも、自分が確実に得られる最高得点を目指すのです。これが「ミニマックス法」と呼ばれる所以です。
このようにして、お互いが最善の手を打つという前提のもとで、最良の手順を見つけ出すことができるのです。この方法は、将棋や囲碁のような、二人で対戦するゲームでよく使われています。
アルファベータ法

勝負を決める場面で、どのように最善手を選ぶか、という問いは古くから考えられてきました。その有効な手法の一つに、ミニマックス法というものがあります。ミニマックス法は、ゲームの状況を木構造で表現し、自分の番では最大の利益を得るように、相手の番では自分が最小の利益になるように行動を選択する、という考え方です。しかし、この方法は、ゲームの複雑さに比例して計算量が爆発的に増えてしまう、という欠点がありました。そこで、ミニマックス法の計算を効率化する手法として、アルファベータ法が考案されました。
アルファベータ法は、ミニマックス法と同じく、ゲームの状況を木構造で表現し、探索を行います。しかし、アルファベータ法は、探索の途中で明らかに最適ではない分岐を途中で打ち切る、という工夫を加えています。具体的には、探索中に「アルファ」と「ベータ」と呼ばれる二つの値を更新していきます。アルファは、探索中に見つかった自分にとっての利益の最小値を、ベータは自分にとっての損失の最大値を表します。そして、ある分岐を探索した結果、その分岐での利益がアルファよりも小さい、あるいは損失がベータよりも大きいとわかった時点で、その分岐以降の探索を打ち切ります。なぜなら、その分岐は、既に探索済みの他の分岐よりも悪い結果をもたらすことが明らかだからです。
例えて言うなら、宝探しをしていると想像してみてください。複数の宝箱があり、それぞれに異なる価値の宝が入っています。アルファは、既に開けた宝箱の中身で最も価値の低い宝の価値、ベータは、これまでに見つけた宝箱の中で、鍵を開けるのに最も多くの時間が必要な宝箱を開けるのにかかった時間だとします。新しい宝箱を見つけた時、もしその宝箱の鍵を開けるのに、既に開けた宝箱の中の最も価値の低い宝よりも多くの時間が必要だとわかったら、その宝箱を開けるのはやめます。なぜなら、既に開けた宝箱の中に、もっと短い時間で開けられる上に、より価値の高い宝が入っている宝箱があるからです。アルファベータ法は、このようにして不要な探索を省き、ミニマックス法よりも高速に最善手を見つけることを可能にします。

実際のゲームへの応用

勝負が先まで見通せるゲーム、例えば、順番に指す盤面を使ったゲームなどで、ミニマックス法は役立ちます。将棋や囲碁、チェスといった昔からあるゲームだけでなく、オセロや五目並べといった比較的簡単なゲームにも使えます。また、テレビゲームやスマホゲームなど画面の中のゲームの対戦相手を作るのにも、この考え方は使われています。
ミニマックス法は、勝ち負けのはっきりしているゲームで力を発揮します。この方法は、自分が一番良い手を選び、相手は自分にとって一番悪い手を選ぶという前提で、先々まで盤面の状態を予測します。たとえば、三手先まで読むとすると、自分が指して、相手が指して、自分が指した時の盤面の状態を考えて、一番有利になるように最初の指し手を決めます。
しかしながら、ミニマックス法をそのまま複雑なゲームに使うのは難しい場合があります。なぜなら、ゲームが複雑になればなるほど、盤面の状態の数がとても多くなってしまうからです。例えば、将棋の場合、一手ごとに可能な指し手の数は非常に多く、先々まで読むと膨大な数の盤面を考えなければなりません。もし全ての盤面を考えると、計算にとても時間がかかってしまいます。
そこで、読む手数を制限したり、盤面の状態の良し悪しを評価する仕組みを工夫したりすることで、計算の量を減らしています。読む手数を制限するとは、例えば三手先までしか読まないようにするということです。盤面の状態の良し悪しを評価する仕組みを工夫するとは、例えば、将棋であれば、駒の数や位置から点数をつけ、点数の高い盤面が有利な盤面だと判断するということです。これらの工夫によって、現実的な時間内でゲームを進めることができます。
ミニマックス法は、ゲームの対戦相手を作るための重要な技術の一つです。この技術を使うことで、強いコンピューターの対戦相手を作ることができます。
| 項目 | 内容 |
|---|---|
| ミニマックス法の適用範囲 | 順番に指す盤面を使ったゲーム(例: 将棋、囲碁、チェス、オセロ、五目並べ、テレビゲーム、スマホゲーム) |
| ミニマックス法の原理 | 自分が最良の手、相手が最悪の手を選ぶと仮定し、先々まで盤面を予測。例:三手先まで読む場合、自分が指し、相手が指し、自分が指した後の盤面から最良の初手を決定 |
| ミニマックス法の課題 | 複雑なゲームへの適用困難。盤面の状態数が膨大になり、計算に時間がかかる。 |
| ミニマックス法の対策 | 読む手数の制限、盤面評価の工夫。 |
| 対策の具体例 | 読む手数の制限:三手先まで読む。盤面評価:駒の数や位置から点数をつける。 |
| ミニマックス法のメリット | 強いコンピュータ対戦相手の作成が可能。 |
