移動平均の基礎と応用

AIを知りたい
先生、「EMA」って金融や統計の分野でよく聞くんですけど、どんなものなんですか?

AIエンジニア
いい質問だね。「EMA」は「指数平滑移動平均」の略で、簡単に言うと、最近のデータに重みを付けて平均を出す方法だよ。過去に遡るほど、データの影響度がだんだん小さくなるんだ。

AIを知りたい
最近のデータに重みを付けるって、どういうことですか?

AIエンジニア
例えば、今日の株価に0.2、昨日の株価に0.16、…というように、新しいデータほど大きな値を掛けて平均を計算するんだよ。そうすることで、最近の値動きをより反映した平均値が得られるんだ。
EMAとは。
人工知能に関わる言葉である「イーエムエー」について説明します。これは、お金の分野や数学、統計学、機械学習で使われる用語で、データを滑らかに繋げることで、データの傾向や変化を分かりやすくする手法です。
移動平均とは

移動平均とは、ある一定の期間の値の平均を次々と算出していくことで、変動の激しいデータの傾向を掴みやすくする手法です。日々の気温や株価、為替の変動など、時間とともに変化するデータによく使われます。
例えば、過去5日間の株価の平均を毎日計算するとします。1日目から5日目までの株価の平均を計算し、次に2日目から6日目までの株価の平均を計算します。これを毎日繰り返すことで、日々の小さな値動きに惑わされず、株価の大きな流れや方向性を知ることができます。これが移動平均の基本的な考え方です。
移動平均には、いくつか種類があります。単純移動平均は、期間内の値を全て同じ重みで平均する、最も基本的な方法です。一方で、加重移動平均は、期間内の新しい値により大きな重みを与え、古い値の影響を少なくする方法です。最近の値動きを重視したい場合に有効です。さらに、指数移動平均は、直近の値により大きな重みを付け、過去に遡るほど重みを指数関数的に減らしていく方法です。急激な変化にも素早く反応することができます。
どの移動平均を使うかは、分析の目的によって異なります。短期的な変動を捉えたい場合は短い期間の移動平均を、長期的な傾向を掴みたい場合は長い期間の移動平均を用います。移動平均の長所は、計算が簡単で理解しやすい点です。しかし、過去のデータに基づいて計算されるため、将来の値動きを確実に予測できるわけではありません。移動平均は、単独で使うだけでなく、他の分析手法と組み合わせて使うことで、より効果を発揮します。例えば、移動平均を組み合わせることで、売買の時期を判断する材料としたり、将来の値動きを予測する助けにしたりすることができます。
| 移動平均の種類 | 計算方法 | 特徴 | 用途 |
|---|---|---|---|
| 単純移動平均 | 期間内の値を全て同じ重みで平均 | 最も基本的な方法 | – |
| 加重移動平均 | 期間内の新しい値により大きな重みを与え、古い値の影響を少なく | 最近の値動きを重視したい場合に有効 | – |
| 指数移動平均 | 直近の値により大きな重みを付け、過去に遡るほど重みを指数関数的に減らす | 急激な変化にも素早く反応 | – |
移動平均は、一定期間の値の平均を次々と算出することで、データの傾向を掴みやすくする手法です。期間の長さによって、短期的な変動または長期的な傾向を分析できます。過去のデータに基づいて計算されるため、未来予測は確実ではありません。他の分析手法と組み合わせて使うことで効果を発揮します。
指数移動平均の特徴

指数移動平均は、値動きを滑らかに示す線を描くための計算方法の一つです。これは、過去の値動きも考慮しつつ、新しい値動きをより重視して平均値を算出する方法です。直近のデータの影響が大きいため、市場の動きに素早く反応することができます。まるで、水に浮かぶ木の葉のように、市場の小さな波にも揺らぎます。
例えば、10日間の指数移動平均を計算する場合を考えてみましょう。この計算方法では、今日一番新しい値動きを最も重視し、昨日の値動きは少し軽く、おとといの値動きはもっと軽く、といった具合に、過去にさかのぼるほど値動きの影響度を軽くしていきます。これは、古い情報よりも新しい情報の方が今の市場をよりよく表していると考えるからです。
一方、単純移動平均という別の計算方法では、10日間すべての値動きを同じ重さで扱います。これは、過去の値動きも現在の値動きも同じように重要だと考えるからです。そのため、単純移動平均は指数移動平均に比べて市場の変化への反応が遅くなります。まるで、大きな船のように、小さな波には揺らぎません。
指数移動平均は、市場の小さな変化を素早く捉えることができるため、短期的な売買判断に役立ちます。ただし、市場が急激に変動すると、その影響を受けやすいという弱点もあります。小さな木の葉は、強い風にも大きく揺られてしまいます。
より精度の高い分析を行うためには、他の分析方法と組み合わせて使うことが効果的です。例えば、市場の大きな流れを掴むために単純移動平均を使い、小さな変化を捉えるために指数移動平均を使う、といった方法が考えられます。まるで、大きな船で航路を決めつつ、小さなボートで周囲の状況を確認するようなものです。
| 項目 | 指数移動平均 | 単純移動平均 |
|---|---|---|
| データの重み付け | 新しいデータほど重みを大きくする | すべてのデータを同じ重みで扱う |
| 市場の変化への反応 | 速い (木の葉) | 遅い (大きな船) |
| メリット | 短期的な売買判断に役立つ | 市場の大きな流れを掴むのに役立つ |
| デメリット | 急激な変動の影響を受けやすい | 変化への反応が遅い |
| 使用例 | 短期的な売買判断 | 長期的なトレンド分析 |
計算方法

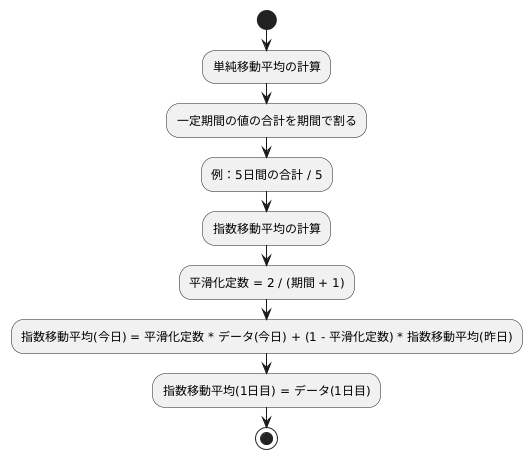
計算方法は、まず単純移動平均を計算することから始めます。単純移動平均とは、一定期間の値の合計を期間で割った値のことです。例えば、5日間の単純移動平均を求める場合、5日間の値を合計し、5で割ります。この単純移動平均を基に、指数移動平均を求めます。
指数移動平均は、過去のデータの影響を次第に小さくするように計算します。具体的には、平滑化定数と呼ばれる値を用いて、過去のデータの影響を調整します。この平滑化定数は、期間が長くなるほど小さくなります。つまり、長い期間の指数移動平均を計算する場合、過去のデータの影響は小さくなります。逆に、短い期間の指数移動平均を計算する場合、過去のデータの影響は大きくなります。
指数移動平均の計算式は、以下のようになります。今日の指数移動平均の値は、今日のデータに平滑化定数を掛けた値と、昨日の指数移動平均の値に(1−平滑化定数)を掛けた値を足し合わせて求めます。式で表すと、指数移動平均(今日)=平滑化定数×データ(今日)+(1−平滑化定数)×指数移動平均(昨日)となります。
平滑化定数は、一般的に2÷(期間+1)で計算します。例えば、期間が5日間の指数移動平均の場合、平滑化定数は2÷(5+1)=0.333となります。期間が20日間の指数移動平均の場合、平滑化定数は2÷(20+1)=約0.095となります。このように、期間が長くなるほど、平滑化定数は小さくなります。
最初の日の指数移動平均の値は、最初の日のデータの値と同じ値とします。2日目以降は、上記の計算式を使って指数移動平均の値を求めます。こうして、過去のデータの影響を徐々に小さくしながら、最新のデータの値を反映した移動平均を計算することができます。これにより、直近の値を重視しつつ、長期的な傾向も把握することが可能となります。
金融での活用例

お金の世界では、指数平滑移動平均(略して移動平均)は、値動きの分析に欠かせない道具となっています。これは、過去の値動きを滑らかに繋いで、現在の傾向を捉えるのに役立ちます。
例えば、短期の移動平均と長期の移動平均を組み合わせることで、売買の機会を見つけることができます。短期の移動平均が長期の移動平均を上回った時、これは買いの合図と見なされます。逆に、短期の移動平均が長期の移動平均を下回った時、これは売りの合図と見なされます。この方法は、まるで金色の線が交差する様子や、死を連想させる黒い線が交差する様子から、それぞれ「黄金交叉」「死の交叉」と呼ばれ、多くの投資家に利用されています。
移動平均は、それ自体で使うだけでなく、他の分析方法と組み合わせることで、より効果的な分析ができます。例えば、移動平均乖離率は、異なる期間の移動平均の差を計算することで、現在の値動きが平均からどれくらい離れているかを示す指標です。この指標を使うことで、値動きの勢いや変化の兆候を捉えることができます。
移動平均は過去の値動きに基づいて計算されるため、未来の値動きを完全に予測することはできません。市場は様々な要因に影響されるため、移動平均だけに頼らず、他の情報も考慮して、市場全体の様子を理解することが大切です。また、投資には常にリスクが伴うため、適切なリスク管理を行うことも重要です。未来を確実に予測する魔法の杖はありませんが、様々な道具を組み合わせて使うことで、より確かな判断ができます。
| 移動平均 | 説明 | 使い方 | 注意点 |
|---|---|---|---|
| 定義 | 過去の値動きを滑らかに繋いで、現在の傾向を捉えるための分析手法 | 短期・長期の移動平均を組み合わせることで売買の機会を捉える | 過去の値動きに基づいて計算されるため、未来の値動きを完全に予測することはできない |
| 黄金交叉 | 短期の移動平均が長期の移動平均を上回った時。買いの合図。 | 売買シグナル | 市場は様々な要因に影響されるため、移動平均だけに頼らず、他の情報も考慮する必要がある |
| 死の交叉 | 短期の移動平均が長期の移動平均を下回った時。売りの合図。 | 売買シグナル | 投資には常にリスクが伴うため、適切なリスク管理を行うことが重要 |
| 移動平均乖離率 | 異なる期間の移動平均の差を計算することで、現在の値動きが平均からどれくらい離れているかを示す指標 | 値動きの勢いや変化の兆候を捉える | – |
機械学習での応用

機械学習の世界では、移動平均の計算は、時系列データの分析によく使われています。刻一刻と変わるデータの特徴を捉え、より正確な予測や判断を行うために役立っています。
例えば、株価の動きを予測するモデルを考えてみましょう。株価は日々変動し、細かい上下動を繰り返すため、予測が難しくなります。そこで、移動平均を使うことで、短期間の変動を取り除き、全体的な傾向を捉えることができます。滑らかなデータとして扱うことで、予測モデルの精度向上が期待できます。
また、試行錯誤を通じて学習を進める強化学習という分野でも、移動平均は重要な役割を果たします。学習過程では、得られる報酬が大きく変動することがあります。そのため、報酬の移動平均を計算することで、学習の進み具合を安定させ、より効率的に学習を進めることができます。
さらに、普段とは異なる異常な状態を検出する異常検知という分野でも、移動平均は活用されています。過去のデータから正常な状態におけるデータの基準値を移動平均によって求めます。そして、現在のデータがこの基準値から大きく外れている場合、異常と判断することができます。
このように、移動平均は、機械学習の様々な場面で利用されています。近年では、深層学習と呼ばれる複雑なモデルと組み合わせることで、さらに高度な時系列データ分析が可能になりつつあります。大量のデータから複雑なパターンを学習し、これまで以上に精度の高い予測や分析を行うことが期待されています。
| 分野 | 移動平均の役割 |
|---|---|
| 株価予測 | 細かい変動を取り除き、全体的な傾向を捉えることで予測精度を向上 |
| 強化学習 | 報酬の変動を滑らかにし、学習の進み具合を安定させ、効率的な学習を実現 |
| 異常検知 | 正常な状態の基準値を算出し、異常な値を検出 |
| 深層学習 | 複雑な時系列データ分析を可能にし、高精度な予測や分析を実現 |
長所と短所

移動平均線には、単純移動平均線と指数移動平均線といった種類があります。このうち、指数移動平均線は、英語でExponential Moving Averageといい、略してEMAと呼ばれています。EMAは、直近の価格データに大きな比重を置いて計算されるため、最近の市場の動きをより敏感に反映するという特徴を持っています。
EMAの最大の強みは、市場のトレンドの変化に素早く対応できる点にあります。短期的な売買を行う場合、市場の動きをいち早く捉えることが重要となるため、EMAは短期売買の戦略において非常に役立ちます。また、EMAは計算方法が比較的単純で、理解しやすいという利点もあります。複雑な計算式を理解する必要がないため、初心者でも容易に利用できます。
一方で、EMAは価格の急激な変動に過敏に反応してしまうという弱点もあります。市場においては、一時的な出来事によって価格が大きく動くことがありますが、EMAはこのような一時的な変動に影響を受けやすく、誤った売買の指示を出してしまう可能性があります。いわゆる「だまし」に引っかかりやすい指標とも言えます。また、EMAは過去のデータに基づいて計算されるため、未来の価格を確実に予測できるわけではありません。特に、市場の環境が大きく変化した場合、EMAの予測精度は低下する傾向にあります。
そのため、EMAだけで売買の判断をするのではなく、他の指標も併用して、市場全体の状況を総合的に判断することが重要です。例えば、出来高や他のテクニカル指標と組み合わせることで、より精度の高い分析を行うことができます。さまざまな情報を組み合わせて使うことで、リスクを抑えながら、より効果的な投資判断を行うことができるでしょう。
| 項目 | 内容 |
|---|---|
| 種類 | 単純移動平均線、指数移動平均線(EMA) |
| EMAの特徴 | 直近の価格データに大きな比重を置いて計算、最近の市場の動きをより敏感に反映 |
| EMAの強み | 市場のトレンドの変化に素早く対応、計算方法が比較的単純で理解しやすい |
| EMAの弱点 | 価格の急激な変動に過敏に反応(だまし)、過去のデータに基づいて計算されるため未来の価格を確実に予測できない、市場環境の変化で予測精度が低下 |
| EMA利用の際の注意点 | 他の指標と併用(出来高、他のテクニカル指標など)し、市場全体の状況を総合的に判断 |
