外れ値に強い!トリム平均入門

AIを知りたい
先生、「トリム平均」って、どういう意味ですか?よくわからないです。

AIエンジニア
トリム平均は、データを扱うとき、一番大きい値や一番小さい値をいくつか除外してから平均を出す方法だよ。たとえば、10個のデータがあったとして、最大値と最小値を除いた8個のデータで平均を求めるといった具合だね。

AIを知りたい
どうして、最大値や最小値を除外する必要があるのですか?

AIエンジニア
すごく大きい値や小さい値があると、普通の平均値がそれらの値に引っ張られてしまうことがあるんだ。そうすると、データ全体の様子を正しく表せなくなる場合がある。だから、極端な値の影響を受けないように、トリム平均を使うんだよ。
トリム平均とは。
『調整平均』という人工知能で使われる言葉について説明します。調整平均は、数学や統計学、機械学習の分野で用いられます。まず、データ全体から一部のデータを取り除きます。そして、残ったデータを使って平均値を計算します。この平均値のことを調整平均といいます。ちなみに、普通の平均値は、全てのデータの合計をデータの数で割って計算します。
トリム平均とは

トリム平均とは、集めた数値から一部の数値を取り除き、残りの数値で平均値を計算する方法です。私たちが普段よく使う平均値は、全ての数値を足し合わせ、その合計を集めた数値の個数で割ることで計算します。これを算術平均と言います。しかし、集めた数値の中に極端に大きな値や小さな値が含まれている場合、算術平均はこれらの極端な値に引っ張られてしまい、データ全体の傾向を正しく表せなくなってしまうことがあります。例えば、10人の仲間の年収を調べた際に、9人が300万円から500万円の年収だったとします。ところが、残りの1人がたまたま大企業の社長で、年収が3億円だったとしましょう。この場合、単純に平均値を計算すると、他の9人の年収が300万円から500万円であるにも関わらず、平均年収は数千万円という大きな値になってしまいます。このような場合、極端な値の影響を取り除き、より実態に近い平均値を求めるためにトリム平均が用いられます。トリム平均では、まず集めた数値を小さい順に並べ替えます。そして、両端から同じ割合の数値を取り除きます。例えば、10個の数値があった場合、両端から10%ずつ、つまり上下から1個ずつの数値を取り除きます。この時、取り除く数値の割合をトリミング率と言います。そして、残った8個の数値を使って平均値を計算します。これがトリム平均です。トリム平均を使うことで、極端に大きな値や小さな値の影響を受けにくく、データ全体の中心的な傾向をより正確に捉えることができます。
| 項目 | 説明 |
|---|---|
| 算術平均 | 全ての数値を足し合わせ、数値の個数で割る。 |
| 算術平均の問題点 | 極端な値に影響を受けやすい。 |
| トリム平均 | 極端な値を取り除いて計算する平均値。 |
| トリム平均の計算方法 | 1. 数値を小さい順に並べ替える。 2. 両端から一定の割合の数値を取り除く。 3. 残りの数値で平均値を計算する。 |
| トリミング率 | 取り除く数値の割合。 |
| トリム平均のメリット | 極端な値の影響を受けにくく、データの中心的な傾向を捉えやすい。 |
| 例 | 10人の年収のうち、9人が300-500万円、1人が3億円の場合、算術平均では高すぎる値になるため、トリム平均が有効。 |
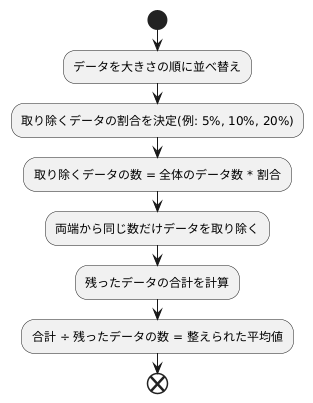
計算方法

計算方法は、まず整理整頓されたデータを作ることから始まります。集めたデータを大きさの順に並べ替えます。小さいものから大きいものへ、またはその逆へと、規則正しく整列させることが大切です。
次に、どのくらいの量のデータを取り除くかを決めます。これは、集めたデータの特徴や、どの程度かけ離れた値が含まれているかによって、自由に決めることができます。例えば、全体の5%、10%、20%など、割合で指定します。取り除くデータの数は、全体のデータの数にこの割合を掛けて計算します。例えば、全部で100個のデータがあり、10%を取り除くと決めた場合は、100に0.1を掛けて10個になります。
両端から同じ数だけデータを取り除くのがポイントです。先ほどの例では、10個のデータを取り除くと決めました。ですので、整列させたデータの小さい方から10個、そして大きい方からも10個、合計20個のデータを取り除きます。
データを取り除いた後は、残ったデータの合計を計算します。全ての値を足し合わせることで、全体の量を求めます。そして、残ったデータの数でこの合計を割ります。これで、整えられた平均値が求まります。この計算方法を使うと、極端に大きな値や小さな値に影響されにくい、より確かな平均値を得ることができます。全体の様子をより正確に捉えることができるのです。
算術平均との違い

普段よく使う平均、つまり全ての数を足してその個数で割る計算方法を算術平均と言います。これは多くの場合、データ全体の様子を捉えるのに役立ちます。例えば、ある学級の生徒全員のテストの点数を足して人数で割れば、学級全体の平均点が分かります。
しかし、極端に高い点数や低い点数、いわゆる外れ値があると、この算術平均は実態を正しく反映しないことがあります。例えば、ほとんどの生徒が60点前後を取っているのに、一人だけ100点を取った生徒がいると、平均点が少し上がってしまい、実際より学級全体の成績が良いように見えてしまいます。反対に、一人だけ0点の生徒がいる場合も、平均点が下がってしまうため、学級全体の成績が悪く見えてしまいます。
このような外れ値の影響を少なくするために用いられるのがトリム平均です。トリム平均では、データ全体を高い順あるいは低い順に並べ、両端の一定の割合のデータを取り除いてから平均を計算します。先ほどの例で言えば、0点や100点を取った生徒の点数を除外してから平均点を計算するようなものです。これにより、極端な値に引っ張られることなく、よりデータの中心部分、つまり大多数の生徒の成績を表す平均値を得ることができます。
ただし、トリム平均は一部のデータを除外してしまうため、データ全体の情報を全て使っているわけではありません。そのため、算術平均とトリム平均のどちらが良いかは、データの性質や分析の目的によって異なります。外れ値の影響が懸念される場合はトリム平均を使う方が良いでしょう。反対に、全てのデータが等しく重要で、外れ値も重要な情報である場合は、算術平均を使うべきです。状況に応じて適切な平均値を使い分けることが大切です。
| 平均の種類 | 計算方法 | 長所 | 短所 | 適切な場面 |
|---|---|---|---|---|
| 算術平均 | 全ての値を足し合わせ、データの個数で割る | データ全体の様子を捉えるのに役立つ | 外れ値の影響を受けやすい | 全てのデータが等しく重要で、外れ値も重要な情報である場合 |
| トリム平均 | データ全体をソートし、両端の一定割合のデータを取り除いてから平均を計算する | 外れ値の影響を受けにくい | 一部のデータを除外するため、データ全体の情報を全て使っていない | 外れ値の影響が懸念される場合 |
活用事例

色々な分野で活用されているトリム平均について、具体的な使い方をいくつか見ていきましょう。スポーツの採点競技では、審査員の出す点数のばらつきを抑え、公平な評価をするためにトリム平均がよく使われます。例えば、フィギュアスケートや体操競技を考えてみましょう。選手の見事な演技に、審査員から高い点数が次々と出される一方で、中には採点に厳しい審査員もいるかもしれません。このような場合、最高点と最低点をいくつか取り除き、残りの点数の平均を計算することで、極端に高い点数や低い点数の影響を減らし、より正確な実力を反映した点数を求めることができます。これがトリム平均の考え方です。
また、経済の動きを数値で表す経済指標を計算する際にも、トリム平均は役に立ちます。例えば、私たちの生活にかかる費用を表す消費者物価指数を考えてみましょう。様々な商品の値段の変化を元に計算されますが、中には天候不順などで価格が大きく変動する商品もあるでしょう。このような商品の価格変動は、一時的なものであり、全体の物価の動きを表す上では邪魔になる場合があります。そこで、価格変動の激しい商品のデータを取り除き、残りの商品の価格変動をもとに消費者物価指数を計算することで、より安定した物価の動きを把握することができるのです。トリム平均は、このように経済の動きを正確に捉えるためにも役立っています。
さらに、製品の品質を一定に保つ品質管理や、いつもと違う動きを見つける異常検知といった分野でも、トリム平均は力を発揮します。製品の品質検査で、何らかの原因で通常と異なる測定値が得られる場合があります。また、機械の稼働状況を監視する際には、センサーの誤作動などで異常値が記録されるかもしれません。このような外れ値が含まれるデータでも、トリム平均を使うことで、外れ値の影響を少なくし、より信頼性の高い分析を行うことができるのです。
| 分野 | 使い方 | 効果 |
|---|---|---|
| スポーツの採点競技 | 審査員の採点の最高点と最低点をいくつか取り除き、残りの点数の平均を計算する | 極端な点数の影響を減らし、公平な評価をする |
| 経済指標の計算 | 価格変動の激しい商品のデータを取り除き、残りの商品の価格変動をもとに計算する | 一時的な変動の影響を抑え、安定した経済の動きを把握する |
| 品質管理・異常検知 | 通常と異なる測定値や異常値を取り除き、残りのデータで分析する | 外れ値の影響を少なくし、信頼性の高い分析を行う |
長所と短所

中央値に似た特徴を持つトリム平均は、データ全体のうち最大値と最小値を一定の割合で取り除いた後に平均値を計算する方法です。この計算方法には、いくつかの利点があります。まず、極端に大きい値や小さい値といった外れ値の影響を受けにくいことが挙げられます。例えば、一部の突出した売り上げ数値が全体の平均を押し上げてしまうような場合、トリム平均を用いることで、より実態に近い平均値を把握することができます。また、計算方法自体が比較的単純で、特別な知識や技術を必要としないため、誰でも簡単に計算できます。
しかし、トリム平均には欠点も存在します。最大の特徴である外れ値の影響を受けにくいという点は、裏を返せば、データの一部を意図的に無視しているということでもあります。つまり、トリム平均はデータセットに含まれる全ての情報を活用しているわけではなく、取り除かれたデータに重要な情報が含まれている可能性も否定できません。さらに、どの程度の割合でデータを取り除くかは、分析を行う人の判断に委ねられます。そのため、分析を行う人によって結果が異なり、客観性に欠けるという側面があります。例えば、10%トリム平均と20%トリム平均では、結果に違いが生じる可能性があります。また、データの数が少ない場合、トリム平均の信頼性が低下する点にも注意が必要です。例えば、10個のデータから20%トリム平均を計算する場合、上下それぞれ1個ずつのデータを取り除くことになり、結果として8個のデータから平均値を計算することになります。この場合、取り除かれたデータの影響が相対的に大きくなり、信頼性が低い結果になってしまう可能性があります。
このように、トリム平均には長所と短所の両方があります。そのため、分析の目的やデータの特性を十分に理解した上で、慎重に利用する必要があります。状況によっては、トリム平均ではなく他の統計量を用いる方が適切な場合もあります。例えば、データ数が少ない場合は中央値を用いたり、外れ値の原因を特定できる場合は、その原因に対処した上で平均値を計算する方が良い結果が得られることもあります。
| 項目 | 内容 |
|---|---|
| 定義 | 最大値と最小値を一定の割合で取り除いた後、残りのデータの平均値を計算する統計量。 |
| 利点 |
|
| 欠点 |
|
| 注意点 | 分析の目的やデータの特性を理解し、トリムする割合を適切に設定する必要がある。場合によっては、中央値などの他の統計量の方が適切。 |
まとめ

データの真ん中あたりを調べたいときによく使われるのが、平均値です。全部の値を足して、値の個数で割ることで求めます。しかし、極端に大きい値や小さい値があると、平均値はその影響を大きく受けてしまいます。例えば、10人のテストの点数を考えてみましょう。9人は60点くらいなのに、1人だけ100点を取ったとします。このとき、平均点は64点になり、大部分の人が取った点数よりも高くなってしまいます。このような極端な値を外れ値と言います。
外れ値の影響を少なくして、より正確にデータの中心を捉える方法として、トリム平均という考え方があります。トリム平均は、データの両端から一定の割合の値を取り除いた後に、残りの値で平均値を計算します。先ほどのテストの例で、両端から1人ずつ、つまり一番高い点数と一番低い点数を除いて平均値を計算すると、より正確な平均点が得られます。これがトリム平均です。
トリム平均は、外れ値の影響を受けにくいので、データの中心的な傾向を捉えるのに役立ちます。しかし、一部のデータは使わないという性質上、データ全体の情報を完全に反映しているとは言えません。どの程度の割合のデータを取り除くかは、データの性質や分析の目的に合わせて適切に決める必要があります。データの数が少ない場合は、トリム平均の信頼性が低くなることがあるので、注意が必要です。他の計算方法と比べてみて、どの方法が一番適しているかを考えることが大切です。うまく使えば、トリム平均はデータ分析の強力な道具になります。
| 項目 | 説明 |
|---|---|
| 平均値 | 全ての値を足し合わせ、値の個数で割ることで求める。外れ値の影響を受けやすい。 |
| 外れ値 | 極端に大きい値や小さい値。平均値に大きな影響を与える。 |
| トリム平均 | データの両端から一定の割合の値を取り除き、残りの値で平均値を計算する。外れ値の影響を受けにくい。 |
| トリム平均のメリット | 外れ値の影響を受けにくいので、データの中心的な傾向を捉えるのに役立つ。 |
| トリム平均のデメリット | データ全体の情報は反映されない。データが少ない場合は信頼性が低くなる。 |
| トリム平均を使う上での注意点 | 取り除くデータの割合は、データの性質や分析の目的に合わせて適切に決める必要がある。他の計算方法と比較し、最適な方法を選択する。 |
